Ratio of the perimeter of Bernoulli's lemniscate to its diameter
Лемниската Бернулли В математике лемнискаты константа ϖ [1] [3] [4] [5] трансцендентная математическая константа, представляющая собой отношение периметра лемнискаты к Бернулли ее диаметру , аналогично определению π ( x 2 + y 2 ) 2 = x 2 − y 2 {\displaystyle (x^{2}+y^{2})^{2}=x^{2}-y^{2}} 2 ϖ . Константа лемниската тесно связана с эллиптическими функциями лемниската и примерно равна 2,62205755. [6] [7] [8] [9] ϖ является рукописным вариантом буквы π ; см. Пи § Вариант пи .
Константа Гаусса , обозначаемая G , равна ϖ / π [10]
Джон Тодд назвал еще две лемнискатные константы: первую лемнискатную константу A = ϖ /2 ≈ 1,3110287771 вторую лемнискатную константу B = π /(2 ϖ ) ≈ 0,5990701173 [11] [12] [13] [14]
Иногда величины 2 ϖ или A называют константой лемнискаты . [15] [16]
постоянная Гаусса G {\displaystyle G} Карла Фридриха Гаусса , который вычислил его через среднее арифметико-геометрическое как 1 M ( 1 , 2 ) {\displaystyle {\tfrac {1}{M\left(1,{\sqrt {2}}\right)}}} [6] M ( 1 , 2 ) = π ϖ {\displaystyle M\left(1,{\sqrt {2}}\right)={\tfrac {\pi }{\varpi }}} ϖ {\displaystyle \varpi } [а]
Лемнискатная константа ϖ {\displaystyle \varpi } A {\displaystyle A} трансцендентными в Теодором Шнайдером 1937 году, а вторая константа лемнискаты B {\displaystyle B} G {\displaystyle G} [11] [17] [б] Григорий Чудновский доказал, что множество { π , ϖ } {\displaystyle \{\pi ,\varpi \}} алгебраически над Q {\displaystyle \mathbb {Q} } A {\displaystyle A} B {\displaystyle B} [18] [19] { π , M ( 1 , 1 2 ) , M ′ ( 1 , 1 2 ) } {\displaystyle \left\{\pi ,M\left(1,{\tfrac {1}{\sqrt {2}}}\right),M'\left(1,{\tfrac {1}{\sqrt {2}}}\right)\right\}} производную по второй переменной) не является алгебраически независимым над Q {\displaystyle \mathbb {Q} } [20]
π = 2 2 M 3 ( 1 , 1 2 ) M ′ ( 1 , 1 2 ) = 1 G 3 M ′ ( 1 , 1 2 ) . {\displaystyle \pi =2{\sqrt {2}}{\frac {M^{3}\left(1,{\frac {1}{\sqrt {2}}}\right)}{M'\left(1,{\frac {1}{\sqrt {2}}}\right)}}={\frac {1}{G^{3}M'\left(1,{\frac {1}{\sqrt {2}}}\right)}}.}
Обычно, ϖ {\displaystyle \varpi } [21] [22]
ϖ = 2 ∫ 0 1 d t 1 − t 4 = 2 ∫ 0 ∞ d t 1 + t 4 = ∫ 0 1 d t t − t 3 = ∫ 1 ∞ d t t 3 − t = 4 ∫ 0 ∞ ( 1 + t 4 4 − t ) d t = 2 2 ∫ 0 1 1 − t 4 4 d t = 3 ∫ 0 1 1 − t 4 d t = 2 K ( i ) = 1 2 B ( 1 4 , 1 2 ) = Γ ( 1 4 ) 2 2 2 π = 2 − 2 4 ζ ( 3 4 ) 2 ζ ( 1 4 ) 2 = 2.62205 75542 92119 81046 48395 89891 11941 … , {\displaystyle {\begin{aligned}\varpi &=2\int _{0}^{1}{\frac {\mathrm {d} t}{\sqrt {1-t^{4}}}}={\sqrt {2}}\int _{0}^{\infty }{\frac {\mathrm {d} t}{\sqrt {1+t^{4}}}}=\int _{0}^{1}{\frac {\mathrm {d} t}{\sqrt {t-t^{3}}}}=\int _{1}^{\infty }{\frac {\mathrm {d} t}{\sqrt {t^{3}-t}}}\\[6mu]&=4\int _{0}^{\infty }\left({\sqrt[{4}]{1+t^{4}}}-t\right)\,\mathrm {d} t=2{\sqrt {2}}\int _{0}^{1}{\sqrt[{4}]{1-t^{4}}}\mathop {\mathrm {d} t} =3\int _{0}^{1}{\sqrt {1-t^{4}}}\,\mathrm {d} t\\[2mu]&=2K(i)={\tfrac {1}{2}}\mathrm {B} \left({\tfrac {1}{4}},{\tfrac {1}{2}}\right)={\frac {\Gamma \left({\frac {1}{4}}\right)^{2}}{2{\sqrt {2\pi }}}}={\frac {2-{\sqrt {2}}}{4}}{\frac {\zeta \left({\frac {3}{4}}\right)^{2}}{\zeta \left({\frac {1}{4}}\right)^{2}}}\\[5mu]&=2.62205\;75542\;92119\;81046\;48395\;89891\;11941\ldots ,\end{aligned}}}
где К — полный эллиптический интеграл первого рода с модулем к , В — бета-функция , Г — гамма-функция и z — дзета-функция Римана .
Константу лемнискаты также можно вычислить как среднее арифметико-геометрическое. M {\displaystyle M}
ϖ = π M ( 1 , 2 ) . {\displaystyle \varpi ={\frac {\pi }{M\left(1,{\sqrt {2}}\right)}}.}
Более того,
e β ′ ( 0 ) = ϖ π {\displaystyle e^{\beta '(0)}={\frac {\varpi }{\sqrt {\pi }}}}
что аналогично
e ζ ′ ( 0 ) = 1 2 π {\displaystyle e^{\zeta '(0)}={\frac {1}{\sqrt {2\pi }}}}
где β {\displaystyle \beta } бета-функция Дирихле и ζ {\displaystyle \zeta } дзета-функция Римана . [23]
Константа Гаусса обычно определяется как обратная величина среднего арифметико-геометрического числа 1 и квадратного корня из 2 после его вычисления M ( 1 , 2 ) {\displaystyle M\left(1,{\sqrt {2}}\right)}
G = 1 M ( 1 , 2 ) {\displaystyle G={\frac {1}{M(1,{\sqrt {2}})}}}
Постоянная Гаусса равна
G = 1 2 π B ( 1 4 , 1 2 ) {\displaystyle G={\frac {1}{2\pi }}\mathrm {B} \left({\tfrac {1}{4}},{\tfrac {1}{2}}\right)}
где В обозначает бета-функцию . Формула для G в терминах тэта-функций Якоби имеет вид
G = ϑ 01 2 ( e − π ) {\displaystyle G=\vartheta _{01}^{2}\left(e^{-\pi }\right)}
Константа Гаусса может быть вычислена из гамма-функции в аргументе 1 / 4
G = Γ ( 1 4 ) 2 2 2 π 3 {\displaystyle G={\frac {\Gamma \left({\tfrac {1}{4}}\right){}^{2}}{2{\sqrt {2\pi ^{3}}}}}}
Константы лемнискаты Джона Тодда можно выразить через бета-функцию B:
A = 1 2 π G = 1 2 ϖ = 1 4 B ( 1 4 , 1 2 ) , B = 1 2 G = 1 4 B ( 1 2 , 3 4 ) . {\displaystyle {\begin{aligned}A&={\tfrac {1}{2}}\pi G={\tfrac {1}{2}}\varpi ={\tfrac {1}{4}}\mathrm {B} \left({\tfrac {1}{4}},{\tfrac {1}{2}}\right),\\[3mu]B&={\frac {1}{2G}}={\tfrac {1}{4}}\mathrm {B} \left({\tfrac {1}{2}},{\tfrac {3}{4}}\right).\end{aligned}}}
Формулу Вьета для числа π можно записать так:
2 π = 1 2 ⋅ 1 2 + 1 2 1 2 ⋅ 1 2 + 1 2 1 2 + 1 2 1 2 ⋯ {\displaystyle {\frac {2}{\pi }}={\sqrt {\frac {1}{2}}}\cdot {\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\sqrt {\frac {1}{2}}}}}\cdot {\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\sqrt {\frac {1}{2}}}}}}}\cdots }
Аналогичная формула для ϖ : [25]
2 ϖ = 1 2 ⋅ 1 2 + 1 2 1 2 ⋅ 1 2 + 1 2 1 2 + 1 2 1 2 ⋯ {\displaystyle {\frac {2}{\varpi }}={\sqrt {\frac {1}{2}}}\cdot {\sqrt {{\frac {1}{2}}+{\frac {\frac {1}{2}}{\sqrt {\frac {1}{2}}}}}}\cdot {\sqrt {{\frac {1}{2}}+{\frac {\frac {1}{2}}{\sqrt {{\frac {1}{2}}+{\frac {\frac {1}{2}}{\sqrt {\frac {1}{2}}}}}}}}}\cdots }
Произведение Уоллиса для π :
π 2 = ∏ n = 1 ∞ ( 1 + 1 n ) ( − 1 ) n + 1 = ∏ n = 1 ∞ ( 2 n 2 n − 1 ⋅ 2 n 2 n + 1 ) = ( 2 1 ⋅ 2 3 ) ( 4 3 ⋅ 4 5 ) ( 6 5 ⋅ 6 7 ) ⋯ {\displaystyle {\frac {\pi }{2}}=\prod _{n=1}^{\infty }\left(1+{\frac {1}{n}}\right)^{(-1)^{n+1}}=\prod _{n=1}^{\infty }\left({\frac {2n}{2n-1}}\cdot {\frac {2n}{2n+1}}\right)=\left({\frac {2}{1}}\cdot {\frac {2}{3}}\right)\left({\frac {4}{3}}\cdot {\frac {4}{5}}\right)\left({\frac {6}{5}}\cdot {\frac {6}{7}}\right)\cdots }
Аналогичная формула для ϖ : [26]
ϖ 2 = ∏ n = 1 ∞ ( 1 + 1 2 n ) ( − 1 ) n + 1 = ∏ n = 1 ∞ ( 4 n − 1 4 n − 2 ⋅ 4 n 4 n + 1 ) = ( 3 2 ⋅ 4 5 ) ( 7 6 ⋅ 8 9 ) ( 11 10 ⋅ 12 13 ) ⋯ {\displaystyle {\frac {\varpi }{2}}=\prod _{n=1}^{\infty }\left(1+{\frac {1}{2n}}\right)^{(-1)^{n+1}}=\prod _{n=1}^{\infty }\left({\frac {4n-1}{4n-2}}\cdot {\frac {4n}{4n+1}}\right)=\left({\frac {3}{2}}\cdot {\frac {4}{5}}\right)\left({\frac {7}{6}}\cdot {\frac {8}{9}}\right)\left({\frac {11}{10}}\cdot {\frac {12}{13}}\right)\cdots }
Связанный результат для постоянной Гаусса ( G = ϖ π {\displaystyle G={\tfrac {\varpi }{\pi }}} [27]
G = ∏ n = 1 ∞ ( 4 n − 1 4 n ⋅ 4 n + 2 4 n + 1 ) = ( 3 4 ⋅ 6 5 ) ( 7 8 ⋅ 10 9 ) ( 11 12 ⋅ 14 13 ) ⋯ {\displaystyle G=\prod _{n=1}^{\infty }\left({\frac {4n-1}{4n}}\cdot {\frac {4n+2}{4n+1}}\right)=\left({\frac {3}{4}}\cdot {\frac {6}{5}}\right)\left({\frac {7}{8}}\cdot {\frac {10}{9}}\right)\left({\frac {11}{12}}\cdot {\frac {14}{13}}\right)\cdots }
Бесконечная серия констант Гаусса, открытая Гауссом: [28]
G = ∑ n = 0 ∞ ( − 1 ) n ∏ k = 1 n ( 2 k − 1 ) 2 ( 2 k ) 2 = 1 − 1 2 2 2 + 1 2 ⋅ 3 2 2 2 ⋅ 4 2 − 1 2 ⋅ 3 2 ⋅ 5 2 2 2 ⋅ 4 2 ⋅ 6 2 + ⋯ {\displaystyle G=\sum _{n=0}^{\infty }(-1)^{n}\prod _{k=1}^{n}{\frac {(2k-1)^{2}}{(2k)^{2}}}=1-{\frac {1^{2}}{2^{2}}}+{\frac {1^{2}\cdot 3^{2}}{2^{2}\cdot 4^{2}}}-{\frac {1^{2}\cdot 3^{2}\cdot 5^{2}}{2^{2}\cdot 4^{2}\cdot 6^{2}}}+\cdots }
Формула Мачина для π : 1 4 π = 4 arctan 1 5 − arctan 1 239 , {\textstyle {\tfrac {1}{4}}\pi =4\arctan {\tfrac {1}{5}}-\arctan {\tfrac {1}{239}},} π можно получить, используя тождества суммы тригонометрических углов, например, формулу Эйлера 1 4 π = arctan 1 2 + arctan 1 3 {\textstyle {\tfrac {1}{4}}\pi =\arctan {\tfrac {1}{2}}+\arctan {\tfrac {1}{3}}} ϖ , включая следующие, найденные Гауссом: 1 2 ϖ = 2 arcsl 1 2 + arcsl 7 23 {\displaystyle {\tfrac {1}{2}}\varpi =2\operatorname {arcsl} {\tfrac {1}{2}}+\operatorname {arcsl} {\tfrac {7}{23}}} arcsl {\displaystyle \operatorname {arcsl} } лемниската арксинус . [29]
Константу лемнискаты можно быстро вычислить по ряду [30] [31]
ϖ = 1 2 π ( ∑ n ∈ Z e − π n 2 ) 2 = 2 4 π e − π 12 ( ∑ n ∈ Z ( − 1 ) n e − π p n ) 2 {\displaystyle \varpi ={\frac {1}{\sqrt {2}}}\pi \left(\sum _{n\in \mathbb {Z} }e^{-\pi n^{2}}\right)^{2}={\sqrt[{4}]{2}}\pi e^{-{\frac {\pi }{12}}}\left(\sum _{n\in \mathbb {Z} }(-1)^{n}e^{-\pi p_{n}}\right)^{2}} где p n = 3 n 2 − n 2 {\displaystyle p_{n}={\tfrac {3n^{2}-n}{2}}} обобщенные пятиугольные числа ).
В духе, аналогичном Базельской проблеме ,
∑ z ∈ Z [ i ] ∖ { 0 } 1 z 4 = G 4 ( i ) = ϖ 4 15 {\displaystyle \sum _{z\in \mathbb {Z} [i]\setminus \{0\}}{\frac {1}{z^{4}}}=G_{4}(i)={\frac {\varpi ^{4}}{15}}} где Z [ i ] {\displaystyle \mathbb {Z} [i]} гауссовскими целыми числами и G 4 {\displaystyle G_{4}} ряд Эйзенштейна веса 4 ( см. в разделе «Эллиптические функции Лемнискаты § Числа Гурвица »). более общий результат [32]
Соответствующий результат
∑ n = 1 ∞ σ 3 ( n ) e − 2 π n = ϖ 4 80 π 4 − 1 240 {\displaystyle \sum _{n=1}^{\infty }\sigma _{3}(n)e^{-2\pi n}={\frac {\varpi ^{4}}{80\pi ^{4}}}-{\frac {1}{240}}} где σ 3 {\displaystyle \sigma _{3}} функцию суммы положительных делителей . [33]
В 1842 году Мальмстен нашел
∑ n = 1 ∞ ( − 1 ) n + 1 log ( 2 n + 1 ) 2 n + 1 = π 4 ( γ + 2 log π ϖ 2 ) {\displaystyle \sum _{n=1}^{\infty }(-1)^{n+1}{\frac {\log(2n+1)}{2n+1}}={\frac {\pi }{4}}\left(\gamma +2\log {\frac {\pi }{\varpi {\sqrt {2}}}}\right)} где γ {\displaystyle \gamma } постоянная Эйлера .
Константа Гаусса определяется быстро сходящимся рядом
G = 32 4 e − π 3 ( ∑ n = − ∞ ∞ ( − 1 ) n e − 2 n π ( 3 n + 1 ) ) 2 . {\displaystyle G={\sqrt[{4}]{32}}e^{-{\frac {\pi }{3}}}\left(\sum _{n=-\infty }^{\infty }(-1)^{n}e^{-2n\pi (3n+1)}\right)^{2}.}
Константа также определяется бесконечным произведением
G = ∏ m = 1 ∞ tanh 2 ( π m 2 ) . {\displaystyle G=\prod _{m=1}^{\infty }\tanh ^{2}\left({\frac {\pi m}{2}}\right).} Цепные дроби [ править ] (Обобщенная) цепная дробь для π равна
π 2 = 1 + 1 1 + 1 ⋅ 2 1 + 2 ⋅ 3 1 + 3 ⋅ 4 1 + ⋱ {\displaystyle {\frac {\pi }{2}}=1+{\cfrac {1}{1+{\cfrac {1\cdot 2}{1+{\cfrac {2\cdot 3}{1+{\cfrac {3\cdot 4}{1+\ddots }}}}}}}}} Аналогичная формула для
ϖ :
[12] ϖ 2 = 1 + 1 2 + 2 ⋅ 3 2 + 4 ⋅ 5 2 + 6 ⋅ 7 2 + ⋱ {\displaystyle {\frac {\varpi }{2}}=1+{\cfrac {1}{2+{\cfrac {2\cdot 3}{2+{\cfrac {4\cdot 5}{2+{\cfrac {6\cdot 7}{2+\ddots }}}}}}}}}
Определите Брункера непрерывную дробь [34]
b ( s ) = s + 1 2 2 s + 3 2 2 s + 5 2 2 s + ⋱ , s > 0. {\displaystyle b(s)=s+{\cfrac {1^{2}}{2s+{\cfrac {3^{2}}{2s+{\cfrac {5^{2}}{2s+\ddots }}}}}},\quad s>0.} Позволять
n ≥ 0 {\displaystyle n\geq 0} кроме первого равенства, где
n ≥ 1 {\displaystyle n\geq 1} . Затем
[35] [36] b ( 4 n ) = ( 4 n + 1 ) ∏ k = 1 n ( 4 k − 1 ) 2 ( 4 k − 3 ) ( 4 k + 1 ) π ϖ 2 b ( 4 n + 1 ) = ( 2 n + 1 ) ∏ k = 1 n ( 2 k ) 2 ( 2 k − 1 ) ( 2 k + 1 ) 4 π b ( 4 n + 2 ) = ( 4 n + 1 ) ∏ k = 1 n ( 4 k − 3 ) ( 4 k + 1 ) ( 4 k − 1 ) 2 ϖ 2 π b ( 4 n + 3 ) = ( 2 n + 1 ) ∏ k = 1 n ( 2 k − 1 ) ( 2 k + 1 ) ( 2 k ) 2 π . {\displaystyle {\begin{aligned}b(4n)&=(4n+1)\prod _{k=1}^{n}{\frac {(4k-1)^{2}}{(4k-3)(4k+1)}}{\frac {\pi }{\varpi ^{2}}}\\b(4n+1)&=(2n+1)\prod _{k=1}^{n}{\frac {(2k)^{2}}{(2k-1)(2k+1)}}{\frac {4}{\pi }}\\b(4n+2)&=(4n+1)\prod _{k=1}^{n}{\frac {(4k-3)(4k+1)}{(4k-1)^{2}}}{\frac {\varpi ^{2}}{\pi }}\\b(4n+3)&=(2n+1)\prod _{k=1}^{n}{\frac {(2k-1)(2k+1)}{(2k)^{2}}}\,\pi .\end{aligned}}} Например,
b ( 1 ) = 4 π b ( 2 ) = ϖ 2 π b ( 3 ) = π b ( 4 ) = 9 π ϖ 2 . {\displaystyle {\begin{aligned}b(1)&={\frac {4}{\pi }}\\b(2)&={\frac {\varpi ^{2}}{\pi }}\\b(3)&=\pi \\b(4)&={\frac {9\pi }{\varpi ^{2}}}.\end{aligned}}}
ϖ = [ 2 , 1 , 1 , 1 , 1 , 1 , 4 , 1 , 2 , … ] 2 ϖ = [ 5 , 4 , 10 , 2 , 1 , 2 , 3 , 29 , … ] ϖ 2 = [ 1 , 3 , 4 , 1 , 1 , 1 , 5 , 2 , … ] G = [ 0 , 1 , 5 , 21 , 3 , 4 , 14 , … ] {\displaystyle {\begin{aligned}\varpi &=[2,1,1,1,1,1,4,1,2,\ldots ]\\2\varpi &=[5,4,10,2,1,2,3,29,\ldots ]\\{\frac {\varpi }{2}}&=[1,3,4,1,1,1,5,2,\ldots ]\\G&=[0,1,5,21,3,4,14,\ldots ]\end{aligned}}}
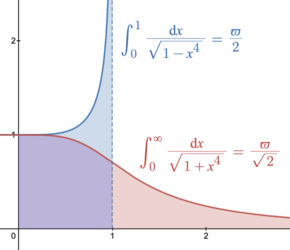
Геометрическое представление ϖ / 2 {\displaystyle \varpi /2} ϖ / 2 {\displaystyle \varpi /{\sqrt {2}}} ϖ относится к площади под кривой x 4 + y 4 = 1 {\displaystyle x^{4}+y^{4}=1} π n := B ( 1 n , 1 n ) {\displaystyle \pi _{n}\mathrel {:=} \mathrm {B} \left({\tfrac {1}{n}},{\tfrac {1}{n}}\right)} x n + y n = 1 {\displaystyle x^{n}+y^{n}=1}
2 ∫ 0 1 1 − x n n d x = 1 n π n . {\displaystyle 2\int _{0}^{1}{\sqrt[{n}]{1-x^{n}}}\mathop {\mathrm {d} x} ={\tfrac {1}{n}}\pi _{n}.} В квартическом случае
1 4 π 4 = 1 2 ϖ . {\displaystyle {\tfrac {1}{4}}\pi _{4}={\tfrac {1}{\sqrt {2}}}\varpi .}
В 1842 году Мальмстен обнаружил, что [39]
∫ 0 1 log ( − log x ) 1 + x 2 d x = π 2 log π ϖ 2 . {\displaystyle \int _{0}^{1}{\frac {\log(-\log x)}{1+x^{2}}}\,dx={\frac {\pi }{2}}\log {\frac {\pi }{\varpi {\sqrt {2}}}}.}
Более того,
∫ 0 ∞ tanh x x e − x d x = log ϖ 2 π {\displaystyle \int _{0}^{\infty }{\frac {\tanh x}{x}}e^{-x}\,dx=\log {\frac {\varpi ^{2}}{\pi }}}
и [40]
∫ 0 ∞ e − x 4 d x = 2 ϖ 2 π 4 , analogous to ∫ 0 ∞ e − x 2 d x = π 2 , {\displaystyle \int _{0}^{\infty }e^{-x^{4}}\,dx={\frac {\sqrt {2\varpi {\sqrt {2\pi }}}}{4}},\quad {\text{analogous to}}\,\int _{0}^{\infty }e^{-x^{2}}\,dx={\frac {\sqrt {\pi }}{2}},} разновидность
интеграла Гаусса .
Константа Гаусса появляется при вычислении интегралов
1 G = ∫ 0 π 2 sin ( x ) d x = ∫ 0 π 2 cos ( x ) d x {\displaystyle {\frac {1}{G}}=\int _{0}^{\frac {\pi }{2}}{\sqrt {\sin(x)}}\,dx=\int _{0}^{\frac {\pi }{2}}{\sqrt {\cos(x)}}\,dx}
G = ∫ 0 ∞ d x cosh ( π x ) {\displaystyle G=\int _{0}^{\infty }{\frac {dx}{\sqrt {\cosh(\pi x)}}}}
Первая и вторая константы лемнискаты определяются интегралами: [11]
A = ∫ 0 1 d x 1 − x 4 {\displaystyle A=\int _{0}^{1}{\frac {dx}{\sqrt {1-x^{4}}}}}
B = ∫ 0 1 x 2 d x 1 − x 4 {\displaystyle B=\int _{0}^{1}{\frac {x^{2}\,dx}{\sqrt {1-x^{4}}}}}
Длина окружности эллипса [ править ] Постоянная Гаусса удовлетворяет уравнению
1 G = 2 ∫ 0 1 x 2 d x 1 − x 4 {\displaystyle {\frac {1}{G}}=2\int _{0}^{1}{\frac {x^{2}\,dx}{\sqrt {1-x^{4}}}}}
Эйлер открыл в 1738 году, что для прямоугольной эластики (первая и вторая константы лемнискаты) [42]
arc length ⋅ height = A ⋅ B = ∫ 0 1 d x 1 − x 4 ⋅ ∫ 0 1 x 2 d x 1 − x 4 = ϖ 2 ⋅ π 2 ϖ = π 4 {\displaystyle {\textrm {arc}}\ {\textrm {length}}\cdot {\textrm {height}}=A\cdot B=\int _{0}^{1}{\frac {\mathrm {d} x}{\sqrt {1-x^{4}}}}\cdot \int _{0}^{1}{\frac {x^{2}\mathop {\mathrm {d} x} }{\sqrt {1-x^{4}}}}={\frac {\varpi }{2}}\cdot {\frac {\pi }{2\varpi }}={\frac {\pi }{4}}}
Теперь учитывая окружность C {\displaystyle C} 2 {\displaystyle {\sqrt {2}}} 1 {\displaystyle 1} 2 x 2 + 4 y 2 = 1 {\displaystyle 2x^{2}+4y^{2}=1}
C 2 = ∫ 0 1 d x 1 − x 4 + ∫ 0 1 x 2 d x 1 − x 4 {\displaystyle {\frac {C}{2}}=\int _{0}^{1}{\frac {dx}{\sqrt {1-x^{4}}}}+\int _{0}^{1}{\frac {x^{2}\,dx}{\sqrt {1-x^{4}}}}}
Следовательно, полная окружность равна
C = 1 G + G π ≈ 3.820197789 … {\displaystyle C={\frac {1}{G}}+G\pi \approx 3.820197789\ldots }
Это также длина дуги синусоиды на половине периода: [44]
C = ∫ 0 π 1 + cos 2 ( x ) d x {\displaystyle C=\int _{0}^{\pi }{\sqrt {1+\cos ^{2}(x)}}\,dx}
Другие ограничения [ править ] Аналогично
2 π = lim n → ∞ | ( 2 n ) ! B 2 n | 1 2 n {\displaystyle 2\pi =\lim _{n\to \infty }\left|{\frac {(2n)!}{\mathrm {B} _{2n}}}\right|^{\frac {1}{2n}}} где
B n {\displaystyle \mathrm {B} _{n}} являются
числами Бернулли , мы имеем
2 ϖ = lim n → ∞ ( ( 4 n ) ! H 4 n ) 1 4 n {\displaystyle 2\varpi =\lim _{n\to \infty }\left({\frac {(4n)!}{\mathrm {H} _{4n}}}\right)^{\frac {1}{4n}}} где
H n {\displaystyle \mathrm {H} _{n}} являются
числами Гурвица .
Примечания [ править ] ^ хотя ни одно из этих доказательств не было строгим с современной точки зрения. ^ В частности, он доказал, что бета-функция B ( a , b ) {\displaystyle \mathrm {B} (a,b)} a , b ∈ Q ∖ Z {\displaystyle a,b\in \mathbb {Q} \setminus \mathbb {Z} } a + b ∉ Z 0 − {\displaystyle a+b\notin \mathbb {Z} _{0}^{-}} ϖ {\displaystyle \varpi } ϖ = 1 2 B ( 1 4 , 1 2 ) {\displaystyle \varpi ={\tfrac {1}{2}}\mathrm {B} \left({\tfrac {1}{4}},{\tfrac {1}{2}}\right)} B и G из B ( 1 2 , 3 4 ) . {\displaystyle \mathrm {B} \left({\tfrac {1}{2}},{\tfrac {3}{4}}\right).} ^ Гаусс, CF (1866). Сочинения (Том III) ^ Эймар, Пьер; Лафон, Жан-Пьер (2004). Число Пи . Американское математическое общество. ISBN 0-8218-3246-8 ^ Боттаццини, Умберто ; Грей, Джереми (2013). Скрытая гармония – геометрические фантазии: возникновение теории комплексных функций . Спрингер. дои : 10.1007/978-1-4614-5725-1 . ISBN 978-1-4614-5724-4 ^ Аракава, Цунео; Ибукияма, Томоёси; Бернулли и дзета-функции . Числа 978-4-431-54918-5 ^ Jump up to: Перейти обратно: а б Финч, Стивен Р. (18 августа 2003 г.). Математические константы ИСБН 978-0-521-81805-6 ^ Кобаяши, Хироюки; Такеучи, Шинго (2019), «Применение обобщенных тригонометрических функций с двумя параметрами», Communications on Pure & Applied Analysis , 18 (3): 1509–1521, arXiv : 1903.07407 doi : 10.3934/cpaa.2019072 , S2CID 102487670 ^ Асаи, Тецуя (2007), Эллиптические суммы Гаусса и L-значения Хекке при s=1 , arXiv : 0707,3711 ^ "А062539 - Оайс" . ^ "A014549 - Оайс" . ^ Jump up to: Перейти обратно: а б с Тодд, Джон (январь 1975 г.). «Лемнискатные константы» . Коммуникации АКМ 18 (1): 14–19. дои : 10.1145/360569.360580 S2CID 85873 . ^ Jump up to: Перейти обратно: а б "A085565 - Оайс" . ^ «А076390 - Оайс» . ^ Карлсон, Британская Колумбия (2010), «Эллиптические интегралы» , Олвер, Фрэнк У.Дж .; Лозье, Дэниел М.; Буасверт, Рональд Ф.; Кларк, Чарльз В. (ред.), Справочник NIST по математическим функциям ISBN 978-0-521-19225-5 МР 2723248 ^ "A064853 - Оайс" . ^ «Лемниската Константа» . ^ Шнайдер, Теодор (1941). «К теории абелевых функций и интегралов» . Журнал чистой и прикладной математики . 183 (19): 110–128. дои : 10.1515/crll.1941.183.110 . S2CID 118624331 . ^ Г. В. Чудновский: Алгебраическая независимость констант, связанных с функциями анализа , Извещения AMS 22, 1975, с. А-486 ^ Г. В. Чудновский: Вклад в теорию трансцендентных чисел , Американское математическое общество, 1984, с. 6 ^ Борвейн, Джонатан М.; Борвейн, Питер Б. (1987). Пи и AGM: исследование аналитической теории чисел и сложности вычислений (первое изд.). Уайли-Интерсайенс. ISBN 0-471-83138-7 ^ Финч, Стивен Р. (18 августа 2003 г.). Математические константы ISBN 978-0-521-81805-6 ^ Шаппахер, Норберт (1997). «Некоторые вехи лемнискатомии» (PDF) . В Сертёзе, С. (ред.). Алгебраическая геометрия (Материалы летней школы Билкент, 7–19 августа 1995 г., Анкара, Турция). Марсель Деккер. стр. 257–290. ^ «А113847 — Оайс» . ^ Левин (2006) ^ Хайд (2014) доказывает справедливость более общей формулы Уоллиса для кривых клевера; здесь для ясности частный случай лемнискаты немного трансформируется. ^ Хайд, Тревор (2014). «Продукт Уоллиса на клевере» (PDF) . Американский математический ежемесячник . 121 (3): 237–243. doi : 10.4169/amer.math.monthly.121.03.237 . S2CID 34819500 . ^ Боттаццини, Умберто ; Грей, Джереми (2013). Скрытая гармония – геометрические фантазии: возникновение теории комплексных функций . Спрингер. дои : 10.1007/978-1-4614-5725-1 . ISBN 978-1-4614-5724-4 ^ Тодд (1975) ^ Кокс 1984 , с. 307, экв. 2.21 для первого равенства. Второе равенство можно доказать, используя теорему о пятиугольных числах . ^ Берндт, Брюс К. (1998). Записные книжки Рамануджана . Часть V. Спрингер. ISBN 978-1-4612-7221-2 ^ Эймар, Пьер; Лафон, Жан-Пьер (2004). Число Пи . Американское математическое общество. ISBN 0-8218-3246-8 ^ Гарретт, Пол. «Эллиптические модульные формы первого уровня» (PDF) . Университет Миннесоты . ^ Хрущев, Сергей (2008). Ортогональные многочлены и цепные дроби (Первое изд.). Издательство Кембриджского университета. ISBN 978-0-521-85419-1 4 [ Γ ( 3 + s / 4 ) / Γ ( 1 + s / 4 ) ] 2 {\displaystyle 4[\Gamma (3+s/4)/\Gamma (1+s/4)]^{2}} 4 [ Γ ( ( 3 + s ) / 4 ) / Γ ( ( 1 + s ) / 4 ) ] 2 {\displaystyle 4[\Gamma ((3+s)/4)/\Gamma ((1+s)/4)]^{2}} ^ Хрущев, Сергей (2008). Ортогональные многочлены и цепные дроби (Первое изд.). Издательство Кембриджского университета. ISBN 978-0-521-85419-1 ^ Перрон, Оскар (1957). Учение о цепных дробях: Том II (на немецком языке) (Третье изд.). Б. Г. Тойбнер. ^ «А062540-ОЭИС» . oeis.org . Проверено 14 сентября 2022 г. ^ «А053002-ОЭИС» . oeis.org . ^ Благоушин, Ярослав В. (2014). «Повторное открытие интегралов Мальмстена, их оценка методами контурного интегрирования и некоторые связанные с этим результаты» . Журнал Рамануджана . 35 (1): 21–110. дои : 10.1007/s11139-013-9528-5 . S2CID 120943474 . ^ "A068467 - Оэйс" . ^ Левиен (2008) ^ Адлай, Семен (2012). «Красноречивая формула периметра эллипса» (PDF) . Американское математическое общество . п. 1097. Можно также заметить, что длина «синусоидальной» кривой за половину периода, т. е. длина графика функции sin(t) от точки, где t = 0, до точки, где t = π, является 2 l ( 1 / 2 ) = L + M {\displaystyle {\sqrt {2}}l(1/{\sqrt {2}})=L+M} M = 1 / G = π / ϖ {\displaystyle M=1/G=\pi /\varpi } L = π / M = G π = ϖ {\displaystyle L=\pi /M=G\pi =\varpi } Внешние ссылки [ править ]












![{\displaystyle {\begin{aligned}\varpi &=2\int _{0}^{1}{\frac {\mathrm {d} t}{\sqrt {1-t^{4}}}}= {\sqrt {2}}\int _{0}^{\infty }{\frac {\mathrm {d} t}{\sqrt {1+t^{4}}}}=\int _{0} ^{1}{\frac {\mathrm {d} t}{\sqrt {tt^{3}}}}=\int _{1}^{\infty }{\frac {\mathrm {d} t} {\sqrt {t^{3}-t}}}\\[6mu]&=4\int _{0}^{\infty }\left({\sqrt[{4}]{1+t^{ 4}}}-t\right)\,\mathrm {d} t=2{\sqrt {2}}\int _{0}^{1}{\sqrt[{4}]{1-t^{ 4}}}\mathop {\mathrm {d} t} =3\int _{0}^{1}{\sqrt {1-t^{4}}}\,\mathrm {d} t\\[ 2mu]&=2K(i)={\tfrac {1}{2}}\mathrm {B} \left({\tfrac {1}{4}},{\tfrac {1}{2}}\right )={\frac {\Gamma \left({\frac {1}{4}}\right)^{2}}{2{\sqrt {2\pi }}}}={\frac {2-{ \sqrt {2}}}{4}}{\frac {\zeta \left({\frac {3}{4}}\right)^{2}}{\zeta \left({\frac {1} {4}}\right)^{2}}}\\[5mu]&=2.62205\;75542\;92119\;81046\;48395\;89891\;11941\ldots ,\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9bf7c7233bf4b6269942dec05ba1a3ac217f4cbf)











![{\displaystyle {\begin{aligned}A&={\tfrac {1}{2}}\pi G={\tfrac {1}{2}}\varpi ={\tfrac {1}{4}}\mathrm {B} \left({\tfrac {1}{4}},{\tfrac {1}{2}}\right),\\[3mu]B&={\frac {1}{2G}}={ \tfrac {1}{4}}\mathrm {B} \left({\tfrac {1}{2}},{\tfrac {3}{4}}\right).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/06ccbacee3aab03e1e6683adc5d34b7d94f17a9e)











![{\displaystyle \varpi ={\frac {1}{\sqrt {2}}}\pi \left(\sum _{n\in \mathbb {Z} }e^{-\pi n^{2}} \right)^{2}={\sqrt[{4}]{2}}\pi e^{-{\frac {\pi }{12}}}\left(\sum _{n\in \mathbb {Z} }(-1)^{n}e^{-\pi p_{n}}\right)^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ece0fb5f540bbe746d500f986f76b033b181d1ae)

![{\displaystyle \sum _{z\in \mathbb {Z} [i]\setminus \{0\}}{\frac {1}{z^{4}}}=G_{4}(i)={ \frac {\varpi ^{4}}{15}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e2c020975bd00f51d682f805befa01df23988448)
![{\displaystyle \mathbb {Z} [я]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ffa94e9e2e6d9e5e5373d5fafb954b902743fde)





![{\displaystyle G={\sqrt[{4}]{32}}e^{- {\frac {\pi }{3}}}\left(\sum _{n=-\infty }^{\infty }(-1)^{n}e^{-2n\pi (3n+1)}\right)^{2}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa19577531f9b3da22813ac592a0c28c2145114e)








![{\displaystyle {\begin{aligned}\varpi &=[2,1,1,1,1,1,4,1,2,\ldots ]\\2\varpi &=[5,4,10,2 ,1,2,3,29,\ldots ]\\{\frac {\varpi }{2}}&=[1,3,4,1,1,1,5,2,\ldots ]\\G& =[0,1,5,21,3,4,14,\ldots ]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3a623cc8ce04d3caf2aa7f0edfc8ac7ca8a684e4)





![{\displaystyle 2\int _{0}^{1}{\sqrt[{n}]{1-x^{n}}}\mathop {\mathrm {d} x} ={\tfrac {1}{ n}}\pi _{n}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0de1a90168b1c55ec9447e41dc5b318d2e06bfef)


























![{\displaystyle 4[\Гамма (3+s/4)/\Гамма (1+s/4)]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7dbbf0163687acf39aec82572e89e1cfc9814f41)
![{\displaystyle 4[\Гамма ((3+s)/4)/\Гамма ((1+s)/4)]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9e3daa83f9526cd20ebe1bddfefa93546ba20d1d)



