Математическая индукция

Не путать с индуктивным рассуждением .

Математическая индукция может быть неформально проиллюстрирована ссылкой на последовательный эффект падения домино .

Математическая индукция – это метод доказательства того, что утверждение $P(n)$ верно для любого натурального числа $n$, то есть бесконечно много случаев $P(0),P(1),P(2),P(3),\dots$ все держится. Для этого сначала доказывается простой случай, а затем показывается, что если мы предположим, что утверждение истинно для данного случая, то и следующий случай также будет истинным. Неформальные метафоры помогают объяснить эту технику, например, падение домино или подъем по лестнице:

Математическая индукция доказывает, что мы можем подняться по лестнице так высоко, как нам хочется, доказывая, что мы можем подняться на нижнюю ступеньку (основание ) и что с каждой ступеньки мы можем подняться на следующую (ступеньку ) .

— Конкретная математика , поля 3 страницы.

Доказательство по индукции состоит из двух случаев. Первый, базовый случай , доказывает утверждение для $n=0$ не предполагая никакого знания других случаев. Второй случай, шаг индукции , доказывает, что если утверждение верно для любого данного случая $n=k$, то оно должно выполняться и для следующего случая $n=k+1$. Эти два шага устанавливают, что утверждение справедливо для любого натурального числа. $n$. Базовый вариант не обязательно начинается с $n=0$, но часто с $n=1$и, возможно, с любым фиксированным натуральным числом $n=N$, устанавливая истинность утверждения для всех натуральных чисел $n\geq N$.

Метод можно расширить для доказательства утверждений о более общих обоснованных структурах, таких как деревья ; это обобщение, известное как структурная индукция , используется в математической логике и информатике . Математическая индукция в этом расширенном смысле тесно связана с рекурсией . Математическая индукция — это правило вывода, используемое в формальных доказательствах , и основа большинства доказательств правильности компьютерных программ.

Несмотря на свое название, математическая индукция фундаментально отличается от индуктивного рассуждения , используемого в философии , в котором исследование многих случаев приводит к вероятному заключению. Математический метод исследует бесконечное множество случаев, чтобы доказать общее утверждение, но делает это с помощью конечной цепочки дедуктивных рассуждений, включающих переменную. $n$, который может принимать бесконечное количество значений. Результатом является строгое доказательство утверждения, а не утверждение его вероятности.

История

В 370 г. до н.э. « Платона » Парменид , возможно, содержал следы раннего примера неявного индуктивного доказательства: однако самое раннее неявное доказательство методом математической индукции было написано аль-Караджи около 1000 года нашей эры, который применил его к арифметическим последовательностям для доказательства биномиальной теоремы и свойств треугольника Паскаля . Хотя оригинальная работа была утеряна, позже на нее ссылался Аль-Самавал аль-Магриби в своем трактате аль-Бахир фил-джабр («Блестящие алгебры») примерно в 1150 году нашей эры.

Кац говорит в своей истории математики

Другая важная идея, предложенная аль-Караджи и продолженная ас-Самауалем и другими, заключалась в индуктивном аргументе для работы с определенными арифметическими последовательностями. Таким образом, аль-Караджи использовал такой аргумент, чтобы доказать результат о суммах целых кубов, уже известный Арьябхате [...] Аль-Караджи, однако, не сформулировал общий результат для произвольного n . Он сформулировал свою теорему для конкретного целого числа 10 [...] Его доказательство, тем не менее, было явно рассчитано на распространение на любое другое целое число. [...] Аргумент Аль-Караджи включает в себя, по сути, два основных компонента современного аргумента по индукции, а именно истинность утверждения для n = 1 (1 = 1 ³ ) и вывод истины для n = k из истины для n = k - 1. Конечно, этот второй компонент не является явным, поскольку в некотором смысле аргумент аль-Караджи является обратным; то есть он начинает с n = 10 и опускается до 1, а не идет вверх. Тем не менее, его аргумент в аль-Фахри является самым ранним из сохранившихся доказательств формулы суммы для целых кубов .

В Индии первые неявные доказательства методом математической индукции появляются в » Бхаскары « циклическом методе .

Однако ни один из этих древних математиков не сформулировал в явном виде гипотезу индукции. Другой подобный случай (вопреки тому, что написал Вакка, как тщательно показал Фройденталь) был метод Франческо Мауролико в его дуэте Arithmeticorum libri (1575 г.), который использовал эту технику, чтобы доказать, что сумма первых n нечетных целых чисел равна n. ² .

Самое раннее строгое использование индукции было у Герсонида (1288–1344). Первая явная формулировка принципа индукции была дана Паскалем в его «Трактате о треугольной арифметике» (1665). Другой француз, Ферма , широко использовал схожий принцип: косвенное доказательство путем бесконечного спуска .

Гипотезу индукции также использовал швейцарец Якоб Бернулли , и с тех пор она стала широко известна. Современная формальная трактовка этого принципа появилась только в XIX веке, благодаря Джорджу Булю . Огастес Де Морган , Чарльз Сандерс Пирс Джузеппе Пеано и Ричард Дедекинд .

Описание

Самая простая и распространенная форма математической индукции предполагает, что утверждение, включающее натуральное число n (то есть целое число n ≥ 0 или 1), справедливо для всех значений n . Доказательство состоит из двух шагов:

1. The базовый случай (или начальный случай ): докажите, что утверждение справедливо для 0 или 1.
2. The шаг индукции (или индуктивный шаг , или случай шага ): докажите, что для каждого n , если утверждение верно для n , то оно справедливо и для n + 1 . Другими словами, предположим, что утверждение справедливо для некоторого произвольного натурального числа n , и докажем, что оно справедливо для n + 1 .

Гипотеза на этапе индукции о том, что утверждение справедливо для определенного n , называется гипотезой индукции или индуктивной гипотезой . Чтобы доказать шаг индукции, принимается гипотеза индукции для n , а затем используется это предположение, чтобы доказать, что утверждение справедливо для n + 1 .

Авторы, которые предпочитают определять натуральные числа начиная с 0, используют это значение в базовом случае; те, кто определяет натуральные числа начиная с 1, используют это значение.

Примеры

Сумма последовательных натуральных чисел

Математической индукцией можно воспользоваться, чтобы доказать следующее утверждение P ( n ) для всех натуральных чисел n .

$$P(n)\!:\ \ 0+1+2+\cdots +n={\frac {n(n+1)}{2}}.$$

Это формула общей формулы суммы натуральных чисел, меньших или равных данному числу; фактически бесконечная последовательность утверждений: $0={\tfrac {(0)(0+1)}{2}}$, $0+1={\tfrac {(1)(1+1)}{2}}$, $0+1+2={\tfrac {(2)(2+1)}{2}}$, и т. д.

Предложение. Для каждого $n\in \mathbb {N}$, $0+1+2+\cdots +n={\tfrac {n(n+1)}{2}}.$

Доказательство. Пусть P ( n ) будет утверждением $0+1+2+\cdots +n={\tfrac {n(n+1)}{2}}.$ Доказательство дадим индукцией по n .

Базовый случай: покажите, что утверждение справедливо для наименьшего натурального числа n = 0 .

P (0) явно верно: $0={\tfrac {0(0+1)}{2}}\,.$

Шаг индукции: покажите, что для любого k ≥ 0 , если P ( k ) выполняется, то P ( k + 1) также выполняется.

Предположим, что по индукционному предположению для конкретного k выполняется единственный случай n = k , что означает, что P ( k ) верно:

$$0+1+\cdots +k={\frac {k(k+1)}{2}}.$$

Отсюда следует, что:

$$(0+1+2+\cdots +k)+(k+1)={\frac {k(k+1)}{2}}+(k+1).$$

Алгебраически правая часть упрощается как:

$${\begin{aligned}{\frac {k(k+1)}{2}}+(k+1)&={\frac {k(k+1)+2(k+1)}{2}}\\&={\frac {(k+1)(k+2)}{2}}\\&={\frac {(k+1)((k+1)+1)}{2}}.\end{aligned}}$$

Приравнивая крайние левую и правую части, получаем, что:

$$0+1+2+\cdots +k+(k+1)={\frac {(k+1)((k+1)+1)}{2}}.$$

То есть утверждение P ( k +1) также верно, устанавливая шаг индукции.

Вывод: поскольку и базовый случай, и шаг индукции оказались верными, с помощью математической индукции утверждение P ( n ) справедливо для любого натурального числа n . КЭД

Тригонометрическое неравенство

Индукция часто используется для доказательства неравенств . В качестве примера мы доказываем, что $\left|\sin nx\right|\leq n\left|\sin x\right|$ для любого действительного числа $x$ и натуральное число $n$.

На первый взгляд может показаться, что это более общая версия, $\left|\sin nx\right|\leq n\left|\sin x\right|$ для любых действительных чисел $n,x$, можно доказать без индукции; но случай ${\textstyle n={\frac {1}{2}},\,x=\pi }$ показывает, что это может быть ложным для нецелых значений $n$. Это предполагает, что мы рассмотрим это утверждение специально для естественных ценностей $n$, а индукция — самый удобный инструмент.

Предложение. Для любого $x\in \mathbb {R}$ и $n\in \mathbb {N}$, $\left|\sin nx\right|\leq n\left|\sin x\right|$.

Доказательство. Исправить произвольное действительное число $x$, и пусть $P(n)$ быть заявлением $\left|\sin nx\right|\leq n\left|\sin x\right|$. Мы вызываем на $n$.

Базовый вариант: расчет $\left|\sin 0x\right|=0\leq 0=0\left|\sin x\right|$ проверяет $P(0)$.

Шаг индукции: показываем импликацию $P(k)\implies P(k+1)$ для любого натурального числа $k$. Предположим предположение индукции: для заданного значения $n=k\geq 0$, единичный случай $P(k)$ это правда. Используя формулу сложения углов и неравенство треугольника , выводим:

$${\begin{aligned}\left|\sin(k+1)x\right|&=\left|\sin kx\cos x+\sin x\cos kx\right|&&{\text{(angle addition)}}\\&\leq \left|\sin kx\cos x\right|+\left|\sin x\,\cos kx\right|&&{\text{(triangle inequality)}}\\&=\left|\sin kx\right|\left|\cos x\right|+\left|\sin x\right|\left|\cos kx\right|\\&\leq \left|\sin kx\right|+\left|\sin x\right|&&(\left|\cos t\right|\leq 1)\\&\leq k\left|\sin x\right|+\left|\sin x\right|&&{\text{(induction hypothesis}})\\&=(k+1)\left|\sin x\right|.\end{aligned}}$$

Неравенство между крайними левыми и правыми величинами показывает, что $P(k+1)$ верно, что завершает этап индукции.

Вывод: предложение $P(n)$ справедливо для всех натуральных чисел $n.$  КЭД

Варианты

На практике доказательства по индукции часто строятся по-разному, в зависимости от точной природы доказываемого свойства.Все варианты индукции представляют собой частные случаи трансфинитной индукции ; см . ниже .

Базовый случай, отличный от 0 или 1

Если кто-то желает доказать утверждение не для всех натуральных чисел, а только для всех чисел n, больших или равных определенному числу b , то доказательство по индукции состоит из следующего:

1. Покажем, что утверждение справедливо, когда n = b .
2. Показывая, что если утверждение справедливо для произвольного числа n ≥ b , то то же самое утверждение справедливо и для n + 1 .

Это можно использовать, например, чтобы показать, что 2 ^н ≥ n + 5 для n ≥ 3 .

Таким образом можно доказать, что некоторое утверждение P ( n ) справедливо для всех n ≥ 1 или даже для всех n ≥ −5 . Эта форма математической индукции на самом деле является частным случаем предыдущей формы, потому что, если доказываемое утверждение представляет собой P ( n ), то доказательство его с помощью этих двух правил эквивалентно доказательству P ( n + b ) для всех натуральных чисел n с индукционный базовый случай 0 .

Пример: формирование долларовых сумм монетами

Предположим, что у нас есть бесконечный запас монет номиналом 4 и 5 долларов. С помощью индукции можно доказать, что любая целая сумма долларов, большая или равная 12, может быть образована комбинацией таких монет. Пусть S ( k ) обозначает утверждение « k долларов можно образовать из комбинации 4- и 5-долларовых монет». Доказательство того, что S ( k ) верно для всех k ≥ 12, может быть получено индукцией по k следующим образом:

Базовый случай: показать, что S ( k ) выполняется для k = 12, просто: возьмите три монеты по 4 доллара.

Шаг индукции: учитывая, что S ( k ) выполняется для некоторого значения k ≥ 12 ( гипотеза индукции ), докажите, что S ( k + 1) тоже выполняется. Предположим, что S ( k ) верно для некоторого произвольного k ≥ 12 . Если существует решение для k долларов, которое включает хотя бы одну монету номиналом 4 доллара, замените ее монетой номиналом 5 долларов, чтобы получить k + 1 доллар. В противном случае, если используются только монеты номиналом 5 долларов, k должно быть кратно 5 и, следовательно, не менее 15; но тогда мы можем заменить три монеты по 5 долларов на четыре монеты по 4 доллара, чтобы получить k + 1 доллар. В каждом случае S ( k + 1) верно.

Следовательно, по принципу индукции S ( k ) выполняется для всех k ≥ 12 , и доказательство завершено.

В этом примере, хотя S ( k ) также имеет место для ${\textstyle k\in \{4,5,8,9,10\}}$, приведенное выше доказательство не может быть изменено для замены минимальной суммы в 12 долларов на любое меньшее значение m . Для m = 11 базовый случай фактически неверен; для m = 10 второй случай на этапе индукции (замена трех монет размером 5 на четыре монеты номиналом 4 доллара) не сработает; не говоря уже о еще более низких m .

Индукция более чем на одном счетчике

Иногда желательно доказать утверждение, включающее два натуральных числа, n и m , путем итерации процесса индукции. То есть доказываются базовый случай и шаг индукции для n , и в каждом из них доказываются базовый случай и шаг индукции для m . См., например, доказательство коммутативности , сопровождающее сложение натуральных чисел . Возможны также более сложные аргументы, включающие три и более счетчиков.

Бесконечный спуск

Основная статья: Бесконечный спуск

Метод бесконечного спуска — это разновидность математической индукции, которую использовал Пьер де Ферма . Он используется, чтобы показать, что некоторое утверждение Q ( n ) неверно для всех натуральных чисел n . Его традиционная форма состоит в том, чтобы показать, что если Q ( n ) верно для некоторого натурального числа n , то оно справедливо и для некоторого строго меньшего натурального числа m . Поскольку не существует бесконечных убывающих последовательностей натуральных чисел, такая ситуация была бы невозможна, тем самым показывая ( от противного ), что Q ( n ) не может быть истинным для любого n .

В справедливости этого метода можно убедиться, исходя из обычного принципа математической индукции. Используя математическую индукцию для утверждения P ( n ), определенного как « Q ( m ) , неверно для всех натуральных чисел m, меньших или равных n », из этого следует, что P ( n ) выполняется для всех n , что означает, что Q ( n ) неверно для любого натурального числа n .

индукция

Если кто-то хочет доказать, что свойство P справедливо для всех натуральных чисел, меньших или равных n , достаточно доказать, что P удовлетворяет следующим условиям:

1. P имеет место для 0,
2. Для любого натурального числа x меньше n , если P выполняется для x , то P выполняется для x + 1.

Префиксная индукция

Наиболее распространенная форма доказательства методом математической индукции требует доказательства на этапе индукции, что

$$\forall k\,(P(k)\to P(k+1))$$

после чего принцип индукции «автоматизирует» n применений этого шага для перехода от P (0) к P ( n ) . Это можно назвать «индукцией предшественника», потому что каждый шаг доказывает что-то о числе на основе чего-то о предшественнике этого числа.

Интересным вариантом вычислительной сложности является «префиксная индукция», при которой на этапе индукции доказывается следующее утверждение:

$$\forall k\,(P(k)\to P(2k)\land P(2k+1))$$

или эквивалентно

$$\forall k\,\left(P\!\left(\left\lfloor {\frac {k}{2}}\right\rfloor \right)\to P(k)\right)$$

Затем принцип индукции «автоматизирует» log ₂   n применений этого вывода для перехода от P (0) к P ( n ) . Фактически, это называется «префиксной индукцией», потому что каждый шаг доказывает что-то о числе на основе чего-то о «префиксе» этого числа, сформированном путем усечения младшего бита его двоичного представления . Это также можно рассматривать как применение традиционной индукции по длине этого двоичного представления.

Если традиционная индукция предшественников интерпретируется вычислительно как n- шаговый цикл, то префиксная индукция будет соответствовать логарифмическому циклу . По этой причине доказательства с использованием префиксной индукции «более конструктивны», чем доказательства с использованием индукции предшественников.

Индукция предшественника может тривиально моделировать префиксную индукцию по тому же утверждению. Префиксная индукция может имитировать индукцию предшественника, но только за счет усложнения синтаксиса утверждения (добавление ограниченного квантора универсальности ), поэтому интересные результаты, связывающие префиксную индукцию с вычислениями за полиномиальное время , зависят от полного исключения неограниченных кванторов и ограничения чередования. ограниченных универсальных и экзистенциальных кванторов, разрешенных в этом утверждении.

Можно пойти еще дальше: нужно доказать

$$\forall k\,\left(P\!\left(\left\lfloor {\sqrt {k}}\right\rfloor \right)\to P(k)\right)$$

после чего принцип индукции «автоматизирует» log log n применения этого вывода при переходе от P (0) к P ( n ) . Аналогично эта форма индукции использовалась для изучения параллельных вычислений с лог-временем.

Полная (

Другой вариант, называемый полной индукцией , курсом индукции значений или сильной индукцией (в отличие от которого базовую форму индукции иногда называют слабой индукцией ), упрощает доказательство шага индукции с помощью более сильной гипотезы: доказывается утверждение $P(m+1)$ в предположении, что $P(n)$ справедливо для всех натуральных чисел $n$ меньше, чем $m+1$; напротив, основная форма предполагает только $P(m)$. Название «сильная индукция» не означает, что этот метод может доказать больше, чем «слабая индукция», а просто относится к более сильной гипотезе, используемой на этапе индукции.

Фактически, можно показать, что эти два метода фактически эквивалентны, как объяснено ниже. В этой форме полной индукции все равно необходимо доказать базовый случай: $P(0)$, и может даже потребоваться доказать внеосновные случаи, такие как $P(1)$ прежде чем будет применен общий аргумент, как в приведенном ниже примере числа Фибоначчи. $F_{n}$.

Хотя только что описанная форма требует доказательства базового случая, в этом нет необходимости, если можно доказать $P(m)$ (при условии $P(n)$ для всех нижних $n$) для всех $m\geq 0$. Это частный случай трансфинитной индукции , описанный ниже, хотя он больше не эквивалентен обычной индукции. В этой форме базовый случай включается в состав случая $m=0$, где $P(0)$ доказано ничем другим $P(n)$ предполагалось; этот случай, возможно, придется рассматривать отдельно, но иногда тот же аргумент применим и для $m=0$ и $m>0$, что делает доказательство более простым и элегантным.Однако в этом методе крайне важно гарантировать, что доказательство $P(m)$ не предполагает безоговорочно, что $m>0$, например, сказав «выберите произвольный $n<m$", или предположив, что в наборе из m элементов есть элемент.

с

Полная индукция эквивалентна обычной математической индукции, описанной выше, в том смысле, что доказательство одним методом может быть преобразовано в доказательство другим методом. Предположим, есть доказательство $P(n)$ путем полной индукции. Затем это доказательство можно преобразовать в обычное индукционное доказательство, приняв более сильную индуктивную гипотезу. Позволять $Q(n)$ быть заявлением " $P(m)$ держится для всех $m$ такой, что $0\leq m\leq n$«— это становится индуктивной гипотезой для обычной индукции. Тогда мы можем показать $Q(0)$ и $Q(n+1)$ для $n\in \mathbb {N}$ предполагая только $Q(n)$ и покажи это $Q(n)$ подразумевает $P(n)$.

Если, с другой стороны, $P(n)$ если бы доказательство было доказано обычной индукцией, то фактически доказательство уже было бы доказательством полной индукции: $P(0)$ доказывается в базовом случае без каких-либо предположений и $P(n+1)$ доказывается на этапе индукции, на котором можно предположить все предыдущие случаи, но достаточно использовать только случай $P(n)$.

Пример: числа Фибоначчи

Полная индукция наиболее полезна, когда для каждого шага индукции требуется несколько экземпляров индуктивной гипотезы. Например, полную индукцию можно использовать, чтобы показать, что

$$F_{n}={\frac {\varphi ^{n}-\psi ^{n}}{\varphi -\psi }}$$

где $F_{n}$ — n- е число Фибоначчи , а ${\textstyle \varphi ={\frac {1}{2}}(1+{\sqrt {5}})}$ ( золотое сечение ) и ${\textstyle \psi ={\frac {1}{2}}(1-{\sqrt {5}})}$ являются корнями многочлена ​ $x^{2}-x-1$. Используя тот факт, что $F_{n+2}=F_{n+1}+F_{n}$ для каждого $n\in \mathbb {N}$, тождество выше можно проверить прямым вычислением для ${\textstyle F_{n+2}}$ если предположить, что это уже справедливо для обоих ${\textstyle F_{n+1}}$ и ${\textstyle F_{n}}$. Для завершения доказательства личность должна быть подтверждена в двух базовых случаях: $n=0$ и ${\textstyle n=1}$.

Пример: факторизация простых чисел

Другое доказательство методом полной индукции использует гипотезу о том, что утверждение справедливо для всех меньших $n$ более тщательно. Рассмотрим утверждение о том, что «каждое натуральное число больше 1 является произведением (одного или нескольких) простых чисел », которое является « существования частью » фундаментальной теоремы арифметики . Для доказательства шага индукции гипотеза индукции состоит в том, что для данного $n>1$ утверждение справедливо для всех меньших $n>1$. Если $m$ является простым, то оно заведомо является произведением простых чисел, а если нет, то по определению это произведение: $m=n_{1}n_{2}$, где ни один из множителей не равен 1; следовательно, ни один из них не равен $m$, и поэтому оба они больше 1 и меньше $m$. Гипотеза индукции теперь применима к $n_{1}$ и $n_{2}$, поэтому каждое из них является произведением простых чисел. Таким образом $m$ является продуктом произведений простых чисел и, следовательно, в более широком смысле является произведением простых чисел.

Пример: пересмотр сумм в долларах

Мы попытаемся доказать тот же пример, что и выше , на этот раз с помощью сильной индукции . Заявление остается прежним:

$$S(n):\,\,n\geq 12\implies \,\exists \,a,b\in \mathbb {N} .\,\,n=4a+5b$$

Однако будут небольшие различия в структуре и предположениях доказательства, начиная с расширенного базового случая.

Доказательство.

Базовый вариант: покажите это $S(k)$ держится за $k=12,13,14,15$.

$${\begin{aligned}4\cdot 3+5\cdot 0=12\\4\cdot 2+5\cdot 1=13\\4\cdot 1+5\cdot 2=14\\4\cdot 0+5\cdot 3=15\end{aligned}}$$

Базовый случай сохраняется.

Индукционный шаг: Учитывая некоторые $j>15$, предполагать $S(m)$ держится для всех $m$ с $12\leq m<j$. Докажите, что $S(j)$ держит.

Выбор $m=j-4$, и наблюдая за этим $15<j\implies 12\leq j-4<j$ показывает, что $S(j-4)$ выполняется по индуктивному предположению. То есть сумма $j-4$ может быть образовано некоторым сочетанием $4$ и $5$ долларовые монеты. Затем, просто добавив $4$ долларовая монета к этой комбинации дает сумму $j$. То есть, $S(j)$ держит КЭД

Индукция вперед-назад

Основная статья: Индукция вперед-назад

Иногда удобнее сделать обратный вывод, доказывая утверждение для $n-1$, учитывая его справедливость для $n$. Однако доказательства достоверности утверждения ни для одного числа недостаточно, чтобы установить базовый случай; вместо этого нужно доказать утверждение для бесконечного подмножества натуральных чисел. Например, Огюстен Луи Коши впервые применил прямую (регулярную) индукцию, чтобы доказать неравенство средних арифметических и геометрических для всех степеней 2 , а затем использовал обратную индукцию, чтобы показать это для всех натуральных чисел.

Пример ошибки на этапе индукции

Основная статья: Все лошади одного цвета

Шаг индукции необходимо доказать для всех значений n . Чтобы проиллюстрировать это, Джоэл Э. Коэн предложил следующий аргумент, целью которого является доказать с помощью математической индукции, что все лошади одного цвета :

Базовый вариант: в наборе всего одна лошадь, только один окрас.

Шаг индукции: в качестве гипотезы индукции предположим, что в любом наборе $n$ Лошади, есть только один цвет. Теперь посмотрим на любой набор $n+1$ лошади. Пронумеруйте их: $1,2,3,\dotsc ,n,n+1$. Рассмотрим множества ${\textstyle \left\{1,2,3,\dotsc ,n\right\}}$ и ${\textstyle \left\{2,3,4,\dotsc ,n+1\right\}}$. Каждый представляет собой набор только $n$ лошадей, поэтому внутри каждой только один цвет. Но эти два набора перекрываются, поэтому среди всех должен быть только один цвет. $n+1$ лошади.

Базовый случай $n=1$ тривиально, и шаг индукции корректен во всех случаях $n>1$. Однако аргумент, использованный на этапе индукции, неверен для $n+1=2$, поскольку утверждение о том, что «два множества перекрываются», неверно для ${\textstyle \left\{1\right\}}$ и ${\textstyle \left\{2\right\}}$.

Формализация

В логике второго порядка можно записать « аксиому индукции» следующим образом:

$$\forall P\,{\Bigl (}P(0)\land \forall k{\bigl (}P(k)\to P(k+1){\bigr )}\to \forall n\,{\bigl (}P(n){\bigr )}{\Bigr )},$$

где P (·) — переменная для предикатов, включающих одно натуральное число, а k и n — переменные для натуральных чисел .

Другими словами, базовый случай P (0) и шаг индукции (а именно, что из гипотезы индукции P ( k ) следует P ( k + 1) ) вместе подразумевают, что P ( n ) для любого натурального числа n . Аксиома индукции утверждает справедливость вывода о том, что P ( n ) выполняется для любого натурального числа n из базового случая и шага индукции.

Первый квантор аксиомы распространяется на предикаты, а не на отдельные числа. Это квантор второго порядка, а это значит, что данная аксиома сформулирована в логике второго порядка . Аксиоматизация арифметической индукции в логике первого порядка требует схемы аксиом, содержащей отдельную аксиому для каждого возможного предиката. В статье «Аксиомы Пеано» содержится дальнейшее обсуждение этого вопроса.

Аксиома структурной индукции для натуральных чисел была впервые сформулирована Пеано, который использовал ее для определения натуральных чисел вместе со следующими четырьмя другими аксиомами:

1. 0 – натуральное число.
2. Функция-преемник s каждого натурального числа дает натуральное число ( s ( x ) = x + 1) .
3. Функция-преемник инъективна .
4. не находится в диапазоне s 0 .

В первого порядка теории множеств ZFC количественная оценка предикатов не допускается, но все же можно выразить индукцию путем количественной оценки множеств:

$$\forall A{\Bigl (}0\in A\land \forall k\in \mathbb {N} {\bigl (}k\in A\to (k+1)\in A{\bigr )}\to \mathbb {N} \subseteq A{\Bigr )}$$

A можно читать как набор, представляющий предложение и содержащий натуральные числа, для которых это предложение справедливо. Это не аксиома, а теорема, учитывая, что натуральные числа определяются на языке теории множеств ZFC аксиомами, аналогичными аксиомам Пеано. См. построение натуральных чисел с использованием аксиомы бесконечности и схемы аксиом спецификации .

Трансфинитная индукция

Основная статья: Трансфинитная индукция

Один из вариантов принципа полной индукции можно обобщить для утверждений об элементах любого обоснованного множества , то есть множества с иррефлексивным отношением <, которое не содержит бесконечных нисходящих цепей . Всякое множество, представляющее порядковое число , обосновано, множество натуральных чисел является одним из них.

Применительно к хорошо обоснованному набору трансфинитная индукция может быть сформулирована как один шаг. Чтобы доказать, что утверждение P ( n ) справедливо для каждого порядкового числа:

1. Покажите для каждого порядкового числа n , что если P ( m ) выполняется для всех m < n , то P ( n ) также выполняется.

Эта форма индукции, примененная к набору порядковых чисел (которые образуют хорошо упорядоченный и, следовательно, обоснованный класс ), называется трансфинитной индукцией . Это важный метод доказательства в теории множеств , топологии и других областях.

Доказательства методом трансфинитной индукции обычно различают три случая:

1. когда n — минимальный элемент, т.е. нет элемента меньше n ;
2. когда n имеет прямого предшественника, т.е. набор элементов, меньших n, имеет наибольший элемент;
3. когда n не имеет прямого предшественника, т. е. n является так называемым предельным порядковым номером .

Строго говоря, при трансфинитной индукции нет необходимости доказывать базовый случай, потому что это пустой частный случай утверждения о том, что если P истинно для всех n < m , то P истинно для m . Это абсурдно верно именно потому, что не существует значений n < m , которые могли бы служить контрпримерами. Таким образом, частные случаи являются частными случаями общего случая.

принципом

Принцип математической индукции обычно формулируется как аксиома натуральных чисел; см. аксиомы Пеано . Он строго сильнее принципа хорошего порядка в контексте других аксиом Пеано. Предположим следующее:

• Аксиома трихотомии : для любых натуральных чисел n и m n тогда меньше или равно m и только тогда, когда m не меньше n .
• Для любого натурального n числа n 1 больше n . +
• Для любого натурального числа n ни одно натуральное число не находится между n и n + 1 .
• Никакое натуральное число не меньше нуля.

Тогда можно доказать, что индукция, учитывая перечисленные выше аксиомы, влечет за собой принцип хорошего порядка. Следующее доказательство использует полную индукцию и первую и четвертую аксиомы.

Доказательство. Предположим, что существует непустое множество S натуральных чисел, не имеющее наименьшего элемента. Пусть P ( n ) — утверждение, что не принадлежит S. n Тогда P (0) истинно, поскольку если бы оно было ложным, то 0 был бы наименьшим элементом S . Более того, пусть n — натуральное число и предположим, что P ( m ) верно для всех натуральных чисел m меньше n + 1 . Тогда, если P ( n + 1) ложно, n + 1 находится в S и, таким образом, является минимальным элементом в S , противоречие. Таким образом, P ( n + 1) истинно. Следовательно, по принципу полной индукции P ( n ) выполняется для всех натуральных чисел n ; поэтому S пусто, противоречие. КЭД

« Цифровая линия » для набора {(0, n ): n ∈ N } ∪ {(1, п ): п € N } . Числа относятся ко второму компоненту пар; первое можно получить по цвету или местоположению.

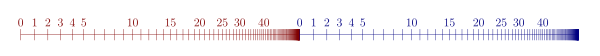
С другой стороны, набор $\{(0,n):n\in \mathbb {N} \}\cup \{(1,n):n\in \mathbb {N} \}$, изображенный на рисунке, является упорядоченным в лексикографическом порядке .Более того, за исключением аксиомы индукции, он удовлетворяет всем аксиомам Пеано, где константа Пеано 0 интерпретируется как пара (0, 0), а функция- преемник Пеано определяется на парах по формуле succ( x , n ) = ( x , n + 1) для всех $x\in \{0,1\}$ и $n\in \mathbb {N}$.В качестве примера нарушения аксиомы индукции определите предикат P ( x , n ) как ( x , n ) = (0, 0) или ( x , n ) = succ( y , m ) для некоторых $y\in \{0,1\}$ и $m\in \mathbb {N}$. Тогда базовый случай P (0, 0) тривиально верен, как и шаг индукции: если P ( x , n ) , то P (succ( x , n ) ) . Однако P не верно для всех пар в наборе.

Аксиомы Пеано с принципом индукции однозначно моделируют натуральные числа. Замена принципа индукции принципом хорошего порядка позволяет создавать более экзотические модели, удовлетворяющие всем аксиомам.

Оно ошибочно напечатано в нескольких книгах. и источники, что принцип хорошего порядка эквивалентен аксиоме индукции. В контексте других аксиом Пеано это не так, но в контексте других аксиом они эквивалентны; в частности, принцип хорошего порядка подразумевает аксиому индукции в контексте первых двух перечисленных выше аксиом и

• Каждое натуральное число равно либо 0, либо n + 1 для некоторого натурального числа n .

Распространенной ошибкой во многих ошибочных доказательствах является предположение, что n − 1 — уникальное и четко определенное натуральное число, свойство, которое не подразумевается другими аксиомами Пеано.

См. также

• Комбинаторное доказательство
• Индукционные головоломки
• Доказательство исчерпанием
• Рекурсия
• Рекурсия (информатика)
• Структурная индукция
• Трансфинитная индукция

Ссылки

Введение

• Франклин, Дж .; Дауд, А. (2011). Доказательство по математике: Введение . Сидней: Книги Кью. ISBN  978-0-646-54509-7 . (Гл. 8.)
• «Математическая индукция» . Энциклопедия математики . ЭМС Пресс . 2001 [1994].
• Гермес, Ганс (1973). Введение в математическую логику . Hochschultext. Лондон: Спрингер. ISBN  978-3540058199 . ISSN   1431-4657 . МР   0345788 .
• Кнут, Дональд Э. (1997). Искусство компьютерного программирования, Том 1: Фундаментальные алгоритмы (3-е изд.). Аддисон-Уэсли. ISBN  978-0-201-89683-1 . (Раздел 1.2.1: Математическая индукция, стр. 11–21.)
• Колмогоров Андрей Н. ; Фомин, Сергей В. (1975). Вводный реальный анализ . Сильверман, Р.А. (пер., ред.). Нью-Йорк: Дувр. ISBN  978-0-486-61226-3 . (Раздел 3.8: Трансфинитная индукция, стр. 28–29.)

История

• Ачерби, Фабио (август 2000 г.). «Платон: Парменид 149a7-c3. Доказательство путем полной индукции?» . Архив истории точных наук . 55 (1): 57–76. дои : 10.1007/s004070000020 . JSTOR   41134098 . S2CID   123045154 .
• Басси, штат Вашингтон (1917). «Происхождение математической индукции». Американский математический ежемесячник . 24 (5): 199–207. дои : 10.2307/2974308 . JSTOR   2974308 .
• Каджори, Флориан (1918). «Происхождение названия «Математическая индукция» ». Американский математический ежемесячник . 25 (5): 197–201. дои : 10.2307/2972638 . JSTOR   2972638 .
• Фаулер, Д. (1994). «Могли ли греки использовать математическую индукцию? Использовали ли они ее?». Физика . 31 : 253–265.
• Фрейденталь, Ганс (1953). «К истории полной индукции». Международные архивы истории наук . 6 :17–37.
• Кац, Виктор Дж. (1998). История математики: Введение . Аддисон-Уэсли . ISBN  0-321-01618-1 .
• Пирс, Чарльз Сандерс (1881). «О логике числа» . Американский журнал математики . 4 (1–4): 85–95. дои : 10.2307/2369151 . JSTOR   2369151 . МР   1507856 . Перепечатано (CP 3.252–288), (W 4:299–309).
• Рабинович, Нахум Л. (1970). «Раввин Леви Бен Гершон и истоки математической индукции». Архив истории точных наук . 6 (3): 237–248. дои : 10.1007/BF00327237 . МР   1554128 . S2CID   119948133 .
• Рашид, Рошди (1972). «Математическая индукция: аль-Караджи, ас-Самаваль». Архив истории точных наук (на французском языке). 9 (1): 1–21. дои : 10.1007/BF00348537 . МР   1554160 . S2CID   124040444 .
• Рашид, Р. (1994). «Математическая индукция: аль-Караджи и аль-Самаваль». Развитие арабской математики: между арифметикой и алгеброй . Бостонские исследования в области философии науки. Том. 156. Springer Science & Business Media. ISBN  9780792325659 .
• Шилдс, Пол (1997). «Аксиоматизация арифметики Пирса». В Хаузере, Натан; Робертс, Дон Д.; Эвра, Джеймс Ван (ред.). Исследования по логике Чарльза С. Пирса . Издательство Университета Индианы. стр. 43–52. ISBN  0-253-33020-3 . МР   1720827 .
• Симонсон, Чарльз Г. (зима 2000 г.). «Математика Леви бен Гершона, Ралбага» (PDF) . Бехол Дерахеха Даеху . 10 . Издательство Университета Бар-Илан: 5–21.
• Унгуру, С. (1991). «Греческая математика и математическая индукция». Физика . 28 : 273–289.
• Унгуру, С. (1994). «Детская охота после индукции». Физика . 31 : 267–272.
• Вакка, Г. (1909). «Мавролик, первый открыватель принципа математической индукции» . Бюллетень Американского математического общества . 16 (2): 70–73. дои : 10.1090/S0002-9904-1909-01860-9 . МР   1558845 .
• Ядегари, Мохаммад (1978). «Использование математической индукции Абу Камилом Шуджой ибн Асламом (850–930)». Исида . 69 (2): 259–262. дои : 10.1086/352009 . JSTOR   230435 . S2CID   144112534 .