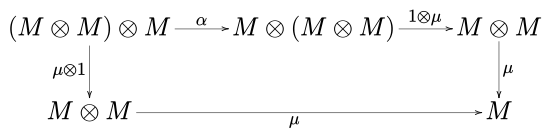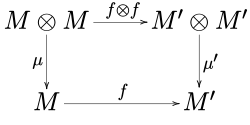Моноид (теория категорий)

В теории категорий , разделе математики , моноид (или моноидный объект , или внутренний моноид , или алгебра ) ( M , µ , η ) в моноидальной категории ( C , ⊗, I ) представляет собой объект M вместе с двумя морфизмами.

µ : M ⊗ M → M называется умножением ,
η : I → M называется единицей ,

такая, что пятиугольная диаграмма

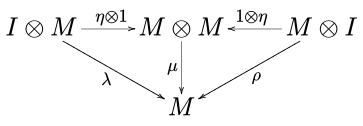
и диаграмма юнитора

добираться . В приведенных выше обозначениях 1 — тождественный морфизм M α , I единичный элемент, а , λ и ρ — соответственно ассоциативность, левая идентичность и правая идентичность моноидальной категории C. —

Двойственным образом комоноид в моноидальной категории C является моноидом в двойственной категории C. ^на.

Предположим, что моноидальная категория C обладает симметрией γ . Моноид M в C коммутативен , когда µ ∘ γ = µ .

Примеры [ править ]

Моноидный объект в Set , категории множеств (с моноидальной структурой, индуцированной декартовым произведением ), является моноидом в обычном смысле.
Моноидный объект в Top , категории топологических пространств (с моноидальной структурой, индуцированной топологией произведения ), является топологическим моноидом .
Моноидный объект в категории моноидов (с прямым произведением моноидов) — это просто коммутативный моноид . Это легко следует из аргумента Экмана–Хилтона .
Моноидный объект в категории полных соединений-полурешеток Sup (с моноидальной структурой, индуцированной декартовым произведением) является единичным кванталом .
Моноидный объект в ( Ab , ⊗ _Z , Z ) , категории абелевых групп , является кольцом .
Для коммутативного кольца R моноидный объект в
- ( R - Mod , ⊗ _R , R ) , категория модулей над R , является R -алгеброй .
- категория градуированных модулей есть градуированная R -алгебра .
- категория цепных комплексов - модулей R является дифференциально-градуированной алгеброй .
Моноидный объект в K - Vect , категории K -векторных пространств (опять же, с тензорным произведением), является унитарной ассоциативной K - алгеброй , а комоноидный объект является K - коалгеброй .
Для любой категории C категория [ C , C ] ее эндофункторов индуцированную композицией и тождественным функтором I _C. имеет моноидальную структуру , Моноидный объект [ C , C ] является монадой на C. в
Для любой категории с терминальным объектом и конечными произведениями каждый объект становится комоноидным объектом посредством диагонального морфизма Δ _X : X → X × X . Двойственным образом в категории с исходным объектом и конечными копроизведениями каждый объект становится моноидным объектом через id _X ⊔ id _X : X ⊔ X → X .

Категории моноидов [ править ]

Учитывая два моноида ( M , µ , η ) и ( M ′, µ ′, η ′) в моноидальной категории C , морфизм f : M → M ′ является морфизмом моноидов , когда

ж ∘ µ знак равно µ ′ ∘ ( ж ⊗ ж ),
ж ∘ η = η ′.

Другими словами, следующие диаграммы

,

добираться.

Категория моноидов в C и их моноидных морфизмов обозначается Mon _C . ^[1]

См. также [ править ]

Act-S , категория моноидов, действующих на множествах

Ссылки [ править ]

^ Раздел VII.3 в Мак Лейн, Сондерс (1988). Категории для работающего математика (4-е корр. печат. изд.). Нью-Йорк: Springer-Verlag. ISBN 0-387-90035-7 .

Килп, Мати; Кнауэр, Ульрих; Михалов, Александр В. (2000). Моноиды, акты и категории . Вальтер де Грюйтер. ISBN 3-11-015248-7 .

[1] Раздел VII.3 в Мак Лейн, Сондерс (1988). Категории для работающего математика (4-е корр. печат. изд.). Нью-Йорк: Springer-Verlag. ISBN 0-387-90035-7 .

[1]