Пупочная точка

Линии кривизны эллипсоида, показывающие точки пуповины (красные).

В поверхностей дифференциальной геометрии трехмерных омбилики или омбилические точки — это точки на поверхности, которые являются локально сферическими. В таких точках нормальные кривизны во всех направлениях равны, следовательно, обе главные кривизны равны, и каждый касательный вектор является главным направлением . Название «пупок» происходит от латинского umbilicus ( пупок ).

Точки пупка обычно встречаются как изолированные точки в эллиптической области поверхности; то есть там, где гауссова кривизна положительна.

Нерешенная задача по математике :

Имеет ли каждая гладкая топологическая сфера в евклидовом пространстве хотя бы две омбилики?

(еще нерешенные задачи по математике)

Сфера . — единственная поверхность с ненулевой кривизной, каждая точка которой является омбилической Плоский омбилик — это омбилик с нулевой гауссовой кривизной. — Седло обезьяны это пример поверхности с плоской пуповиной, а каждая точка на плоскости является плоской пуповиной. Замкнутая поверхность, топологически эквивалентная тору, может иметь или не иметь нулевые омбилики, но каждая замкнутая поверхность ненулевой эйлеровой характеристики , гладко вложенная в евклидово пространство , имеет хотя бы одну омбилику. Недоказанная гипотеза Константина Каратеодори утверждает, что каждая гладкая поверхность, топологически эквивалентная сфере, имеет по крайней мере две пуповины. ^[1]

Тремя основными типами омбиликов являются эллиптические омбилики, параболические омбилики и гиперболические омбилики. Эллиптические шлангокабели имеют три гребневые линии, проходящие через пупок, а гиперболические шлангокабели имеют только одну. Параболические омбилики представляют собой переходный случай с двумя гребнями, один из которых является особым. Для переходных случаев возможны и другие конфигурации. Эти случаи соответствуют D ₄⁻, Д ₅ и Д ₄⁺ Рене Тома элементарные катастрофы теории катастроф .

Шланги также можно охарактеризовать рисунком поля вектора главного направления вокруг пуповины, которое обычно образует одну из трех конфигураций: звезда, лимон и лимонная звезда (или монстар). Индекс . векторного поля равен либо −½ (звезда), либо ½ (лимон, монстар) Эллиптические и параболические шлангокабели всегда имеют звездчатый рисунок, тогда как гиперболические шлангокабели могут быть звездчатыми, лимонными или монстарными. Эта классификация была впервые предложена Дарбу , а имена взяты из Ханнея. ^[2]

Для поверхностей рода 0 с изолированными омбиликами, например эллипсоида, индекс векторного поля главного направления должен быть равен 2 по теореме Пуанкаре – Хопфа . Типовые поверхности рода 0 имеют как минимум четыре пуповины с индексом ½. Эллипсоид вращения имеет две нетиповые омбилики, каждая из которых имеет индекс 1. ^[3]

конфигурации линий кривизны вблизи шлангокабелей
Звезда
Монстар
Лимон

Классификация шлангокабелей

Кубические формы

Классификация пуповин тесно связана с классификацией действительных кубических форм. $ax^{3}+3bx^{2}y+3cxy^{2}+dy^{3}$ . Кубическая форма будет иметь несколько корневых линий. $\lambda (x,y)$ такая, что кубическая форма равна нулю для всех действительных $\lambda$ . Существует ряд возможностей, в том числе:

Три четкие линии: эллиптическая кубическая форма , стандартная модель. $x^{2}y-y^{3}$ .
Три линии, две из которых совпадают: параболическая кубическая форма , стандартная модель. $x^{2}y$ .
Одна действительная линия: гиперболическая кубическая форма , стандартная модель. $x^{2}y+y^{3}$ .
Три совпадающие линии, стандартная модель $x^{3}$ . ^[4]

Классы эквивалентности таких кубик при равномерном масштабировании образуют трехмерное реальное проективное пространство, а подмножество параболических форм определяет поверхность, названную браслетом пупочным Кристофером Зееманом . ^[4] Принятие классов эквивалентности при вращении системы координат удаляет еще один параметр, и кубические формы могут быть представлены комплексной кубической формой. $z^{3}+3{\overline {\beta }}z^{2}{\overline {z}}+3\beta z{\overline {z}}^{2}+{\overline {z}}^{3}$ с одним комплексным параметром $\beta$ . Параболические формы возникают, когда $\beta ={\tfrac {1}{3}}(2e^{i\theta }+e^{-2i\theta })$ , внутренняя дельтовидная, эллиптическая формы находятся внутри дельтовидной, а гиперболическая – снаружи. Если $\left|\beta \right|=1$ и $\beta$ не является кубическим корнем из единицы, то кубическая форма является прямоугольной кубической формой , которая играет особую роль для шлангокабелей. Если $\left|\beta \right|={\tfrac {1}{3}}$ тогда две корневые линии ортогональны. ^[5]

Вторая кубическая форма, якобиан, формируется путем взятия определителя якобиана векторной функции. $F:\mathbb {R} ^{2}\rightarrow \mathbb {R} ^{2}$ , $F(x,y)=(x^{2}+y^{2},ax^{3}+3bx^{2}y+3cxy^{2}+dy^{3})$ . С точностью до постоянного кратного это кубическая форма. $bx^{3}+(2c-a)x^{2}y+(d-2b)xy^{2}-cy^{3}$ . Используя комплексные числа, якобиан представляет собой параболическую кубическую форму, когда $\beta =-2e^{i\theta }-e^{-2i\theta }$ , внешняя дельтовидная мышца на классификационной схеме. ^[5]

Пупочная классификация

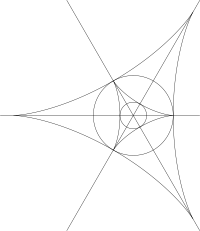
Любая поверхность с изолированной омбилической точкой в начале координат может быть выражена как формы Монжа. параметризация $z={\tfrac {1}{2}}\kappa (x^{2}+y^{2})+{\tfrac {1}{3}}(ax^{3}+3bx^{2}y+3cxy^{2}+dy^{3})+\ldots$ , где $\kappa$ – единственная главная кривизна. Тип пуповины классифицируется по кубической форме из кубической части и соответствующей якобианской кубической формы. Хотя основные направления не определены однозначно на шлангокабеле, можно найти пределы главных направлений при следовании по гребню на поверхности, и они соответствуют корневым линиям кубической формы. Характер линий кривизны определяется якобианом. ^[5]

Классификация пупочных точек следующая: ^[5]

Внутренняя часть внутренней дельтовидной мышцы – эллиптические пупки.
- На внутренней окружности - две касательные линии гребня.
На внутренней дельтовидной мышце – параболическая пупочная мышца.
Наружная внутренняя дельтовидная мышца – гиперболическая пупочная мышца.
- Внутри внешнего круга — звездный узор.
- На внешнем круге – рождение пуповины
- Между внешним кругом и внешней дельтовидной мышцей — узор монстар.
- Внешняя внешняя дельтовидная мышца – лимонный узор.
Бугорки внутренней дельтовидной мышцы – кубические (символические) пупки.
По диагоналям и горизонтальной линии — симметричные пуповины с зеркальной симметрией.

В общем семействе поверхностей шлангокабели могут создаваться или разрушаться парами: рождение переходного шлейфа . Оба шлангокабеля будут гиперболическими: один со звездообразным узором, другой с узором в виде монстра. Внешний круг на диаграмме, имеющий прямоугольную кубическую форму, обозначает эти переходные случаи. Символические пуповины представляют собой особый случай. ^[5]

Фокальная поверхность

Эллиптические и гиперболические омбилики имеют совершенно разные фокальные поверхности . Гребень на поверхности соответствует краям возврата, поэтому каждый лист эллиптической фокальной поверхности будет иметь три края возврата, которые сходятся вместе в пупочном фокусе, а затем переключаются на другой лист. У гиперболической пуповины имеется единственное ребро возврата, которое переходит с одного листа на другой. ^[5]

Определение в более высокой размерности в римановых многообразиях

Точка p в римановом подмногообразии является пупочной, если в точке p (векторнозначная) Вторая фундаментальная форма является некоторым нормальным векторным тензором, индуцированной метрикой ( Первая фундаментальная форма ). Эквивалентно, для всех векторов U , V в точке p , II( U , V ) = g _p ( U , V ) $\nu$ , где $\nu$ — вектор средней кривизны в точке p .

Подмногообразие называется омбилическим (или полностью омбилическим), если это условие выполняется в каждой точке «p». Это эквивалентно утверждению, что подмногообразие можно сделать полностью геодезическим путем соответствующего конформного изменения метрики окружающего («окружающего») многообразия. Например, поверхность в евклидовом пространстве является омбилической тогда и только тогда, когда она является частью сферы.

См. также

пупок - анатомический термин , означающий пупок или относящийся к нему.

Ссылки

^ Бергер, Марсель (2010), «Гипотеза Карадеодори», «Геометрия раскрыта » , Springer, Heidelberg, стр. 389–390, doi : 10.1007/978-3-540-70997-8 , ISBN 978-3-540-70996-1 , МР 2724440 .
^ Берри, М.В.; Ханней, Дж. Х. (1977). «Пуповые точки на гауссовых случайных поверхностях». Дж. Физ. А. 10 (11): 1809–21. Бибкод : 1977JPhA...10.1809B . дои : 10.1088/0305-4470/10/11/009 .
^ Портеус, стр. 208.
^ Jump up to: ^а ^б Постон, Тим ; Стюарт, Ян (1978), Теория катастроф и ее приложения , Питман, ISBN 0-273-01029-8
^ Jump up to: ^а ^б ^с ^д ^и ^ж Портеус, Ян Р. (2001), Геометрическое дифференцирование , Cambridge University Press, стр. 198–213, ISBN 0-521-00264-8

Дарбу, Гастон (1896) [1887], Уроки общей теории поверхностей: тома I–IV , Готье-Виллар
Изображения звезды, лимона, монстара и другие ссылки.

[1] Бергер, Марсель (2010), «Гипотеза Карадеодори», «Геометрия раскрыта » , Springer, Heidelberg, стр. 389–390, doi : 10.1007/978-3-540-70997-8 , ISBN 978-3-540-70996-1 , МР 2724440 .

[2] Берри, М.В.; Ханней, Дж. Х. (1977). «Пуповые точки на гауссовых случайных поверхностях». Дж. Физ. А. 10 (11): 1809–21. Бибкод : 1977JPhA...10.1809B . дои : 10.1088/0305-4470/10/11/009 .

[3] Портеус, стр. 208.

[Poston-4] Jump up to: ^а ^б Постон, Тим ; Стюарт, Ян (1978), Теория катастроф и ее приложения , Питман, ISBN 0-273-01029-8

[Port-5] Jump up to: ^а ^б ^с ^д ^и ^ж Портеус, Ян Р. (2001), Геометрическое дифференцирование , Cambridge University Press, стр. 198–213, ISBN 0-521-00264-8

[1]

[2]

[3]

[4]

[5]