Седло обезьяны

В математике седло обезьяны — это поверхность , определяемая уравнением

z=x^{3}-3xy^{2},\,

или в цилиндрических координатах

z=\rho ^{3}\cos(3\varphi ).

Он принадлежит к классу седловых поверхностей , и его название происходит от наблюдения, что потребует двух седло обезьяны углублений для ног и одного для хвоста. Дело ⁠ $(0,0,0)$ ⁠ на седле обезьяны соответствует вырожденной критической точке функции ⁠ $z(x,y)$ ⁠ в ⁠ $(0,0)$ ⁠ . Седло обезьяны имеет изолированную точку пуповины с нулевой гауссовой кривизной в начале координат, тогда как во всех остальных точках кривизна строго отрицательна.

Можно связать прямоугольные и цилиндрические уравнения, используя комплексные числа. $x+iy=re^{i\varphi }:$

z=x^{3}-3xy^{2}=\operatorname {Re} [(x+iy)^{3}]=\operatorname {Re} [r^{3}e^{3i\varphi }]=r^{3}\cos(3\varphi ).

Заменив 3 в цилиндрическом уравнении любым целым числом ⁠ $k\geq 1,$ ⁠ можно сделать седло из ⁠ $k$ ⁠ депрессии. ^[1]

Другая ориентация седла обезьяны — это лепесток корюшки , определяемый $x+y+z+xyz=0,$ так, чтобы ось z седла обезьяны соответствовала направлению ⁠ $(1,1,1)$ ⁠ в лепестке Корюшки. ^[2]^[3]

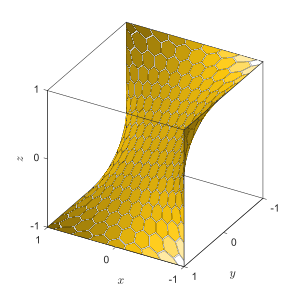
Седло лошади

Термин «лошадиное седло» может использоваться в отличие от седла обезьяны для обозначения обычной поверхности седла, в которой z ( x , y ) имеет седловую точку , локальный минимум или максимум в каждом направлении плоскости xy . Напротив, седло обезьяны имеет стационарную точку перегиба во всех направлениях.

Ссылки

^ Пекхэм, С.Д. (2011) Седла обезьян, морских звезд и осьминогов, Proceedings of Geomorphometry 2011 , Редлендс, Калифорния, стр. 31-34, https://www.researchgate.net/publication/256808897_Monkey_Starfish_and_Octopus_Saddles
^ Дж., Римротт, Ф.П. (1989). Вводная динамика отношения . Нью-Йорк, штат Нью-Йорк: Springer New York. п. 26. ISBN 9781461235026 . OCLC 852789976 . {{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка )
^ Чессер, Х.; Римротт, FPJ (1985). Расмуссен, Х. (ред.). «Треугольник Магнуса и корюшка». CANCAM '85: Материалы Десятого Канадского конгресса прикладной механики, 2–7 июня 1985 г., Университет Западного Онтарио, Лондон, Онтарио, Канада .

Внешние ссылки

Вайсштейн, Эрик В. «Седло обезьяны» . Математический мир .

[1] Пекхэм, С.Д. (2011) Седла обезьян, морских звезд и осьминогов, Proceedings of Geomorphometry 2011 , Редлендс, Калифорния, стр. 31-34, https://www.researchgate.net/publication/256808897_Monkey_Starfish_and_Octopus_Saddles

[2] Дж., Римротт, Ф.П. (1989). Вводная динамика отношения . Нью-Йорк, штат Нью-Йорк: Springer New York. п. 26. ISBN 9781461235026 . OCLC 852789976 . {{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка )

[3] Чессер, Х.; Римротт, FPJ (1985). Расмуссен, Х. (ред.). «Треугольник Магнуса и корюшка». CANCAM '85: Материалы Десятого Канадского конгресса прикладной механики, 2–7 июня 1985 г., Университет Западного Онтарио, Лондон, Онтарио, Канада .

[1]

[2]

[3]