метод Гаусса

В орбитальной механике (раздел небесной механики ) метод Гаусса используется для предварительного определения орбиты на основе как минимум трех наблюдений (большее количество наблюдений увеличивает точность определения орбиты) интересующего тела, вращающегося по орбите, в три разных момента времени. Требуемой информацией являются времена наблюдений, векторы положения точек наблюдения (в экваториальной системе координат ), направляющий косинус-вектор вращающегося тела из точек наблюдения (из топоцентрической экваториальной системы координат) и общие физические данные.

Работая в 1801 году, Карл Фридрих Гаусс разработал важные математические методы (обобщенные в методах Гаусса), которые специально использовались для определения орбиты Цереры . Показанный ниже метод представляет собой определение орбиты вращающегося тела вокруг фокального тела, с которого были сняты наблюдения, тогда как метод определения орбиты Цереры требует немного больше усилий, поскольку наблюдения проводились с Земли, когда Церера вращается вокруг Солнца .

Вектор положения наблюдателя

Вектор положения наблюдателя (в экваториальной системе координат ) точек наблюдения может быть определен по широте и местному звездному времени (из топоцентрической системы координат ) на поверхности фокального тела вращающегося тела (например, Земли) посредством либо :

Геодезическая широта

Геоцентрическая широта

${\begin{aligned}\mathbf {R_{n}} &=\left[{R_{e} \over {\sqrt {1-(2f-f^{2})\sin ^{2}\phi _{n}}}}+H_{n}\right]\cos \phi _{n}(\cos \theta _{n}\ \mathbf {\hat {I}} +\sin \theta _{n}\ \mathbf {\hat {J}} )+\left[{R_{e}(1-f)^{2} \over {\sqrt {1-(2f-f^{2})\sin ^{2}\phi _{n}}}}+H_{n}\right]\sin \phi _{n}\ \mathbf {\hat {K}} \\&=\left[{R_{e} \over {\sqrt {1-e^{2}\sin ^{2}\phi _{n}}}}+H_{n}\right]\cos \phi _{n}(\cos \theta _{n}\ \mathbf {\hat {I}} +\sin \theta _{n}\ \mathbf {\hat {J}} )+\left[{R_{e}(1-e^{2}) \over {\sqrt {1-e^{2}\sin ^{2}\phi _{n}}}}+H_{n}\right]\sin \phi _{n}\ \mathbf {\hat {K}} \end{aligned}}$ или $\mathbf {R_{n}} =r_{e}\cos \phi '_{n}\cos \theta _{n}\ \mathbf {\hat {I}} +r_{e}\cos \phi '_{n}\sin \theta _{n}\ \mathbf {\hat {J}} +r_{e}\sin \phi '_{n}\ \mathbf {\hat {K}}$ где,

$\mathbf {R_{n}}$ - соответствующий вектор положения наблюдателя (в экваториальной системе координат).
$R_{e}$ — экваториальный радиус центрального тела (например, 6378 км для Земли)
$r_{e}$ это геоцентрическое расстояние
$f$ — это сжатие (или уплощение ) центрального тела (например, 0,003353 для Земли)
$e$ — эксцентриситет центрального тела (например, 0,081819 для Земли)
$\phi _{n}$ - геодезическая широта (угол между нормалью горизонтальной плоскости и экваториальной плоскостью)
$\phi '_{n}$ - геоцентрическая широта (угол между радиусом и экваториальной плоскостью)
$H_{n}$ это геодезическая высота
$\theta _{n}$ местное звездное время места наблюдения

Косинус вектор направления вращения тела

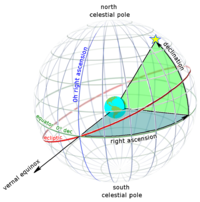
Косинус-вектор направления тела, вращающегося по орбите, можно определить по прямому восхождению и склонению (из топоцентрической экваториальной системы координат) тела, вращающегося по орбите, из точек наблюдения через:

$\mathbf {{\hat {\boldsymbol {\rho }}}_{n}} =\cos \delta _{n}\cos \alpha _{n}\ \mathbf {\hat {I}} +\cos \delta _{n}\sin \alpha _{n}\ \mathbf {\hat {J}} +\sin \delta _{n}\ \mathbf {\hat {K}}$ где,

$\mathbf {{\hat {\boldsymbol {\rho }}}_{n}}$ - соответствующий единичный вектор в направлении вектора положения $\rho$ (от точки наблюдения до тела, вращающегося в топоцентрической экваториальной системе координат)
$\delta _{n}$ соответствующее склонение
$\alpha _{n}$ соответствующее прямое восхождение

Алгоритм

Первоначальный вывод начинается с сложения векторов для определения вектора положения вращающегося тела. Затем на основе сохранения углового момента и принципов кеплеровской орбиты (которые утверждают, что орбита лежит в двумерной плоскости в трехмерном пространстве) устанавливается линейная комбинация указанных векторов положения. Также используется связь между положением тела и вектором скорости коэффициентами Лагранжа , что приводит к использованию указанных коэффициентов. Затем с помощью векторных манипуляций и алгебры были получены следующие уравнения. Подробный вывод см. у Кертиса. ^{[ 1 ]}

ПРИМЕЧАНИЕ. Метод Гаусса представляет собой предварительное определение орбиты с упором на предварительное определение. Аппроксимация коэффициентов Лагранжа и ограничения требуемых условий наблюдения (т. е. незначительная кривизна дуги между наблюдениями см. Гронки ^{[ 2 ]} подробнее) вызывает неточности. Однако метод Гаусса можно улучшить, увеличив точность подкомпонентов, например, решения уравнения Кеплера . Другой способ повысить точность — увеличить количество наблюдений.

Шаг 1

Вычисляем временные интервалы, вычитаем времена между наблюдениями: ${\begin{aligned}\tau _{1}&=t_{1}-t_{2}\\\tau _{3}&=t_{3}-t_{2}\\\tau &=t_{3}-t_{1}\end{aligned}}$ где

$\tau _{n}$ это временной интервал
$t_{n}$ соответствующее время наблюдения

Шаг 2

Вычислите векторные произведения, возьмите векторные произведения направления единицы наблюдения (порядок имеет значение): ${\begin{aligned}\mathbf {p_{1}} &=\mathbf {{\hat {\boldsymbol {\rho }}}_{2}} \times \mathbf {{\hat {\boldsymbol {\rho }}}_{3}} \\\mathbf {p_{2}} &=\mathbf {{\hat {\boldsymbol {\rho }}}_{1}} \times \mathbf {{\hat {\boldsymbol {\rho }}}_{3}} \\\mathbf {p_{3}} &=\mathbf {{\hat {\boldsymbol {\rho }}}_{1}} \times \mathbf {{\hat {\boldsymbol {\rho }}}_{2}} \end{aligned}}$ где

$\mathbf {a} \times \mathbf {b}$ векторное произведение векторов $\mathbf {a} {\text{ and }}\mathbf {b}$
$\mathbf {p_{n}}$ соответствующий вектор векторного произведения
$\mathbf {{\hat {\boldsymbol {\rho }}}_{n}}$ соответствующий единичный вектор

Шаг 3

Вычислите общую скалярную величину (тройное скалярное произведение), возьмите скалярное произведение первого единичного вектора наблюдения на векторное произведение второго и третьего единичных векторов наблюдения:

$D_{0}=\mathbf {{\hat {\boldsymbol {\rho }}}_{1}} \cdot \mathbf {p_{1}} =\mathbf {{\hat {\boldsymbol {\rho }}}_{1}} \cdot (\mathbf {{\hat {\boldsymbol {\rho }}}_{2}} \times \mathbf {{\hat {\boldsymbol {\rho }}}_{3}} )$ где

$\mathbf {a} \cdot \mathbf {b}$ это скалярное произведение векторов $\mathbf {a}$ и $\mathbf {b}$
$D_{0}$ — обычное скалярное тройное произведение
$\mathbf {p_{n}}$ соответствующий вектор векторного произведения
$\mathbf {{\hat {\boldsymbol {\rho }}}_{n}}$ соответствующий единичный вектор

Шаг 4

Рассчитайте девять скалярных величин (аналогично шагу 3): ${\begin{aligned}D_{11}&=\mathbf {R_{1}} \cdot \mathbf {p_{1}} &D_{12}&=\mathbf {R_{1}} \cdot \mathbf {p_{2}} &D_{13}&=\mathbf {R_{1}} \cdot \mathbf {p_{3}} \\D_{21}&=\mathbf {R_{2}} \cdot \mathbf {p_{1}} &D_{22}&=\mathbf {R_{2}} \cdot \mathbf {p_{2}} &D_{23}&=\mathbf {R_{2}} \cdot \mathbf {p_{3}} \\D_{31}&=\mathbf {R_{3}} \cdot \mathbf {p_{1}} &D_{32}&=\mathbf {R_{3}} \cdot \mathbf {p_{2}} &D_{33}&=\mathbf {R_{3}} \cdot \mathbf {p_{3}} \end{aligned}}$ где

$D_{mn}$ — соответствующие скалярные величины
$\mathbf {R_{m}}$ соответствующий вектор положения наблюдателя
$\mathbf {p_{n}}$ соответствующий вектор векторного произведения

Шаг 5

Вычислите скалярные коэффициенты положения:

${\begin{aligned}A&={\frac {1}{D_{0}}}\left(-D_{12}{\frac {\tau _{3}}{\tau }}+D_{22}+D_{32}{\frac {\tau _{1}}{\tau }}\right)\\B&={\frac {1}{6D_{0}}}\left[D_{12}\left(\tau _{3}^{2}-\tau ^{2}\right){\frac {\tau _{3}}{\tau }}+D_{32}\left(\tau ^{2}-\tau _{1}^{2}\right){\frac {\tau _{1}}{\tau }}\right]\\E&=\mathbf {R_{2}} \cdot \mathbf {{\hat {\boldsymbol {\rho }}}_{2}} \end{aligned}}$ где

$A$ , $B$ , и $E$ являются скалярными позиционными коэффициентами
$D_{0}$ — обычная скалярная величина
$D_{mn}$ — соответствующие скалярные величины
$\tau _{n}$ это временной интервал
$R_{n}$ соответствующий вектор положения наблюдателя
$\mathbf {{\hat {\boldsymbol {\rho }}}_{n}}$ соответствующий единичный вектор

Шаг 6

Вычислите квадрат скалярного расстояния второго наблюдения, взяв скалярное произведение вектора положения второго наблюдения: ${R_{2}}^{2}=\mathbf {R_{2}} \cdot \mathbf {R_{2}}$ где

${R_{2}}^{2}$ - квадрат расстояния второго наблюдения
$\mathbf {R_{2}}$ - вектор положения второго наблюдения

Шаг 7

Вычислите коэффициенты скалярного полинома расстояния для второго наблюдения вращающегося тела: ${\begin{aligned}a&=-\left(A^{2}+2AE+{R_{2}}^{2}\right)\\b&=-2\mu B(A+E)\\c&=-\mu ^{2}B^{2}\end{aligned}}$ где

$a{\text{, }}b{\text{, and }}c$ – коэффициенты скалярного полинома расстояния для второго наблюдения вращающегося тела
$A{\text{, }}B{\text{, and }}E$ являются скалярными позиционными коэффициентами
$\mu$ гравитационный параметр фокального тела вращающегося тела

Шаг 8

Найдите корень полинома скалярного расстояния для второго наблюдения вращающегося тела: ${r_{2}}^{8}+a{r_{2}}^{6}+b{r_{2}}^{3}+c=0$ где

$r_{2}$ — скалярное расстояние для второго наблюдения вращающегося тела (оно и его вектор r ₂ находятся в экваториальной системе координат)
$a{\text{, }}b{\text{, and }}c$ являются коэффициентами, как указано ранее

Для нахождения корня можно использовать различные методы, предлагаемый метод — метод Ньютона-Рафсона . Корень должен быть физически возможным (т. е. не отрицательным и не комплексным), и если подходят несколько корней, каждый из них должен быть оценен и сравнен с любыми доступными данными для подтверждения их достоверности.

Шаг 9

Рассчитайте наклонную дальность , расстояние от точки наблюдения до тела, вращающегося по орбите, в соответствующее время: ${\begin{aligned}\rho _{1}&={\frac {1}{D_{0}}}\left[{\frac {6\left(D_{31}{\dfrac {\tau _{1}}{\tau _{3}}}+D_{21}{\dfrac {\tau }{\tau _{3}}}\right){r_{2}}^{3}+\mu D_{31}\left(\tau ^{2}-{\tau _{1}}^{2}\right){\dfrac {\tau _{1}}{\tau _{3}}}}{6{r_{2}}^{3}+\mu \left(\tau ^{2}-{\tau _{3}}^{2}\right)}}-D_{11}\right]\\\rho _{2}&=A+{\frac {\mu B}{{r_{2}}^{3}}}\\\rho _{3}&={\frac {1}{D_{0}}}\left[{\frac {6\left(D_{13}{\dfrac {\tau _{3}}{\tau _{1}}}-D_{23}{\dfrac {\tau }{\tau _{1}}}\right){r_{2}}^{3}+\mu D_{13}\left(\tau ^{2}-{\tau _{3}}^{2}\right){\dfrac {\tau _{3}}{\tau _{1}}}}{6{r_{2}}^{3}+\mu \left(\tau ^{2}-{\tau _{1}}^{2}\right)}}-D_{33}\right]\end{aligned}}$ где

$\rho _{n}$ - соответствующий наклонный диапазон (он и его вектор, $\mathbf {\rho _{n}}$ , находятся в топоцентрической экваториальной системе координат)
$D_{0}$ — обычная скалярная величина
$D_{mn}$ — соответствующие скалярные величины
$\tau _{(n)}$ это временной интервал.
$r_{2}$ - скалярное расстояние для второго наблюдения вращающегося тела
$\mu$ гравитационный параметр фокального тела вращающегося тела

Шаг 10

Вычислите векторы положения вращающегося тела, добавив вектор положения наблюдателя к вектору наклонного направления (который представляет собой наклонное расстояние, умноженное на вектор наклонного направления):

${\begin{aligned}\mathbf {r_{1}} &=\mathbf {R_{1}} +\rho _{1}\mathbf {{\hat {\boldsymbol {\rho }}}_{1}} \\[1.7ex]\mathbf {r_{2}} &=\mathbf {R_{2}} +\rho _{2}\mathbf {{\hat {\boldsymbol {\rho }}}_{2}} \\[1.7ex]\mathbf {r_{3}} &=\mathbf {R_{3}} +\rho _{3}\mathbf {{\hat {\boldsymbol {\rho }}}_{3}} \end{aligned}}$ где

$\mathbf {r_{n}}$ — соответствующий вектор положения вращающегося тела (в экваториальной системе координат ).
$\mathbf {R_{n}}$ соответствующий вектор положения наблюдателя
$\rho _{n}$ соответствующий наклонный диапазон
$\mathbf {{\hat {\boldsymbol {\rho }}}_{n}}$ соответствующий единичный вектор

Шаг 11

Рассчитаем коэффициенты Лагранжа: ${\begin{aligned}f_{1}&\approx 1-{\frac {1}{2}}{\frac {\mu }{{r_{2}}^{3}}}{\tau _{1}}^{2}\\f_{3}&\approx 1-{\frac {1}{2}}{\frac {\mu }{{r_{2}}^{3}}}{\tau _{3}}^{2}\\g_{1}&\approx \tau _{1}-{\frac {1}{6}}{\frac {\mu }{{r_{2}}^{3}}}{\tau _{1}}^{3}\\g_{3}&\approx \tau _{3}-{\frac {1}{6}}{\frac {\mu }{{r_{2}}^{3}}}{\tau _{3}}^{3}\end{aligned}}$ где,

$f_{1}$ , $f_{3}$ , $g_{1}$ и $g_{3}$ – коэффициенты Лагранжа (это лишь первые два члена выражения ряда, основанного на предположении о малом временном интервале)
$\mu$ гравитационный параметр фокального тела вращающегося тела
$r_{2}$ - скалярное расстояние для второго наблюдения вращающегося тела
$\tau _{(n)}$ это временной интервал

Шаг 12

Рассчитаем вектор скорости для второго наблюдения вращающегося тела:

$\mathbf {v_{2}} ={\frac {1}{f_{1}g_{3}-f_{3}g_{1}}}\left(-f_{3}\mathbf {r_{1}} +f_{1}\mathbf {r_{3}} \right)$ где

$\mathbf {v_{2}}$ — вектор скорости для второго наблюдения вращающегося тела (в экваториальной системе координат ).
$f_{1}$ , $f_{3}$ , $g_{1}$ и $g_{3}$ коэффициенты Лагранжа
$\mathbf {r_{n}}$ - соответствующий вектор положения тела на орбите

Шаг 13

Векторы состояния орбиты теперь найдены, вектор положения ( r2 ₎ и скорости ( v2 ₎ для второго наблюдения орбитального тела. С помощью этих двух векторов можно найти элементы орбиты и определить орбиту.

См. также

Теорема о вписанном угле и трехточечная форма эллипсов

Ссылки

^ Кертис, Ховард Д. Орбитальная механика для студентов-инженеров . Оксфорд: Эльзевир Баттерворт-Хайнеманн, 2005. Печать.
^ Гронки, Джованни Ф.. «Классическое и современное определение орбиты астероидов». Труды Международного астрономического союза 2004.IAUC196 (2004): 1-11. Распечатать.

Дер, Гим Дж. «Новые алгоритмы определения начальных орбит только для углов». Конференция по передовым технологиям оптического и космического наблюдения Мауи. (2012). Распечатать.

[1] Кертис, Ховард Д. Орбитальная механика для студентов-инженеров . Оксфорд: Эльзевир Баттерворт-Хайнеманн, 2005. Печать.

[2] Гронки, Джованни Ф.. «Классическое и современное определение орбиты астероидов». Труды Международного астрономического союза 2004.IAUC196 (2004): 1-11. Распечатать.

[ 1 ]

[ 2 ]