Точечная частица

Точечная частица , идеальная частица [1] или точечная частица (часто пишется как точечная частица ) — это идеализация частиц, широко используемых в физике . Его определяющей особенностью является отсутствие пространственного расширения ; будучи безразмерным, он не занимает места . [2] Точечная частица является подходящим представлением любого объекта, если ее размер, форма и структура не имеют значения в данном контексте. Например, с достаточно большого расстояния любой объект конечного размера будет выглядеть и вести себя как точечный объект. Точечные массы и точечные заряды, обсуждаемые ниже, являются двумя распространенными случаями. Когда точечная частица обладает аддитивным свойством, например массой или зарядом, ее часто математически представляют с помощью дельта-функции Дирака . В классической механике обычно не существует понятия вращения точечных частиц вокруг своего «центра».
В квантовой механике понятие точечной частицы осложняется принципом неопределенности Гейзенберга , поскольку даже элементарная частица , не имеющая внутренней структуры, занимает ненулевой объём. Например, атомная орбита электрона занимает в атоме водорода объём ~ 10 −30 м 3 . Тем не менее, существует различие между элементарными частицами, такими как электроны или кварки , которые не имеют известной внутренней структуры, и составными частицами, такими как протоны , которые имеют внутреннюю структуру: протон состоит из трех кварков.Элементарные частицы иногда называют «точечными частицами» из-за отсутствия у них внутренней структуры, но это в ином смысле, чем обсуждалось выше.
Точечная масса
[ редактировать ]Точечная масса ( точечная масса ) — это концепция, например, в классической физике , физического объекта (обычно материи ), который имеет ненулевую массу, но при этом явно и конкретно является (или мыслится или моделируется как) бесконечно малым (бесконечно малым). по объему или линейным размерам .В теории гравитации протяженные объекты могут вести себя как точечные даже в непосредственной близости от них. Например, сферические объекты, взаимодействующие в трехмерном пространстве , взаимодействия которых описываются ньютоновской гравитацией, ведут себя, пока они не касаются друг друга, так, как если бы вся их материя была сосредоточена в их центрах масс . [3] Фактически это справедливо для всех полей, описываемых законом обратных квадратов . [4] [5]
Начисление баллов
[ редактировать ]
Подобно точечным массам, в области электромагнетизма физики обсуждают точечный заряд , точечная частица с ненулевым электрическим зарядом . [6] Фундаментальным уравнением электростатики является , закон Кулона который описывает электрическую силу между двумя точечными зарядами. Другой результат, теорема Эрншоу , утверждает, что совокупность точечных зарядов не может поддерживаться в статической равновесной конфигурации исключительно за счет электростатического взаимодействия зарядов. Электрическое поле, связанное с классическим точечным зарядом, увеличивается до бесконечности по мере того, как расстояние от точечного заряда уменьшается до нуля, что предполагает, что модель больше не точна в этом пределе.
В квантовой механике
[ редактировать ]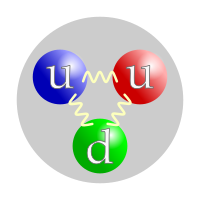
В квантовой механике существует различие между элементарной частицей (также называемой «точечной частицей») и составной частицей . Элементарная частица, такая как электрон , кварк или фотон , — это частица с неизвестной внутренней структурой. Тогда как сложная частица, например протон или нейтрон , имеет внутреннюю структуру (см. рисунок).Однако ни элементарные, ни составные частицы не локализованы в пространстве из-за принципа неопределенности Гейзенберга . частиц Волновой пакет всегда занимает ненулевой объем. Например, см. атомную орбиталь : Электрон — это элементарная частица, но его квантовые состояния образуют трехмерные структуры.
Тем не менее, есть веская причина, по которой элементарную частицу часто называют точечной. Даже если элементарная частица имеет делокализованный волновой пакет, этот волновой пакет можно представить как квантовую суперпозицию квантовых состояний , в которых частица точно локализована. Более того, взаимодействия частицы можно представить как суперпозицию взаимодействий отдельных состояний, которые локализованы. Это неверно для составной частицы, которую никогда нельзя представить как суперпозицию точно локализованных квантовых состояний. Именно в этом смысле физики могут обсуждать внутренний «размер» частицы: размер ее внутренней структуры, а не размер ее волнового пакета. «Размер» элементарной частицы в этом смысле равен нулю.
Например, для электрона экспериментальные данные показывают, что размер электрона составляет менее 10 −18 м . [7] Это соответствует ожидаемому значению, равному ровно нулю. (Это не следует путать с классическим радиусом электрона , который, несмотря на название, не связан с фактическим размером электрона.)
См. также
[ редактировать ]- Тестовая частица
- Брана
- Заряд (физика) (общее понятие, не ограничивающееся электрическим зарядом )
- Стандартная модель физики элементарных частиц
- Корпускулярно-волновой дуализм
Примечания и ссылки
[ редактировать ]Примечания
[ редактировать ]- ^ Оганян, ХК; Маркерт, Дж. Т. (2007). Физика для инженеров и ученых . Том. 1 (3-е изд.). Нортон . п. 3. ISBN 978-0-393-93003-0 .
- ^ Удвадия, FE; Калаба, RE (2007). Аналитическая динамика: новый подход . Издательство Кембриджского университета . п. 1. ISBN 978-0-521-04833-0 .
- ^ Фаулз, Грант Р.; Кэссидей, Джордж Л. Аналитическая механика . §6.2 Гравитационная сила между однородной сферой и частицей.
- ^ Ньютон, И. (1999). Принципы: математические принципы натуральной философии . Перевод Коэна, IB; Уитмен, А. Издательство Калифорнийского университета . п. 956 (предложение 75, теорема 35). ISBN 0-520-08817-4 .
- ^ И. Ньютон, А. Мотт, Дж. Мачин (1729), с. 270–271. Ньютон, И. (1729). Математические принципы натуральной философии . Перевод Мотта А.; Мачин, Дж. Бенджамин Мотт . стр. 270–271 .
- ^ Снайдер, Р. (2001). Экскурсия по математическим методам в физических науках . Издательство Кембриджского университета . стр. 196–198. ISBN 0-521-78751-3 .
- ^ «Точность определяет магнетизм электрона» . 4 октября 2006 г.
Библиография
[ редактировать ]- К. Куигг (2009). «Частица элементарная» . Американская энциклопедия . Гролье Онлайн . Архивировано из оригинала 1 апреля 2013 г. Проверено 4 июля 2009 г.
- С. Л. Глэшоу (2009). «Кварк» . Американская энциклопедия . Гролье Онлайн . Архивировано из оригинала 1 апреля 2013 г. Проверено 4 июля 2009 г.
- М. Алонсо; Э. Дж. Финн (1968). Фундаментальная университетская физика, том III: Квантовая и статистическая физика . Аддисон-Уэсли . ISBN 0-201-00262-0 .
Дальнейшее чтение
[ редактировать ]- Корниш, FHJ (1965). «Классическая теория излучения и точечные заряды». Труды Физического общества . 86 (3): 427–442. Бибкод : 1965PPS....86..427C . дои : 10.1088/0370-1328/86/3/301 .
- Ефименко, Олег Дмитриевич (1994). «Прямой расчет электрического и магнитного полей точечного электрического заряда, движущегося с постоянной скоростью». Американский журнал физики . 62 (1): 79–85. Бибкод : 1994AmJPh..62...79J . дои : 10.1119/1.17716 .
Внешние ссылки
[ редактировать ] СМИ, связанные с точечной частицей, на Викискладе?
СМИ, связанные с точечной частицей, на Викискладе?