Волновой пакет

«Волновой поезд» перенаправляется сюда. Чтобы узнать о математической концепции, см. Периодическую бегущую волну .

Зацикленная анимация волнового пакета, распространяющегося без дисперсии: огибающая сохраняется даже при изменении фазы.

В физике волновой пакет (также известный как волновой ряд или группа волн ) представляет собой короткий всплеск локализованного волнового действия, который распространяется как единое целое, очерченный огибающей . Волновой пакет может быть проанализирован или синтезирован из потенциально бесконечного набора составляющих синусоидальных волн с разными волновыми числами , с такими фазами и амплитудами, что они конструктивно интерферируют только в небольшой области пространства и деструктивно в других местах. Любой сигнал ограниченной ширины во времени или пространстве требует множества частотных составляющих вокруг центральной частоты в пределах полосы пропускания, обратно пропорциональной этой ширине; даже функция Гаусса считается волновым пакетом, потому что ее преобразование Фурье представляет собой «пакет» волн частот, сгруппированных вокруг центральной частоты. Каждая составляющая волновая функция и, следовательно, волновой пакет являются решениями волнового уравнения . В зависимости от волнового уравнения профиль волнового пакета может оставаться постоянным (отсутствие дисперсии ) или может меняться ( дисперсия ) при распространении.

Историческая справка

Идеи, связанные с волновыми пакетами – модуляцией , несущими волнами , фазовой скоростью и групповой скоростью – датируются серединой 1800-х годов. Идея групповой скорости, отличной от фазовой скорости волны, была впервые предложена У. Р. Гамильтоном в 1839 году, а первое полное рассмотрение было сделано Рэлеем в его «Теории звука» в 1877 году.

Эрвин Шредингер представил идею волновых пакетов сразу после публикации своего знаменитого волнового уравнения . Он решил свое волновое уравнение для квантового гармонического осциллятора , ввел принцип суперпозиции и использовал его, чтобы показать, что компактное состояние может сохраняться. Хотя эта работа и привела к созданию важной концепции когерентных состояний , концепция волнового пакета не сохранилась. Через год после статьи Шредингера Вернер Гейзенберг опубликовал свою статью о принципе неопределенности , показав при этом, что результаты Шредингера применимы только к квантовым гармоническим осцилляторам , а не, например, к кулоновскому потенциалу, характерному для атомов.

В следующем, 1927 году, Чарльз Гальтон Дарвин исследовал уравнение Шредингера для несвязанного электрона в свободном пространстве, предполагая, что исходный волновой пакет имеет гауссовую форму . Дарвин показал, что в свое время $t$ позже позиция $x$ пакета, движущегося со скоростью $v$ было бы

$$x_{0}+vt\pm {\sqrt {\sigma ^{2}+(ht/2\pi \sigma m)^{2}}}$$

где $\sigma$ – неопределенность в исходном положении.

Позже, в 1927 году, Пауль Эренфест показал, что время $T$ для волнового пакета материи шириной $\Delta x$ и масса $m$ распространиться в 2 раза было ${\textstyle T\approx \Delta x{\sqrt {m/\hbar }}}$. С $\hbar$ настолько мал, что волновые пакеты масштаба макроскопических объектов, с большой шириной и массой, удваиваются только в космических масштабах времени.

Значение в квантовой механике

Квантовая механика описывает природу атомных и субатомных систем с помощью волнового уравнения Шрёдингера . Классический предел квантовой механики и многие формулировки квантового рассеяния используют волновые пакеты, образованные из различных решений этого уравнения.Профили квантовых волновых пакетов изменяются по мере распространения; они показывают дисперсию. Физики пришли к выводу, что «волновые пакеты не подходят для представления субатомных частиц».

Волновые пакеты и классический предел

Шредингер разработал волновые пакеты в надежде интерпретировать квантово-волновые решения как локально компактные волновые группы. Такие пакеты обеспечивают компромисс между локализацией позиции и распространением импульса. В координатном представлении волны (например, в декартовой системе координат ) положение локализованной вероятности частицы задается положением пакетного решения. Чем уже пространственный волновой пакет и, следовательно, чем лучше локализовано положение волнового пакета, тем больше разброс импульса волны . Этот компромисс между спредом позиции и спредом импульса является характерной чертой принципа неопределенности Гейзенберга.

Один из видов оптимального компромисса минимизирует продукт неопределенности позиции. $\Delta x$ и неопределенность импульса $\Delta p_{x}$. Если мы поместим такой пакет в покое, он останется в покое: среднее значение положения и импульса соответствует классической частице. Однако он распространяется во всех направлениях со скоростью, определяемой неопределенностью оптимального количества движения. $\Delta p_{x}$. Распространение происходит настолько быстро, что на расстоянии одного круга вокруг атома волновой пакет становится неузнаваемым.

Волновые пакеты и квантовое рассеяние

называется рассеянием Взаимодействие частиц в физике ; Математика волновых пакетов играет важную роль в подходах к квантовому рассеянию . Монохроматический (одиночный импульс) источник создает трудности сходимости в моделях рассеяния. Проблемы рассеяния также имеют классические пределы. Всякий раз, когда мишень рассеяния (например, атом) имеет размер, намного меньший, чем волновой пакет, центр волнового пакета следует классическим траекториям рассеяния. В других случаях волновой пакет искажается и рассеивается при взаимодействии с целью.

Основные модели поведения

См. Также: Дисперсия (волны на воде) и Дисперсия (оптика).

Недисперсионный

Волновой пакет без дисперсии (действительная или мнимая часть)

Без дисперсии волновой пакет сохраняет свою форму по мере распространения.В качестве примера распространения без дисперсии рассмотрим волновые решения следующего волнового уравнения из классической физики: $${\partial ^{2}u \over \partial t^{2}}=c^{2}\,\nabla ^{2}u,$$

где c — скорость распространения волны в данной среде.

Используя физическое соглашение о времени, e ^{− iωt} , волновое уравнение имеет плосковолновые решения $$u(\mathbf {x} ,t)=e^{i{(\mathbf {k\cdot x} }-\omega t)},$$

где $$\omega ^{2}=|\mathbf {k} |^{2}c^{2},$$ и $|\mathbf {k} |^{2}=k_{x}^{2}+k_{y}^{2}+k_{z}^{2}.$

Это соотношение между ω и k должно быть справедливым, чтобы плоская волна была решением волнового уравнения. Оно называется дисперсионным соотношением .

Для упрощения рассмотрим только волны, распространяющиеся в одном измерении (распространение на три измерения не вызывает затруднений). Тогда общее решение $$u(x,t)=Ae^{i(kx-\omega t)}+Be^{-i(kx+\omega t)},$$в котором мы можем взять ω = kc . Первый член представляет собой волну, распространяющуюся в положительном x, направлении поскольку он является функцией x − ct только ; второй член, являющийся функцией x + ct , представляет собой волну, распространяющуюся в отрицательном x направлении .

Волновой пакет — это локализованное возмущение, возникающее в результате суммы множества различных волновых форм . Если пакет сильно локализован, необходимо больше частот, чтобы обеспечить конструктивную суперпозицию в области локализации и деструктивную суперпозицию за ее пределами. Из основных решений в одном измерении общую форму волнового пакета можно выразить как $$u(x,t)={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{\,\infty }A(k)~e^{i(kx-\omega (k)t)}\,dk.$$

Как и в случае плоской волны, волновой пакет движется вправо при ω ( k ) = kc , поскольку u ( x , t ) = F ( x − ct ) , и влево при ω ( k ) = − kc , поскольку ты ( Икс , т ) знак равно F ( Икс + ct ) .

Фактор $1/{\sqrt {2\pi }}$ происходит из соглашений о преобразовании Фурье . Амплитуда A ( k ) содержит коэффициенты линейной суперпозиции плосковолновых решений. Эти коэффициенты, в свою очередь, могут быть выражены как функция u ( x , t ), оцененная при t = 0 путем инвертирования приведенного выше соотношения преобразования Фурье: $$A(k)={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{\,\infty }u(x,0)~e^{-ikx}\,dx.$$

Например, выбирая $$u(x,0)=e^{-x^{2}+ik_{0}x},$$

мы получаем $$A(k)={\frac {1}{\sqrt {2}}}e^{-{\frac {(k-k_{0})^{2}}{4}}},$$

и наконец $${\begin{aligned}u(x,t)&=e^{-(x-ct)^{2}+ik_{0}(x-ct)}\\&=e^{-(x-ct)^{2}}\left[\cos \left(2\pi {\frac {x-ct}{\lambda }}\right)+i\sin \left(2\pi {\frac {x-ct}{\lambda }}\right)\right].\end{aligned}}$$

Недисперсионное распространение действительной или мнимой части этого волнового пакета представлено на анимации выше.

Дисперсионный

Волновой пакет с дисперсией. Обратите внимание, что волна распространяется, а ее амплитуда уменьшается.

Плотность вероятности в позиционном пространстве изначально гауссовского состояния, движущегося в одном измерении с минимально неопределенным постоянным импульсом в свободном пространстве.

Напротив, в качестве примера дисперсии , когда волна меняет форму во время распространения, вместо этого рассмотрим решения уравнения Шредингера (обезразмеренного с 2Δ x , m и ħ , установленными равными единице), $$i{\partial \psi \over \partial t}=-{\frac {1}{2}}{\nabla ^{2}\psi },$$что дает дисперсионное соотношение $$\omega ={\frac {1}{2}}|\mathbf {k} |^{2}.$$

Еще раз, ограничивая внимание одним измерением, решение уравнения Шредингера, удовлетворяющее начальному условию ${\textstyle \psi (x,0)={\sqrt[{4}]{2/\pi }}\exp \left({-x^{2}+ik_{0}x}\right)}$, представляющий волновой пакет, локализованный в пространстве в начале координат, видится как $${\begin{aligned}\psi (x,t)&={\frac {\sqrt[{4}]{2/\pi }}{\sqrt {1+2it}}}e^{-{\frac {1}{4}}k_{0}^{2}}~e^{-{\frac {1}{1+2it}}\left(x-{\frac {ik_{0}}{2}}\right)^{2}}\\&={\frac {\sqrt[{4}]{2/\pi }}{\sqrt {1+2it}}}e^{-{\frac {1}{1+4t^{2}}}(x-k_{0}t)^{2}}~e^{i{\frac {1}{1+4t^{2}}}\left((k_{0}+2tx)x-{\frac {1}{2}}tk_{0}^{2}\right)}~.\end{aligned}}$$

Впечатление о дисперсионном поведении этого волнового пакета можно получить, взглянув на плотность вероятности: $$|\psi (x,t)|^{2}={\frac {\sqrt {2/\pi }}{\sqrt {1+4t^{2}}}}~e^{-{\frac {2(x-k_{0}t)^{2}}{1+4t^{2}}}}~.$$Очевидно, что этот дисперсионный волновой пакет, двигаясь с постоянной групповой скоростью k _o , быстро делокализуется: его ширина увеличивается со временем как √ 1 + 4 t ² → 2 t , поэтому в конечном итоге он распространяется в неограниченную область пространства.

Профиль импульса A ( k ) остается инвариантным. Вероятностный ток ​ $$j=\rho v={\frac {1}{2i}}(\psi ^{*}\nabla \psi -\psi \nabla \psi ^{*})=\rho \left(k_{0}+{\frac {4t(x-k_{0}t)}{1+4t^{2}}}\right).$$

Гауссовы волновые пакеты в квантовой механике

Суперпозиция одномерных плоских волн (синий), которые в сумме образуют гауссовский волновой пакет (красный), который распространяется вправо при распространении. Синие точки соответствуют фазовой скорости каждой плоской волны, а красная линия соответствует скорости центральной группы.

Одномерный гауссов волновой пакет, показанный в комплексной плоскости, для a =2 и k =4

Вышеупомянутый дисперсионный гауссовский волновой пакет, ненормированный и просто центрированный в начале координат, вместо этого, при t = 0, теперь может быть записан в 3D, теперь в стандартных единицах: $$\psi (\mathbf {r} ,0)=e^{-\mathbf {r} \cdot \mathbf {r} /2a},$$где а — положительное действительное число, квадрат ширины волнового пакета , $$a=2\langle \mathbf {r} \cdot \mathbf {r} \rangle /3\langle 1\rangle =2(\Delta x)^{2}.$$

Преобразование Фурье также является гауссовым с точки зрения волнового числа:k -вектор ( с обратной шириной, $$1/a=2\langle \mathbf {k} \cdot \mathbf {k} \rangle /3\langle 1\rangle =2(\Delta p_{x}/\hbar )^{2},$$так что $$\Delta x\Delta p_{x}=\hbar /2,$$т. е. оно удовлетворяет соотношению неопределенности ), $$\psi (\mathbf {k} ,0)=(2\pi a)^{3/2}e^{-a\mathbf {k} \cdot \mathbf {k} /2}.$$

Каждая отдельная волна вращается во времени только по фазе, так что зависящее от времени решение с преобразованием Фурье имеет вид

${\begin{aligned}\Psi (\mathbf {k} ,t)&=(2\pi a)^{3/2}e^{-a\mathbf {k} \cdot \mathbf {k} /2}e^{-iEt/\hbar }\\&=(2\pi a)^{3/2}e^{-a\mathbf {k} \cdot \mathbf {k} /2-i(\hbar ^{2}\mathbf {k} \cdot \mathbf {k} /2m)t/\hbar }\\&=(2\pi a)^{3/2}e^{-(a+i\hbar t/m)\mathbf {k} \cdot \mathbf {k} /2}.\end{aligned}}$

Обратное преобразование Фурье по-прежнему является гауссовым, но теперь параметр a стал комплексным, и появился общий коэффициент нормализации.

$\Psi (\mathbf {r} ,t)=\left({a \over a+i\hbar t/m}\right)^{3/2}e^{-{\mathbf {r} \cdot \mathbf {r} \over 2(a+i\hbar t/m)}}.$

Интеграл от Ψ по всему пространству инвариантен, поскольку он является скалярным произведением Ψ с состоянием нулевой энергии, которое представляет собой волну с бесконечной длиной волны, постоянную функцию пространства. Для любого собственного состояния энергии η ( x ) внутренний продукт $$\langle \eta |\psi \rangle =\int \eta (\mathbf {r} )\psi (\mathbf {r} )d^{3}\mathbf {r} ,$$меняется во времени лишь простым образом: его фаза вращается с частотой, определяемой энергией η . Когда η имеет нулевую энергию, как волна с бесконечной длиной волны, она вообще не меняется.

Интеграл ∫ |Ψ| ² д ³ r также инвариантен, что является утверждением сохранения вероятности. Явно,

$P(r)=|\Psi |^{2}=\Psi ^{*}\Psi =\left({a \over {\sqrt {a^{2}+(\hbar t/m)^{2}}}}\right)^{3}~e^{-{a\,\mathbf {r} \cdot \mathbf {r} \over a^{2}+(\hbar t/m)^{2}}},$

в котором √ a — ширина P ( r ) в момент t = 0 ; r — расстояние от начала координат; скорость частицы равна нулю; и начало времени t = 0 может быть выбрано произвольно.

Ширина гауссианы — интересная величина, которую можно определить по плотности вероятности |Ψ| ² ,

$${\sqrt {a^{2}+(\hbar t/m)^{2} \over a}}.$$Эта ширина в конечном итоге растет линейно во времени, как ħt /( m √ a ) , что указывает на распространение волнового пакета .

Например, если электронный волновой пакет изначально локализован в области атомных размеров (т. е. 10 ⁻¹⁰ м) то ширина пакета увеличивается примерно в 10 раз. ⁻¹⁶ с. Очевидно, что волновые пакеты частиц действительно распространяются очень быстро (в свободном пространстве): Например, через 1 мс ширина вырастет примерно до километра.

Этот линейный рост является отражением (независимой от времени) неопределенности импульса: волновой пакет ограничен узким диапазоном Δ x = √ a /2 и, таким образом, имеет импульс, который неопределенен (согласно принципу неопределенности) на величину ħ / √ 2 a , разброс по скорости ħ/m √ 2 a , и, таким образом, в будущем положении на ħt /m √ 2 a . Тогда соотношение неопределенности представляет собой строгое неравенство, действительно очень далекое от насыщения! Первоначальная неопределенность Δ x Δ p = ħ /2 раз теперь увеличилась в ħt/ma (при больших t ).

2D

Двумерный гауссов квантовый волновой пакет. Цвет (желтый, зеленый, синий) указывает на фазу волновой функции. $\psi$, его яркость указывает $|\psi |^{2}/|\psi |_{max}^{2}$. $k_{0x}=k_{0}$, $k_{0y}=0$

Гауссова двумерная квантовая волновая функция:

$\psi (x,y,t)=\psi (x,t)\psi (y,t)$

$\psi (x,t)=({\frac {2a^{2}}{\pi }})^{1/4}{\frac {e^{i\phi }}{(a^{4}+{\frac {4\hbar ^{2}t^{2}}{m^{2}}})^{1/4}}}e^{ik_{0}x}\exp[-{\frac {(x-{\frac {\hbar k_{0}}{m}}t)^{2}}{a^{2}+{\frac {2i\hbar t}{m}}}}]$

где

$\phi =-\theta -{\frac {\hbar k_{0}^{2}}{2m}}t$

$tg(2\theta )={\frac {2\hbar t}{ma^{2}}}$

Волновой поезд Эйри

В отличие от вышеупомянутого гауссовского волнового пакета, наблюдалось что определенная волновая функция, основанная на функциях Эйри , распространяется свободно без дисперсии огибающей, сохраняя свою форму. Он ускоряется неискаженно в отсутствие силового поля: $$\psi =\operatorname {Ai} (B(x-B^{3}t^{2}))\,e^{iB^{3}t\left(x-{\tfrac {2}{3}}B^{3}t^{2}\right)}\,.$$(Для простоты ħ = 1 , m = 1/2 , а B — константа, см. обезразмеривание .)

Усеченное представление о развитии времени фронта Эйри в фазовом пространстве. (Нажмите, чтобы анимировать.)

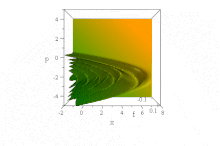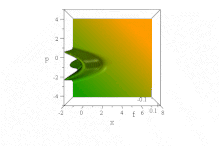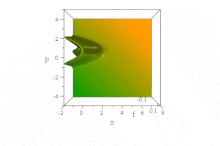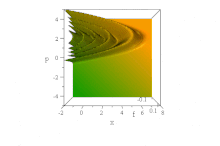
Тем не менее, в этой бессиловой ситуации нет диссонанса с теоремой Эренфеста , поскольку состояние одновременно ненормируемо и имеет неопределенное (бесконечное) ⟨ x ⟩ для всех времен. (Насколько это можно было определить, ⟨ p ⟩ = 0 во все времена, несмотря на кажущееся ускорение фронта.)

В фазовом пространстве это очевидно в чистом квазивероятном распределении Вигнера этого волнового пакета, форма которого по x и p инвариантна с течением времени, но чьи характеристики ускоряются вправо при ускорении парабол B ( x − B ³ т ² ) + ( p / B − tB ² ) ² = 0 , $$W(x,p;t)=W(x-B^{3}t^{2},p-B^{3}t;0)={1 \over 2^{1/3}\pi B}~\mathrm {Ai} \left(2^{2/3}\left(Bx+{p^{2} \over B^{2}}-2Bpt\right)\right).$$

Обратите внимание, что распределение импульса, полученное путем интегрирования по всем x, является постоянным. Поскольку это плотность вероятности в импульсном пространстве , очевидно, что сама волновая функция не нормируема.

Бесплатный распространитель

Пределом узкой ширины обсуждаемого гауссовского волнового пакета является ядро ​​свободного пропагатора K . Для других дифференциальных уравнений это обычно называют функцией Грина, но в квантовой механике принято называть функцию Грина временным преобразованием Фурье K .

Возвращаясь для простоты к одному измерению, когда m и ħ установлены равными единице, когда a представляет собой бесконечно малую величину ε , начальное условие Гаусса, масштабированное так, чтобы ее интеграл был равен единице, $$\psi _{0}(x)={1 \over {\sqrt {2\pi \varepsilon }}}e^{-{x^{2} \over 2\varepsilon }}\,$$становится дельта-функцией , δ ( x ) , так что ее эволюция во времени, $$K_{t}(x)={1 \over {\sqrt {2\pi (it+\varepsilon )}}}e^{-x^{2} \over 2it+\varepsilon }\,$$дает пропагатор.

Заметим, что очень узкий начальный волновой пакет мгновенно становится бесконечно широким, но с фазой, которая является более быстроколебательной при больших значениях x . Это может показаться странным — решение переходит от локализации в одной точке к тому, чтобы быть «везде» во все более поздние моменты времени , но это является отражением огромной неопределенности импульса локализованной частицы, как объяснено выше.

Далее заметим, что норма волновой функции бесконечна, что тоже верно, поскольку квадрат дельта-функции точно так же расходится .

Множитель, включающий ε, представляет собой бесконечно малую величину, которая обеспечивает корректность интегралов по K. определения В пределе ε → 0 K становится чисто осциллирующим, а интегралы от K не сходятся абсолютно. В оставшейся части этого раздела он будет установлен равным нулю, но для того, чтобы все интегрирования по промежуточным состояниям были четко определены, предел ε → 0 следует принимать только после расчета конечного состояния.

Пропагатор — это амплитуда достижения точки x в момент времени t , начиная с начала координат, x = 0. Благодаря трансляционной инвариантности амплитуда достижения точки x при старте из точки y представляет собой одну и ту же функцию, только теперь преобразованную: $$K_{t}(x,y)=K_{t}(x-y)={1 \over {\sqrt {2\pi it}}}e^{i(x-y)^{2} \over 2t}\,.$$

В пределе, когда t мало, пропагатор переходит к дельта-функции $$\lim _{t\to 0}K_{t}(x-y)=\delta (x-y)~,$$но только в смысле распределений : интеграл этой величины, умноженный на произвольную дифференцируемую пробную функцию, дает значение пробной функции в нуле.

Чтобы убедиться в этом, обратите внимание, что интеграл по всему пространству K всегда равен 1: $$\int K_{t}(x)dx=1\,,$$поскольку этот интеграл является внутренним произведением K с однородной волновой функцией. Но фазовый множитель в показателе степени имеет ненулевую пространственную производную везде, кроме начала координат, и поэтому, когда время мало, во всех точках, кроме одной, происходят быстрые фазовые сокращения. Это строго верно, когда предел ε → 0 берется в самом конце.

Таким образом, ядро ​​распространения — это (будущая) эволюция дельта-функции во времени, и в некотором смысле оно непрерывно: оно переходит к исходной дельта-функции на малых временах. Если исходная волновая функция представляет собой бесконечно узкий пик в положении y , $$\psi _{0}(x)=\delta (x-y)\,,$$она становится колебательной волной, $$\psi _{t}(x)={1 \over {\sqrt {2\pi it}}}e^{i(x-y)^{2}/2t}\,.$$

Теперь, поскольку каждую функцию можно записать как взвешенную сумму таких узких пиков, $$\psi _{0}(x)=\int \psi _{0}(y)\delta (x-y)dy\,,$$эволюция во времени каждой функции ψ ₀ определяется этим ядром распространения K ,

$\psi _{t}(x)=\int \psi _{0}(y){1 \over {\sqrt {2\pi it}}}e^{i(x-y)^{2}/2t}dy\,.$

Таким образом, это формальный способ выразить фундаментальное решение или общее решение . Интерпретация этого выражения заключается в том, что амплитуда частицы, находящейся в точке x в момент времени t, равна амплитуде, с которой она стартовала в точке y , умноженной на амплитуду, которую она прошла от y до x , суммированную по всем возможным начальным точкам . Другими словами, это свертка ядра K с произвольным начальным условием ψ ₀ , $$\psi _{t}=K*\psi _{0}\,.$$

Поскольку амплитуду перемещения от x до y за время t + t ' можно рассматривать в два этапа, пропагатор подчиняется тождеству состава: $$\int K(x-y;t)K(y-z;t')dy=K(x-z;t+t')~,$$что можно интерпретировать следующим образом: амплитуда перемещения от x до z за время t + t ' представляет собой сумму амплитуды перемещения от x до y за время t , умноженную на амплитуду перемещения от y до z за время t. ', суммируемый по всем возможным промежуточным состояниям y . Это свойство произвольной квантовой системы, и разделение времени на множество сегментов позволяет выразить временную эволюцию в виде интеграла по путям .

Аналитическое продолжение диффузии

См. Также: Уравнение теплопроводности § Фундаментальные решения и Ядро теплопроводности.

Распространение волновых пакетов в квантовой механике напрямую связано с разбросом плотностей вероятности при диффузии . Для частицы, которая беспорядочно ходит , функция плотности вероятности в любой точке удовлетворяет уравнению диффузии (см. также уравнение теплопроводности ) $${\partial \over \partial t}\rho ={1 \over 2}{\partial ^{2} \over \partial x^{2}}\rho ~,$$где коэффициент 2, который можно удалить путем изменения масштаба времени или пространства, используется только для удобства.

Решением этого уравнения является расширяющаяся гауссиана, $$\rho _{t}(x)={1 \over {\sqrt {2\pi t}}}e^{-x^{2} \over 2t}~,$$и, поскольку интеграл от ρ _t постоянен, в то время как ширина становится узкой на малых временах, эта функция приближается к дельта-функции при t = 0, $$\lim _{t\to 0}\rho _{t}(x)=\delta (x)$$опять же только в смысле распределений, так что $$\lim _{t\to 0}\int _{x}f(x)\rho _{t}(x)=f(0)$$для любой гладкой пробной функции f .

Распространяющийся гауссиан является ядром распространения уравнения диффузии и подчиняется тождеству свертки : $$K_{t+t'}=K_{t}*K_{t'}\,,$$что позволяет выразить диффузию как интеграл по путям. Пропагатор — это экспонента оператора H , $$K_{t}(x)=e^{-tH}\,,$$который является бесконечно малым оператором диффузии, $$H=-{\nabla ^{2} \over 2}\,.$$

Матрица имеет два индекса, что в непрерывном пространстве делает ее функцией x и x '. В этом случае из-за трансляционной инвариантности матричный элемент K зависит только от разности позиций, и удобным злоупотреблением обозначениями является обращение к оператору, матричным элементам и функции разности под одним и тем же именем: $$K_{t}(x,x')=K_{t}(x-x')\,.$$

Трансляционная инвариантность означает, что непрерывное умножение матриц $$C(x,x'')=\int _{x'}A(x,x')B(x',x'')\,,$$по сути является сверткой, $$C(\Delta )=C(x-x'')=\int _{x'}A(x-x')B(x'-x'')=\int _{y}A(\Delta -y)B(y)\,.$$

Экспонента может быть определена в диапазоне t s, который включает комплексные значения, при условии, что интегралы по ядру распространения остаются сходящимися, $$K_{z}(x)=e^{-zH}\,.$$Пока действительная часть z положительна, для больших значений K x экспоненциально убывает, и интегралы по K действительно абсолютно сходятся.

Пределом этого выражения для z, приближающегося к чисто мнимой оси, является встреченный выше пропагатор Шрёдингера: $$K_{t}^{\rm {Schr}}=K_{it+\varepsilon }=e^{-(it+\varepsilon )H}\,,$$что иллюстрирует описанную выше временную эволюцию гауссиан.

Исходя из фундаментальной идентичности возведения в степень или интеграции путей, $$K_{z}*K_{z'}=K_{z+z'}\,$$справедливо для всех комплексных значений z , где интегралы абсолютно сходятся, так что операторы корректно определены.

Таким образом, квантовая эволюция гауссианы, которая представляет собой комплексное диффузионное ядро ​​K , $$\psi _{0}(x)=K_{a}(x)=K_{a}*\delta (x)\,$$представляет собой эволюционировавшее во времени состояние, $$\psi _{t}=K_{it}*K_{a}=K_{a+it}\,.$$

Это иллюстрирует вышеупомянутую диффузионную форму комплексных гауссовских решений: $$\psi _{t}(x)={1 \over {\sqrt {2\pi (a+it)}}}e^{-{x^{2} \over 2(a+it)}}\,.$$

См. также

• Волна
• Распространение волн
• Фурье-анализ
• Групповая скорость
• Фазовая скорость
• Свободная частица
• Когерентные состояния
• Форма волны
• Вейвлет
• Волна материи
• Импульсный (обработка сигнала)
• Пульс (физика)
• Уравнение Шрёдингера
• Введение в квантовую механику
• Солитон

Внешние ссылки

• Учебные материалы, связанные с движением волновых пакетов , в Викиверситете
• Словарное определение волнового пакета в Викисловаре
• График пакета 1d Wave в Google
• Последовательность волн 1d и график плотности вероятности в Google
• График пакетов 2d Wave в Google
• График поезда 2d Wave в Google
• 2D-график плотности вероятности в Google
• Квантовая физика онлайн: Интерактивное моделирование свободного волнового пакета
• Веб-Шрёдингер : Интерактивное 2D-моделирование динамики волновых пакетов
• Моделирование волнового пакета в 2D (По данным ФУРЬЕ-синтеза в 2D)