Параболические координаты

Параболические координаты — это двумерная ортогональная система координат , в которой координатные линии представляют собой софокусные параболы . Трехмерная версия параболических координат получается вращением двумерной системы вокруг оси симметрии парабол.

Параболические координаты нашли множество применений, например, при рассмотрении эффекта Штарка и потенциальной теории ребер.

Двумерные параболические координаты

Двумерные параболические координаты $(\sigma ,\tau )$ определяются уравнениями в декартовых координатах:

x=\sigma \tau

y={\frac {1}{2}}\left(\tau ^{2}-\sigma ^{2}\right)

Кривые постоянной $\sigma$ форма конфокальной параболы

2y={\frac {x^{2}}{\sigma ^{2}}}-\sigma ^{2}

которые открываются вверх (т.е. в сторону $+y$ ), тогда как кривые константы $\tau$ форма конфокальной параболы

2y=-{\frac {x^{2}}{\tau ^{2}}}+\tau ^{2}

которые открываются вниз (т.е. в сторону $-y$ ). Фокусы всех этих парабол расположены в начале координат.

Декартовы координаты $x$ и $y$ можно преобразовать в параболические координаты:

\sigma =\operatorname {sign} (x){\sqrt {{\sqrt {x^{2}+y^{2}}}-y}}

\tau ={\sqrt {{\sqrt {x^{2}+y^{2}}}+y}}

Двумерные масштабные коэффициенты

Масштабные коэффициенты для параболических координат $(\sigma ,\tau )$ равны

h_{\sigma }=h_{\tau }={\sqrt {\sigma ^{2}+\tau ^{2}}}

Следовательно, бесконечно малый элемент площади равен

dA=\left(\sigma ^{2}+\tau ^{2}\right)d\sigma d\tau

а лапласиан равен

\nabla ^{2}\Phi ={\frac {1}{\sigma ^{2}+\tau ^{2}}}\left({\frac {\partial ^{2}\Phi }{\partial \sigma ^{2}}}+{\frac {\partial ^{2}\Phi }{\partial \tau ^{2}}}\right)

Другие дифференциальные операторы, такие как $\nabla \cdot \mathbf {F}$ и $\nabla \times \mathbf {F}$ можно выразить в координатах $(\sigma ,\tau )$ заменив масштабные коэффициенты в общие формулы находится в ортогональных координатах .

Трехмерные параболические координаты

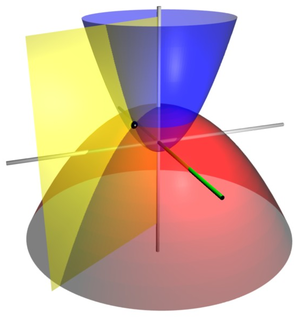
Двумерные параболические координаты образуют основу для двух наборов трехмерных ортогональных координат . Параболические цилиндрические координаты получаются путем проецирования в $z$ -направление.Вращение вокруг оси симметрии парабол создает набор конфокальные параболоиды, система координат трехмерных параболических координат. Выражается в декартовых координатах:

x=\sigma \tau \cos \varphi

y=\sigma \tau \sin \varphi

z={\frac {1}{2}}\left(\tau ^{2}-\sigma ^{2}\right)

где параболы теперь совпадают с $z$ -ось,вокруг которого осуществлялся поворот. Следовательно, азимутальный угол $\varphi$ определяется

\tan \varphi ={\frac {y}{x}}

Поверхности постоянных $\sigma$ образуют конфокальные параболоиды

2z={\frac {x^{2}+y^{2}}{\sigma ^{2}}}-\sigma ^{2}

которые открываются вверх (т.е. в сторону $+z$ ), тогда как поверхности постоянных $\tau$ образуют конфокальные параболоиды

2z=-{\frac {x^{2}+y^{2}}{\tau ^{2}}}+\tau ^{2}

которые открываются вниз (т.е. в сторону $-z$ ). Фокусы всех этих параболоидов расположены в начале координат.

Риманов связанный метрический тензор, с этой системой координат, равен

g_{ij}={\begin{bmatrix}\sigma ^{2}+\tau ^{2}&0&0\\0&\sigma ^{2}+\tau ^{2}&0\\0&0&\sigma ^{2}\tau ^{2}\end{bmatrix}}

Трехмерные масштабные коэффициенты

Трехмерные масштабные коэффициенты:

h_{\sigma }={\sqrt {\sigma ^{2}+\tau ^{2}}}

h_{\tau }={\sqrt {\sigma ^{2}+\tau ^{2}}}

h_{\varphi }=\sigma \tau

Видно, что масштабные факторы $h_{\sigma }$ и $h_{\tau }$ такие же, как и в двумерном случае. Тогда бесконечно малый элемент объема равен

dV=h_{\sigma }h_{\tau }h_{\varphi }\,d\sigma \,d\tau \,d\varphi =\sigma \tau \left(\sigma ^{2}+\tau ^{2}\right)\,d\sigma \,d\tau \,d\varphi

а лапласиан определяется выражением

\nabla ^{2}\Phi ={\frac {1}{\sigma ^{2}+\tau ^{2}}}\left[{\frac {1}{\sigma }}{\frac {\partial }{\partial \sigma }}\left(\sigma {\frac {\partial \Phi }{\partial \sigma }}\right)+{\frac {1}{\tau }}{\frac {\partial }{\partial \tau }}\left(\tau {\frac {\partial \Phi }{\partial \tau }}\right)\right]+{\frac {1}{\sigma ^{2}\tau ^{2}}}{\frac {\partial ^{2}\Phi }{\partial \varphi ^{2}}}

Другие дифференциальные операторы, такие как $\nabla \cdot \mathbf {F}$ и $\nabla \times \mathbf {F}$ можно выразить в координатах $(\sigma ,\tau ,\phi )$ заменив масштабные коэффициенты в общие формулы находится в ортогональных координатах .

См. также

Библиография

Морс П.М. , Фешбах Х. (1953). Методы теоретической физики . Часть I. Нью-Йорк: МакГроу-Хилл. п. 660. ИСБН 0-07-043316-Х . LCCN 52011515 .
Маргенау Х. , Мерфи Г.М. (1956). Математика физики и химии . Нью-Йорк: Д. ван Ностранд. стр. 185–186 . LCCN 55010911 .
Корн Г.А., Корн ТМ (1961). Математический справочник для ученых и инженеров . Нью-Йорк: МакГроу-Хилл. п. 180. LCCN 59014456 . АСИН B0000CKZX7.
Зауэр Р., Сабо I (1967). Математический инструментарий инженера . Нью-Йорк: Springer Verlag. п. 96. LCCN 67025285 .
Цвиллингер Д. (1992). Справочник по интеграции . Бостон, Массачусетс: Джонс и Бартлетт. п. 114. ИСБН 0-86720-293-9 . что и Морс и Фешбах (1953), с заменой uk _{ξ k} на _{То же ,} .
Мун П., Спенсер Д.Э. (1988). «Параболические координаты (μ, ν, ψ)». Справочник по теории поля, включая системы координат, дифференциальные уравнения и их решения (исправленное 2-е изд., 3-е печатное изд.). Нью-Йорк: Springer-Verlag. С. 34–36 (табл. 1.08). ISBN 978-0-387-18430-2 .

Внешние ссылки