Вытянутые сфероидальные координаты

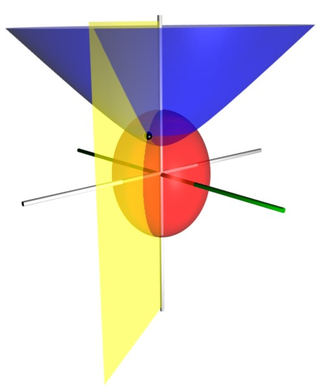
Вытянутые сфероидальные координаты представляют собой трехмерную ортогональную систему координат , возникающую в результате вращения двумерной эллиптической системы координат вокруг фокальной оси эллипса, т. е. оси симметрии, на которой расположены фокусы. Вращение вокруг другой оси дает сплющенные сфероидальные координаты . Вытянутые сфероидальные координаты также можно рассматривать как предельный случай эллипсоидальных координат, в которых две наименьшие главные оси равны по длине.

Вытянутые сфероидальные координаты можно использовать для решения различных уравнений в частных производных , в которых граничные условия соответствуют его симметрии и форме, например, для решения поля, создаваемого двумя центрами, которые считаются фокусами на оси z . Одним из примеров является решение волновой функции электрона , движущегося в электромагнитном поле двух положительно заряженных ядер , например, в молекулярном ионе водорода H _{2 .}⁺. Другой пример — расчет электрического поля, создаваемого двумя небольшими кончиками электродов . Другие предельные случаи включают области, образованные отрезком линии ( μ = 0) или линией с отсутствующим сегментом (ν=0). Электронная структура обычных двухатомных молекул со многими электронами также может быть решена с превосходной точностью в вытянутой сфероидальной системе координат. ^[1]

Определение

Вытянутые сфероидальные координаты µ и ν для a = 1. Линии равных значений µ и ν показаны на *плоскости xz* , т.е. для φ = 0. Поверхности постоянных µ и ν получаются вращением вокруг z оси . , так что диаграмма справедлива для любой плоскости, содержащей ось z : т.е. для любого φ .

Наиболее распространенное определение вытянутых сфероидальных координат. $(\mu ,\nu ,\varphi )$ является

x=a\sinh \mu \sin \nu \cos \varphi

y=a\sinh \mu \sin \nu \sin \varphi

z=a\cosh \mu \cos \nu

где $\mu$ является неотрицательным действительным числом и $\nu \in [0,\pi ]$ . Азимутальный угол $\varphi$ принадлежит интервалу $[0,2\pi ]$ .

Тригонометрическое тождество

{\frac {z^{2}}{a^{2}\cosh ^{2}\mu }}+{\frac {x^{2}+y^{2}}{a^{2}\sinh ^{2}\mu }}=\cos ^{2}\nu +\sin ^{2}\nu =1

показывает, что поверхности постоянной $\mu$ образуют вытянутые сфероиды , так как представляют собой эллипсы , повернутые вокруг оси присоединяясь к их фокусам. Аналогично, гиперболическое тригонометрическое тождество

{\frac {z^{2}}{a^{2}\cos ^{2}\nu }}-{\frac {x^{2}+y^{2}}{a^{2}\sin ^{2}\nu }}=\cosh ^{2}\mu -\sinh ^{2}\mu =1

показывает, что поверхности постоянной $\nu$ форма гиперболоиды революции.

Расстояния от очагов, расположенных в $(x,y,z)=(0,0,\pm a)$ являются

r_{\pm }={\sqrt {x^{2}+y^{2}+(z\mp a)^{2}}}=a(\cosh \mu \mp \cos \nu ).

Масштабные коэффициенты

Масштабные коэффициенты для эллиптических координат $(\mu ,\nu )$ равны

h_{\mu }=h_{\nu }=a{\sqrt {\sinh ^{2}\mu +\sin ^{2}\nu }}

тогда как азимутальный масштабный коэффициент равен

h_{\varphi }=a\sinh \mu \sin \nu ,

в результате чего получается метрика

{\begin{aligned}ds^{2}&=h_{\mu }^{2}d\mu ^{2}+h_{\nu }^{2}d\nu ^{2}+h_{\varphi }^{2}d\varphi ^{2}\\&=a^{2}\left[(\sinh ^{2}\mu +\sin ^{2}\nu )d\mu ^{2}+(\sinh ^{2}\mu +\sin ^{2}\nu )d\nu ^{2}+(\sinh ^{2}\mu \sin ^{2}\nu )d\varphi ^{2}\right].\end{aligned}}

Следовательно, бесконечно малый элемент объема равен

dV=a^{3}\sinh \mu \sin \nu (\sinh ^{2}\mu +\sin ^{2}\nu )\,d\mu \,d\nu \,d\varphi

и лапласиан можно записать

{\begin{aligned}\nabla ^{2}\Phi ={}&{\frac {1}{a^{2}(\sinh ^{2}\mu +\sin ^{2}\nu )}}\left[{\frac {\partial ^{2}\Phi }{\partial \mu ^{2}}}+{\frac {\partial ^{2}\Phi }{\partial \nu ^{2}}}+\coth \mu {\frac {\partial \Phi }{\partial \mu }}+\cot \nu {\frac {\partial \Phi }{\partial \nu }}\right]\\[6pt]&{}+{\frac {1}{a^{2}\sinh ^{2}\mu \sin ^{2}\nu }}{\frac {\partial ^{2}\Phi }{\partial \varphi ^{2}}}\end{aligned}}

Другие дифференциальные операторы, такие как $\nabla \cdot \mathbf {F}$ и $\nabla \times \mathbf {F}$ можно выразить в координатах $(\mu ,\nu ,\varphi )$ путем подстановки масштабных коэффициентов в общие формулы, найденные в ортогональных координатах .

Альтернативное определение

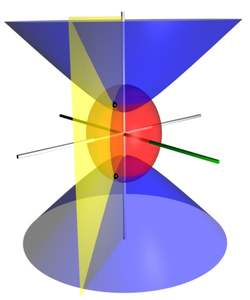
Альтернативный и геометрически интуитивно понятный набор вытянутых сфероидальных координат. $(\sigma ,\tau ,\phi )$ иногда используются, где $\sigma =\cosh \mu$ и $\tau =\cos \nu$ . Следовательно, кривые константы $\sigma$ представляют собой вытянутые сфероиды, тогда как кривые постоянной $\tau$ являются гиперболоидами революции. Координата $\tau$ принадлежит интервалу [−1, 1], тогда как $\sigma$ координата должна быть больше или равна единице.

Координаты $\sigma$ и $\tau$ имеют простую связь с расстояниями до фокусов $F_{1}$ и $F_{2}$ . Для любой точки плоскости сумма $d_{1}+d_{2}$ его расстояний до фокусов равно $2a\sigma$ , тогда как их разница $d_{1}-d_{2}$ равно $2a\tau$ . Таким образом, расстояние до $F_{1}$ является $a(\sigma +\tau )$ , тогда как расстояние до $F_{2}$ является $a(\sigma -\tau )$ . (Напомним, что $F_{1}$ и $F_{2}$ расположены в $z=-a$ и $z=+a$ соответственно.) Это дает следующие выражения для $\sigma$ , $\tau$ , и $\varphi$ :

\sigma ={\frac {1}{2a}}\left({\sqrt {x^{2}+y^{2}+(z+a)^{2}}}+{\sqrt {x^{2}+y^{2}+(z-a)^{2}}}\right)

\tau ={\frac {1}{2a}}\left({\sqrt {x^{2}+y^{2}+(z+a)^{2}}}-{\sqrt {x^{2}+y^{2}+(z-a)^{2}}}\right)

\varphi =\arctan \left({\frac {y}{x}}\right)

В отличие от аналогичных сплюснутых сфероидальных координат , вытянутые сфероидальные координаты (σ, τ, φ) не вырождены; существует уникальное обратимое соответствие. другими словами, между ними и декартовыми координатами

x=a{\sqrt {(\sigma ^{2}-1)(1-\tau ^{2})}}\cos \varphi

y=a{\sqrt {(\sigma ^{2}-1)(1-\tau ^{2})}}\sin \varphi

z=a\ \sigma \ \tau

Альтернативные масштабные коэффициенты

Масштабные коэффициенты для альтернативных эллиптических координат $(\sigma ,\tau ,\varphi )$ являются

h_{\sigma }=a{\sqrt {\frac {\sigma ^{2}-\tau ^{2}}{\sigma ^{2}-1}}}

h_{\tau }=a{\sqrt {\frac {\sigma ^{2}-\tau ^{2}}{1-\tau ^{2}}}}

в то время как азимутальный масштабный коэффициент теперь равен

h_{\varphi }=a{\sqrt {\left(\sigma ^{2}-1\right)\left(1-\tau ^{2}\right)}}

Следовательно, бесконечно малый элемент объема становится

dV=a^{3}(\sigma ^{2}-\tau ^{2})\,d\sigma \,d\tau \,d\varphi

а лапласиан равен

{\begin{aligned}\nabla ^{2}\Phi ={}&{\frac {1}{a^{2}(\sigma ^{2}-\tau ^{2})}}\left\{{\frac {\partial }{\partial \sigma }}\left[\left(\sigma ^{2}-1\right){\frac {\partial \Phi }{\partial \sigma }}\right]+{\frac {\partial }{\partial \tau }}\left[(1-\tau ^{2}){\frac {\partial \Phi }{\partial \tau }}\right]\right\}\\&{}+{\frac {1}{a^{2}(\sigma ^{2}-1)(1-\tau ^{2})}}{\frac {\partial ^{2}\Phi }{\partial \varphi ^{2}}}\end{aligned}}

Другие дифференциальные операторы, такие как $\nabla \cdot \mathbf {F}$ и $\nabla \times \mathbf {F}$ можно выразить в координатах $(\sigma ,\tau )$ путем подстановки масштабных коэффициентов в общие формулы, найденные в ортогональных координатах .

Как и в случае со сферическими координатами , уравнение Лапласа может быть решено методом разделения переменных с получением решений в виде вытянутых сфероидальных гармоник , которые удобно использовать при задании граничных условий на поверхности с постоянной вытянутой сфероидальной координатой. (См. Смайт, 1968).

Ссылки

^ Лехтола, Суси (21 мая 2019 г.). «Обзор нерелятивистских, полностью численных расчетов электронной структуры атомов и двухатомных молекул» . Межд. Дж. Квантум Хим . 119 : e25968. arXiv : 1902.01431 . дои : 10.1002/qua.25968 .

Библиография

Никаких соглашений об углах

Морс ПМ, Фешбах Х (1953). Методы теоретической физики . Часть I. Нью-Йорк: МакГроу-Хилл. п. 661. Использует ξ ₁ = a ch µ , ξ ₂ = sin ν и ξ ₃ = cos φ .
Цвиллингер Д. (1992). Справочник по интеграции . Бостон, Массачусетс: Джонс и Бартлетт. п. 114. ИСБН 0-86720-293-9 . что и Морс и Фешбах (1953), с заменой uk _k на ξ _{То же ,} .
Смайт, WR (1968). Статическое и динамическое электричество (3-е изд.). Нью-Йорк: МакГроу-Хилл.
Зауэр Р., Сабо I (1967). Математический инструментарий инженера . Нью-Йорк: Springer Verlag. п. 97. LCCN 67025285 . Использует координаты ξ = ch µ , η = sin ν и φ .

Угловое соглашение

Корн Г.А., Корн ТМ (1961). Математический справочник для ученых и инженеров . Нью-Йорк: МакГроу-Хилл. п. 177 . LCCN 59014456 . Корн и Корн используют координаты (μ, ν, φ), но также вводят вырожденные координаты (σ, τ, φ).
Маргенау Х., Мерфи GM (1956). Математика физики и химии . Нью-Йорк: Д. ван Ностранд. стр. 180–182 . LCCN 55010911 . Аналогично Корну и Корну (1961), но использует широту θ = 90 ° - ν вместо широты ν.
Мун П.Х., Спенсер Д.Э. (1988). «Вытянутые сфероидальные координаты (η, θ, ψ)». Справочник по теории поля, включая системы координат, дифференциальные уравнения и их решения (исправленное 2-е изд., 3-е печатное изд.). Нью-Йорк: Springer Verlag. С. 28–30 (табл. 1.06). ISBN 0-387-02732-7 . Мун и Спенсер используют соглашение о широте θ = 90° − ν и переименовывают φ в ψ .

Необычная конвенция

Ландау Л.Д., Лифшиц Е.М., Питаевский Л.П. (1984). Электродинамика сплошных сред (Том 8 курса теоретической физики ) (2-е изд.). Нью-Йорк: Пергамон Пресс. стр. 19–29. ISBN 978-0-7506-2634-7 . Рассматривает вытянутые сфероидальные координаты как предельный случай общих эллипсоидальных координат . Использует координаты (ξ, η, ζ), в которых единицы измерения квадрата расстояния.

Внешние ссылки

Описание MathWorld вытянутых сфероидальных координат

[diatomicreview-1] Лехтола, Суси (21 мая 2019 г.). «Обзор нерелятивистских, полностью численных расчетов электронной структуры атомов и двухатомных молекул» . Межд. Дж. Квантум Хим . 119 : e25968. arXiv : 1902.01431 . дои : 10.1002/qua.25968 .

[1]