Биполярные координаты

Биполярные координаты — это двумерная ортогональная система координат, основанная на аполлонических кругах . ^[1] Как ни странно, тот же термин иногда используется для двухцентровых биполярных координат . Существует также третья система, основанная на двух полюсах ( двуугольные координаты ).

Термин «биполярный» далее иногда используется для описания других кривых, имеющих две особые точки (фокусы), таких как эллипсы , гиперболы и овалы Кассини . Однако термин «биполярные координаты» зарезервирован для координат, описанных здесь, и никогда не используется для систем, связанных с этими другими кривыми, таких как эллиптические координаты .

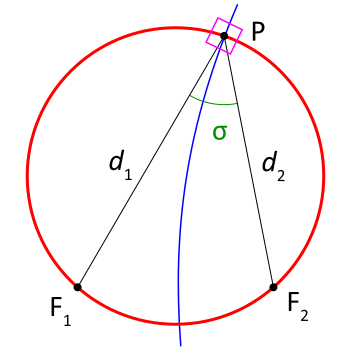
Определение

В основе системы лежат два фокуса F ₁ и F ₂ . Обращаясь к рисунку справа, σ -координата точки P равна углу F ₁ P F ₂ , а τ -координата равна натуральному логарифму отношения расстояний d ₁ и d ₂ :

\tau =\ln {\frac {d_{1}}{d_{2}}}.

Если в декартовой системе фокусы лежат в точках (− a , 0) и ( a , 0), то координаты точки P равны

x=a\ {\frac {\sinh \tau }{\cosh \tau -\cos \sigma }},\qquad y=a\ {\frac {\sin \sigma }{\cosh \tau -\cos \sigma }}.

Координата τ находится в пределах $-\infty$ (для точек, близких к F ₁ ) до $\infty$ (для точек, близких к F ₂ ). Координата σ определяется только по модулю 2π , и ее лучше всего принимать в диапазоне от -π до π , принимая ее за отрицательное значение острого угла F ₁ P F _2, если P находится в нижней полуплоскости.

Доказательство того, что система координат ортогональна.

Уравнения для x и y можно объединить, чтобы получить

x+iy=ai\cot \left({\frac {\sigma +i\tau }{2}}\right)

^[2]^[3]

или

x+iy=a\coth \left({\frac {\tau -i\sigma }{2}}\right).

Это уравнение показывает, что σ и τ — действительная и мнимая части аналитической функции от x+iy (с логарифмическими точками ветвления в фокусах), что, в свою очередь, доказывает (путем обращения к общей теории отображения ) конформного уравнения Римана ), что именно эти кривые σ и τ пересекаются под прямым углом, т. е. это ортогональная система координат .

Кривые постоянных σ и τ

Кривые постоянной σ соответствуют неконцентрическим окружностям

x^{2}+\left(y-a\cot \sigma \right)^{2}={\frac {a^{2}}{\sin ^{2}\sigma }}=a^{2}(1+\cot ^{2}\sigma )

(1)

которые пересекаются в двух фокусах. Центры кругов постоянной σ лежат на оси y в точке $a\cot \sigma$ с радиусом ${\tfrac {a}{\sin \sigma }}$ . Круги с положительным σ расположены над осью x , тогда как круги с отрицательным σ лежат под осью. Как величина | σ |- π /2 уменьшается, радиус окружностей уменьшается и центр приближается к началу координат (0, 0), что достигается при | σ | = π /2. (Из элементарной геометрии все треугольники окружности с двумя вершинами на противоположных концах диаметра являются прямоугольными.)

Кривые постоянной $\tau$ это непересекающиеся круги разных радиусов

\left(x-a\coth \tau \right)^{2}+y^{2}={\frac {a^{2}}{\sinh ^{2}\tau }}=a^{2}(\coth ^{2}\tau -1)

(2)

которые окружают фокусы, но опять-таки не концентричны. Центры кругов постоянной τ лежат на оси x в точке $a\coth \tau$ с радиусом ${\tfrac {a}{\sinh \tau }}$ . Окружности с положительным τ лежат в правой части плоскости ( x > 0), тогда как окружности с отрицательным τ лежат в левой части плоскости ( x < 0). Кривая τ = = 0 соответствует оси y ( x 0). С увеличением величины τ радиус кругов уменьшается и их центры приближаются к фокусам.

Обратные отношения

Переход от декартовых координат к биполярным координатам можно осуществить по следующим формулам:

\tau ={\frac {1}{2}}\ln {\frac {(x+a)^{2}+y^{2}}{(x-a)^{2}+y^{2}}}

и

\pi -\sigma =2\arctan {\frac {2ay}{a^{2}-x^{2}-y^{2}+{\sqrt {(a^{2}-x^{2}-y^{2})^{2}+4a^{2}y^{2}}}}}.

Координаты также имеют тождества:

\tanh \tau ={\frac {2ax}{x^{2}+y^{2}+a^{2}}}

и

\tan \sigma ={\frac {2ay}{x^{2}+y^{2}-a^{2}}},

который можно получить, решив уравнение. (1) и (2) для $\cot \sigma$ и $\coth \tau$ , соответственно.

Масштабные коэффициенты

Для получения масштабных коэффициентов для биполярных координат возьмем дифференциал уравнения для $x+iy$ , что дает

dx+i\,dy={\frac {-ia}{\sin ^{2}{\bigl (}{\tfrac {1}{2}}(\sigma +i\tau ){\bigr )}}}(d\sigma +i\,d\tau ).

Умножение этого уравнения на его комплексно-сопряженное уравнение дает

(dx)^{2}+(dy)^{2}={\frac {a^{2}}{{\bigl [}2\sin {\tfrac {1}{2}}{\bigl (}\sigma +i\tau {\bigr )}\sin {\tfrac {1}{2}}{\bigl (}\sigma -i\tau {\bigr )}{\bigr ]}^{2}}}{\bigl (}(d\sigma )^{2}+(d\tau )^{2}{\bigr )}.

Используя тригонометрические тождества для произведений синусов и косинусов, получаем

2\sin {\tfrac {1}{2}}{\bigl (}\sigma +i\tau {\bigr )}\sin {\tfrac {1}{2}}{\bigl (}\sigma -i\tau {\bigr )}=\cos \sigma -\cosh \tau ,

из чего следует, что

(dx)^{2}+(dy)^{2}={\frac {a^{2}}{(\cosh \tau -\cos \sigma )^{2}}}{\bigl (}(d\sigma )^{2}+(d\tau )^{2}{\bigr )}.

Следовательно, масштабные коэффициенты для σ и τ равны и определяются выражением

h_{\sigma }=h_{\tau }={\frac {a}{\cosh \tau -\cos \sigma }}.

Многие результаты теперь быстро вытекают из общих формул для ортогональных координат .Таким образом, бесконечно малый элемент площади равен

dA={\frac {a^{2}}{\left(\cosh \tau -\cos \sigma \right)^{2}}}\,d\sigma \,d\tau ,

а лапласиан определяется выражением

\nabla ^{2}\Phi ={\frac {1}{a^{2}}}\left(\cosh \tau -\cos \sigma \right)^{2}\left({\frac {\partial ^{2}\Phi }{\partial \sigma ^{2}}}+{\frac {\partial ^{2}\Phi }{\partial \tau ^{2}}}\right).

Выражения для $\nabla f$ , $\nabla \cdot \mathbf {F}$ , и $\nabla \times \mathbf {F}$ можно выразить полученными подстановкой масштабных коэффициентов в общие формулы, найденные в ортогональных координатах .

Приложения

Классические применения биполярных координат заключаются в решении уравнений в частных производных , например, уравнения Лапласа или уравнения Гельмгольца , для которых биполярные координаты допускают разделение переменных . Примером может служить электрическое поле, окружающее два параллельных цилиндрических проводника неравных диаметров.

Расширение до 3-х измерений

Биполярные координаты составляют основу нескольких наборов трехмерных ортогональных координат .

Биполярные цилиндрические координаты получаются путем перемещения биполярных координат вдоль оси z , т.е. оси вне плоскости.

Бисферические координаты получаются путем вращения биполярных координат вокруг оси x , т.е. оси, соединяющей фокусы.

Тороидальные координаты получаются путем вращения биполярных координат вокруг оси y , т.е. оси, разделяющей фокусы.

См. также

Эллиптическая система координат

Внешние ссылки

Интерактивная демоверсия с Desmos https://www.desmos.com/calculator/nbvnucu4o5

Ссылки

^ Эрик В. Вайсштейн, Компакт-диск «Краткая энциклопедия математики» , Биполярные координаты , компакт-диск, издание 1.0, 20 мая 1999 г. «Биполярные координаты» . Архивировано из оригинала 12 декабря 2007 года . Проверено 9 декабря 2006 г.
^ Полянин, Андрей Дмитриевич (2002). Справочник по линейным уравнениям в частных производных для инженеров и ученых . ЦРК Пресс. п. 476. ИСБН 1-58488-299-9 .
^ Хаппель, Джон; Бреннер, Ховард (1983). Гидродинамика с низким числом Рейнольдса: со специальными приложениями к дисперсным средам . Механика жидкостей и процессы транспорта. Том. 1. Спрингер. п. 497. ИСБН 978-90-247-2877-0 .

«Биполярные координаты» , Математическая энциклопедия , EMS Press , 2001 [1994]
Корн ГА и Корн ТМ . (1961) Математический справочник для ученых и инженеров , МакГроу-Хилл.

[bip-1] Эрик В. Вайсштейн, Компакт-диск «Краткая энциклопедия математики» , Биполярные координаты , компакт-диск, издание 1.0, 20 мая 1999 г. «Биполярные координаты» . Архивировано из оригинала 12 декабря 2007 года . Проверено 9 декабря 2006 г.

[Polyanin-2] Полянин, Андрей Дмитриевич (2002). Справочник по линейным уравнениям в частных производных для инженеров и ученых . ЦРК Пресс. п. 476. ИСБН 1-58488-299-9 .

[Happel-3] Хаппель, Джон; Бреннер, Ховард (1983). Гидродинамика с низким числом Рейнольдса: со специальными приложениями к дисперсным средам . Механика жидкостей и процессы транспорта. Том. 1. Спрингер. п. 497. ИСБН 978-90-247-2877-0 .

[1]

[2]

[3]