Квадрисеканс

В геометрии квадратиссекающая линия или квадратиссекающая линия пространственной кривой — это , проходящая через четыре точки кривой. Это максимально возможное количество пересечений, которое общая пространственная кривая может иметь с линией, и для таких кривых квадратисексанты образуют дискретный набор линий. Квадрисекансы изучались для кривых нескольких типов:

Узлы и звенья в теории узлов , когда они нетривиальны , всегда имеют квадрисекансы, а существование и количество квадрисекансов изучалось в связи с инвариантами узла, включая минимальную полную кривизну и длину веревки узла.
Число квадрисекансов неособой алгебраической кривой в комплексном проективном пространстве можно вычислить по формуле, выведенной Артуром Кэли .
Квадрисеканты расположения косых линий касаются подмножества четырех линий из расположения. Они связаны с линейчатыми поверхностями и конфигурацией двойной шестерки Шлефли .

Определение и мотивация

Квадрисеканс — это линия, пересекающая кривую, поверхность или другой набор в четырех различных точках. Это аналог секущей линии , линии, пересекающей кривую или поверхность в двух точках; и трисеканс — линия, пересекающая кривую или поверхность в трёх точках. ^[2]

По сравнению с секущими и трисекансами, квадрисекансы особенно актуальны для пространственных кривых , поскольку они имеют максимально возможное количество точек пересечения прямой с общей кривой . На плоскости общую кривую можно пересекать линией сколь угодно много раз; например, небольшие общие возмущения синусоидальной кривой бесконечно часто пересекаются горизонтальной осью. Напротив, если произвольная пространственная кривая возмущена на небольшое расстояние, чтобы сделать ее общей, не будет линий, проходящих через пять или более точек возмущенной кривой. Тем не менее, любые квадратисексанты исходной пространственной кривой останутся поблизости в ее возмущении. ^[3] Для общих пространственных кривых квадрисеканты образуют дискретный набор прямых. Напротив, когда встречаются трисекансы, они образуют непрерывные семейства линий. ^[4]

Одно из объяснений этого явления визуальное: глядя на кривую пространства издалека, пространство таких точек зрения можно описать как двумерную сферу, где каждому направлению соответствует одна точка. Пары нитей кривой могут казаться пересекающимися со всех этих точек зрения или с их двумерного подмножества. Три нити образуют тройное пересечение, когда точка зрения лежит на трисекансе, а четыре нити образуют четверное пересечение с точки зрения на квадрисеканс. Каждое ограничение, заключающееся в том, что пересечение пары нитей лежит на другой нити, уменьшает количество степеней свободы на одну (для общей кривой), поэтому точки зрения на трисекансы образуют одномерное (непрерывно бесконечное) подмножество сферы. , а точки зрения на квадрисекансы образуют нульмерное (дискретное) подмножество. CTC Wall пишет, что тот факт, что общие пространственные кривые пересекаются прямыми не более четырех раз, является «одной из простейших теорем такого рода», модельным случаем для аналогичных теорем о трансверсалях более высоких размерностей. ^[3]

В зависимости от свойств кривой у нее может не быть квадратиц, их может быть конечное или бесконечное число. Эти соображения делают интересным определение условий существования квадрисекансов или определение границ их числа в различных частных случаях, таких как завязанные кривые, ^[5]^[6] алгебраические кривые, ^[7] или расположение строк . ^[8]

Для особых классов кривых

Узлы и связи

В трехмерном евклидовом пространстве каждый нетривиальный ручной узел или звено имеет квадратиссанс. в случае узловатых многоугольников и гладких узлов Первоначально установленный Эрикой Паннвиц . ^[5]этот результат был распространен на узлы подходящего общего положения и звенья с ненулевым числом зацеплений , ^[6]а позже и ко всем нетривиальным ручным узлам и связям. ^[9]

Панвиц доказал более убедительно, что для локально плоского диска, границей которого является узел, число особенностей диска можно использовать для построения нижней оценки числа различных квадратисектантов. Существование хотя бы одного квадратиссанса следует из того, что любой такой диск должен иметь хотя бы одну особенность. ^[5]^[10] Мортон и Монд (1982) предположили, что число различных квадратисектантов данного узла всегда не менее $n(n-1)/2$ , где $n$ - номер пересечения узла. ^[6]^[10] С тех пор были обнаружены контрпримеры этой гипотезе. ^[10]

Двухкомпонентные связи имеют квадрисекансы, в которых точки квадрисеканса появляются в чередующемся порядке между двумя компонентами. ^[6] а нетривиальные узлы имеют квадрисекансы, в которых четыре точки упорядочены циклически как $abcd$ на узле, появляются по порядку $acbd$ вдоль квадратиссектанта. ^[11] Существование этих чередующихся квадратисектантов можно использовать для вывода теоремы Фари–Милнора , нижней оценки полной кривизны нетривиального узла. ^[11] Квадрисекансы также использовались для определения нижних границ длины узлов. ^[12]

Г.Т. Джин и Х.С. Ким предположили, что, когда кривая с узлами $K$ имеет конечное число квадрисекансов, $K$ может быть аппроксимирован эквивалентным многоугольным узлом с вершинами в точках пересечения квадратисектантов. $K$ , в том же порядке, в котором они появляются на $K$ . Однако их гипотеза ложна: на самом деле для каждого типа узла существует реализация, для которой эта конструкция приводит к самопересекающемуся многоугольнику, и другая реализация, в которой эта конструкция создает узел другого типа. ^[13]

Нерешенная задача по математике :

Имеет ли каждый дикий узел бесконечное число квадратиссектантов?

(еще нерешенные задачи по математике)

Было высказано предположение, что каждый дикий узел имеет бесконечное число квадрисекансов. ^[9]

Алгебраические кривые

Артур Кэли вывел формулу для числа квадратиссансов алгебраической кривой в трехмерном комплексном проективном пространстве в зависимости от ее степени и рода . ^[7] Для кривой степени $d$ и род $g$ , число квадратиссансов равно ^[14] ${\frac {(d-2)(d-3)^{2}(d-4)}{12}}-{\frac {g(d^{2}-7d+13-g)}{2}}.$ Эта формула предполагает, что данная кривая неособая ; корректировки могут потребоваться, если он имеет особые точки. ^[15]^[16]

Наклонить линии

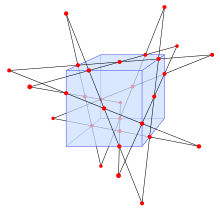
В трехмерном евклидовом пространстве каждый набор из четырех косых линий общего положения имеет либо два квадрисеканса (также в этом контексте называемых трансверсалями ), либо ни одного. Любые три из четырех линий определяют гиперболоид , поверхность с двойной линейкой , в которой один из двух наборов линейчатых линий содержит три заданные линии, а другая линейка состоит из тройных секущих данных линий. Если четвертая из данных прямых пронзает эту поверхность, то она имеет две точки пересечения, поскольку гиперболоид определяется квадратным уравнением . Две трисекансы линейчатой поверхности, проходящие через эти две точки, образуют два квадратиссанса данных четырех прямых. С другой стороны, если четвертая прямая не пересекается с гиперболоидом, то квадратиссектов нет. ^[17] В пространствах с комплексными числовыми координатами, а не с действительными координатами, четыре косые линии всегда имеют ровно два квадратисектанта. ^[8]

Квадрисекты наборов линий играют важную роль в построении двойной шестерки Шлефли — конфигурации из двенадцати линий, пересекающих друг друга в 30 пересечениях. Если пять строк $a_{i}$ (для $i=1,2,3,4,5$ ) заданы в трехмерном пространстве так, что все пять пересекаются общей линией $b_{6}$ но в остальном находятся в общем положении, то каждая из пяти четверок прямых $a_{i}$ имеет второй четырехсекцентный $b_{i}$ , и пять строк $b_{i}$ образованные таким образом, все пересекаются общей линией $a_{6}$ . Эти двенадцать линий и 30 точек пересечения $a_{i}b_{j}$ образуют двойную шестерку. ^[18]^[19]

Договоренность $n$ комплексные линии с заданным числом попарных пересечений и в противном случае перекосом можно интерпретировать как алгебраическую кривую степени $n$ и с родом, определяемым по количеству пересечений, и с использованием вышеупомянутой формулы Кэли для подсчета его квадратицектов. Тот же результат, что и эта формула, можно получить, классифицируя четверки прямых по их пересечениям, подсчитывая количество квадратисексантов для каждого типа четверок и суммируя по всем четверкам прямых в данном множестве. ^[8]

Ссылки

^ Джин, Гё Тэк (декабрь 2017 г.), «Многоугольная аппроксимация узлов квадратисекателями», в Райтере, Филиппе; Блатт, Саймон; Шикорра, Армин (ред.), «Новые направления в геометрической и прикладной теории узлов» , De Gruyter Open, стр. 159–175, doi : 10.1515/9783110571493-008
^ Эйзенбуд, Дэвид ; Харрис, Джо (2016), 3264 и все это: второй курс алгебраической геометрии , Кембридж, Великобритания: Издательство Кембриджского университета, стр. 377, номер домена : 10.1017/CBO9781139062046 , ISBN 978-1-107-60272-4 , МР 3617981
^ Jump up to: Перейти обратно: ^а ^б Уолл, CTC (1977), «Геометрические свойства дифференцируемых многообразий общего положения», в Палисе, Джейкоб; ду Карму, Манфредо (ред.), Геометрия и топология: труды Латиноамериканской школы математики (ELAM III), проводимые в Instituto de Matemática Pura e Aplicada (IMPA), Рио-де-Жанейро, июль 1976 г. , Конспекты лекций по математике, том. 597, стр. 707–774, doi : 10.1007/BFb0085382 , MR 0494233
^ Денн, Элизабет (2018), «Квадрисекансы и существенные секущие узлов», Блатт, Саймон; Райтер, Филипп; Шикорра, Армин (ред.), Новые направления в геометрической и прикладной теории узлов , Уравнения в частных производных и теория меры, Де Грюйтер, Берлин, стр. 138–158, doi : 10.1515/9783110571493-006 , MR 3915943 , S2CID 128222971
^ Jump up to: Перейти обратно: ^а ^б ^с Панвиц, Эрика (1933), «Элементарное геометрическое свойство запутанностей и узлов», Mathematical Annals , 108 (1): 629–672, doi : 10.1007/BF01452857 , S2CID 123026724
^ Jump up to: Перейти обратно: ^а ^б ^с ^д Мортон, Хью Р.; Монд, Дэвид MQ (1982), «Замкнутые кривые без квадратиц», Топология , 21 (3): 235–243, doi : 10.1016/0040-9383(82)90007-6 , MR 0649756
^ Jump up to: Перейти обратно: ^а ^б Кэли, Артур (1863), Философские труды Лондонского королевского общества , том. 153, Королевское общество, стр. 453–483, JSTOR 108806.
^ Jump up to: Перейти обратно: ^а ^б ^с Вонг, BC (1934), «Перечислительные свойства $r$ -пространственные кривые», Бюллетень Американского математического общества , 40 (4): 291–296, doi : 10.1090/S0002-9904-1934-05854-3 , MR 1562839
^ Jump up to: Перейти обратно: ^а ^б Куперберг, Грег (1994), «Квадрисекансы узлов и связей», Журнал теории узлов и ее разветвлений , 3 : 41–50, arXiv : math/9712205 , doi : 10.1142/S021821659400006X , MR 1265452 , S2CID 6103528
^ Jump up to: Перейти обратно: ^а ^б ^с Джин, Гё Таек (2005), «Квадрисекансы узлов с малым числом пересечений», Физические и численные модели в теории узлов (PDF) , сер. Узлы Все, т. 36, Сингапур: World Scientific Publishing, стр. 507–523, doi : 10.1142/9789812703460_0025 , MR 2197955.
^ Jump up to: Перейти обратно: ^а ^б Денн, Элизабет Джейн (2004), Знак чередования квадратиссансов узлов , доктор философии. диссертация, Университет Иллинойса в Урбана-Шампейн , arXiv : math/0510561 , Бибкод : 2005math.....10561D
^ Денн, Элизабет; Дяо, Юанань; Салливан, Джон М. (2006), «Квадрисеканты дают новые нижние границы длины веревки узла» , Geometry & Topology , 10 : 1–26, arXiv : math/0408026 , doi : 10.2140/gt.2006.10.1 , MR 2207788 , S2CID 5770206
^ Бай, Шэн; Ван, Чао; Ван, Цзяцзюнь (2018), «Контрпримеры к гипотезе о квадратичном приближении», Журнал теории узлов и ее разветвлений , 27 (2), 1850022, arXiv : 1605.00538 , doi : 10.1142/S0218216518500220 , MR 3770471 , Идентификатор идентификатора 119601013
^ Гриффитс, Филипп; Харрис, Джозеф (2011), Принципы алгебраической геометрии , Wiley Classics Library, vol. 52, Джон Уайли и сыновья, с. 296, ISBN 9781118030776
^ Уэлчман, В.Г. (апрель 1932 г.), «Заметки о трисекансах и квадрисекансах пространственной кривой», Mathematical Proceedings of the Cambridge Philosophical Society , 28 (2): 206–208, doi : 10.1017/s0305004100010872 , S2CID 120725025
^ Максвелл, Эдвин А. (июль 1935 г.), «Примечание к формуле числа квадратиссектантов кривой в трехмерном пространстве», Mathematical Proceedings of the Cambridge Philosophical Society , 31 (3): 324–326, doi : 10.1017 /s0305004100013086 , S2CID 122279811
^ Гильберт, Дэвид ; Кон-Воссен, Стефан (1952), Геометрия и воображение (2-е изд.), Нью-Йорк: Челси, стр. 164, ISBN 978-0-8284-1087-8
^ Шлефли, Людвиг (1858), Кэли, Артур (ред.), «Попытка определить двадцать семь линий на поверхности третьего порядка и вывести такие поверхности по видам, исходя из реальности линий на поверхности». поверхность» , Ежеквартальный журнал чистой и прикладной математики , 2 : 55–65, 110–120.
^ Коксетер, HSM (2006), «Абсолютное свойство четырех взаимно касающихся окружностей», Неевклидова геометрия , Матем. Прил. (Нью-Йорк), вып. 581, Нью-Йорк: Springer, стр. 109–114, doi : 10.1007/0-387-29555-0_5 , MR 2191243 ; Коксетер повторяет конструкцию Шлефли и приводит несколько ссылок на упрощенные доказательства ее правильности.

[jin17-1] Джин, Гё Тэк (декабрь 2017 г.), «Многоугольная аппроксимация узлов квадратисекателями», в Райтере, Филиппе; Блатт, Саймон; Шикорра, Армин (ред.), «Новые направления в геометрической и прикладной теории узлов» , De Gruyter Open, стр. 159–175, doi : 10.1515/9783110571493-008

[eishar-2] Эйзенбуд, Дэвид ; Харрис, Джо (2016), 3264 и все это: второй курс алгебраической геометрии , Кембридж, Великобритания: Издательство Кембриджского университета, стр. 377, номер домена : 10.1017/CBO9781139062046 , ISBN 978-1-107-60272-4 , МР 3617981

[wall-3] Jump up to: Перейти обратно: ^а ^б Уолл, CTC (1977), «Геометрические свойства дифференцируемых многообразий общего положения», в Палисе, Джейкоб; ду Карму, Манфредо (ред.), Геометрия и топология: труды Латиноамериканской школы математики (ELAM III), проводимые в Instituto de Matemática Pura e Aplicada (IMPA), Рио-де-Жанейро, июль 1976 г. , Конспекты лекций по математике, том. 597, стр. 707–774, doi : 10.1007/BFb0085382 , MR 0494233

[denne-newdir-4] Денн, Элизабет (2018), «Квадрисекансы и существенные секущие узлов», Блатт, Саймон; Райтер, Филипп; Шикорра, Армин (ред.), Новые направления в геометрической и прикладной теории узлов , Уравнения в частных производных и теория меры, Де Грюйтер, Берлин, стр. 138–158, doi : 10.1515/9783110571493-006 , MR 3915943 , S2CID 128222971

[pannwitz-5] Jump up to: Перейти обратно: ^а ^б ^с Панвиц, Эрика (1933), «Элементарное геометрическое свойство запутанностей и узлов», Mathematical Annals , 108 (1): 629–672, doi : 10.1007/BF01452857 , S2CID 123026724

[mm-6] Jump up to: Перейти обратно: ^а ^б ^с ^д Мортон, Хью Р.; Монд, Дэвид MQ (1982), «Замкнутые кривые без квадратиц», Топология , 21 (3): 235–243, doi : 10.1016/0040-9383(82)90007-6 , MR 0649756

[cayley-7] Jump up to: Перейти обратно: ^а ^б Кэли, Артур (1863), Философские труды Лондонского королевского общества , том. 153, Королевское общество, стр. 453–483, JSTOR 108806.

[wong-8] Jump up to: Перейти обратно: ^а ^б ^с Вонг, BC (1934), «Перечислительные свойства $r$ -пространственные кривые», Бюллетень Американского математического общества , 40 (4): 291–296, doi : 10.1090/S0002-9904-1934-05854-3 , MR 1562839

[kuperberg-9] Jump up to: Перейти обратно: ^а ^б Куперберг, Грег (1994), «Квадрисекансы узлов и связей», Журнал теории узлов и ее разветвлений , 3 : 41–50, arXiv : math/9712205 , doi : 10.1142/S021821659400006X , MR 1265452 , S2CID 6103528

[jin-10] Jump up to: Перейти обратно: ^а ^б ^с Джин, Гё Таек (2005), «Квадрисекансы узлов с малым числом пересечений», Физические и численные модели в теории узлов (PDF) , сер. Узлы Все, т. 36, Сингапур: World Scientific Publishing, стр. 507–523, doi : 10.1142/9789812703460_0025 , MR 2197955.

[denne-phd-11] Jump up to: Перейти обратно: ^а ^б Денн, Элизабет Джейн (2004), Знак чередования квадратиссансов узлов , доктор философии. диссертация, Университет Иллинойса в Урбана-Шампейн , arXiv : math/0510561 , Бибкод : 2005math.....10561D

[dds-12] Денн, Элизабет; Дяо, Юанань; Салливан, Джон М. (2006), «Квадрисеканты дают новые нижние границы длины веревки узла» , Geometry & Topology , 10 : 1–26, arXiv : math/0408026 , doi : 10.2140/gt.2006.10.1 , MR 2207788 , S2CID 5770206

[bww-13] Бай, Шэн; Ван, Чао; Ван, Цзяцзюнь (2018), «Контрпримеры к гипотезе о квадратичном приближении», Журнал теории узлов и ее разветвлений , 27 (2), 1850022, arXiv : 1605.00538 , doi : 10.1142/S0218216518500220 , MR 3770471 , Идентификатор идентификатора 119601013

[gh11-14] Гриффитс, Филипп; Харрис, Джозеф (2011), Принципы алгебраической геометрии , Wiley Classics Library, vol. 52, Джон Уайли и сыновья, с. 296, ISBN 9781118030776

[welchman-15] Уэлчман, В.Г. (апрель 1932 г.), «Заметки о трисекансах и квадрисекансах пространственной кривой», Mathematical Proceedings of the Cambridge Philosophical Society , 28 (2): 206–208, doi : 10.1017/s0305004100010872 , S2CID 120725025

[maxwell-16] Максвелл, Эдвин А. (июль 1935 г.), «Примечание к формуле числа квадратиссектантов кривой в трехмерном пространстве», Mathematical Proceedings of the Cambridge Philosophical Society , 31 (3): 324–326, doi : 10.1017 /s0305004100013086 , S2CID 122279811

[hcv-17] Гильберт, Дэвид ; Кон-Воссен, Стефан (1952), Геометрия и воображение (2-е изд.), Нью-Йорк: Челси, стр. 164, ISBN 978-0-8284-1087-8

[schlafli-18] Шлефли, Людвиг (1858), Кэли, Артур (ред.), «Попытка определить двадцать семь линий на поверхности третьего порядка и вывести такие поверхности по видам, исходя из реальности линий на поверхности». поверхность» , Ежеквартальный журнал чистой и прикладной математики , 2 : 55–65, 110–120.

[coxeter-19] Коксетер, HSM (2006), «Абсолютное свойство четырех взаимно касающихся окружностей», Неевклидова геометрия , Матем. Прил. (Нью-Йорк), вып. 581, Нью-Йорк: Springer, стр. 109–114, doi : 10.1007/0-387-29555-0_5 , MR 2191243 ; Коксетер повторяет конструкцию Шлефли и приводит несколько ссылок на упрощенные доказательства ее правильности.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]