Функция Миттаг-Леффлера

Не путать с полиномами Миттаг-Леффлера .

Функцию Миттаг-Леффлера можно использовать для непрерывной интерполяции между гауссовой и лоренцевой функциями.

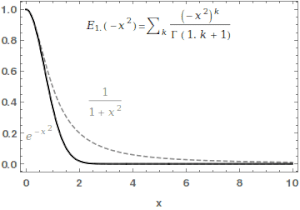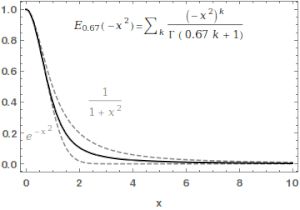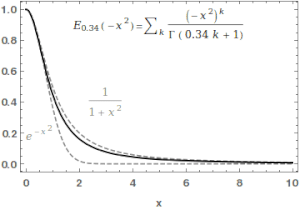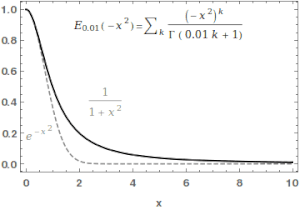
В математике функция Миттаг -Леффлера $E_{\alpha ,\beta }$ это специальная функция , сложная функция , которая зависит от двух комплексных параметров $\alpha$ и $\beta$. Его можно определить следующим рядом , когда действительная часть $\alpha$ является строго положительным:

$E_{\alpha ,\beta }(z)=\sum _{k=0}^{\infty }{\frac {z^{k}}{\Gamma (\alpha k+\beta )}},$

где $\Gamma (x)$ это гамма-функция . Когда $\beta =1$, это сокращается как $E_{\alpha }(z)=E_{\alpha ,1}(z)$.Для $\alpha =0$, приведенный выше ряд равен разложению Тейлора геометрической прогрессии и, следовательно, $E_{0,\beta }(z)={\frac {1}{\Gamma (\beta )}}{\frac {1}{1-z}}$.

В случае $\alpha$ и $\beta$ вещественны и положительны, ряд сходится при всех значениях аргумента $z$, поэтому функция Миттаг-Леффлера представляет собой целую функцию . Эта функция названа в честь Гёста Миттаг-Леффлера . Этот класс функций важен в теории дробного исчисления .

Для $\alpha >0$, функция Миттаг-Леффлера $E_{\alpha ,1}(z)$ это целая функция порядка $1/\alpha$, и в некотором смысле является простейшей целой функцией своего порядка.

Функция Миттаг-Леффлера обладает свойством рекуррентности (теорема 5.1 из )

$E_{\alpha ,\beta }(z)={\frac {1}{z}}E_{\alpha ,\beta -\alpha }(z)-{\frac {1}{z\Gamma (\beta -\alpha )}},$

откуда имеет место следующее асимптотическое разложение Пуанкаре : $0<\alpha <2$ и $\mu$ настоящий такой, что ${\frac {\pi \alpha }{2}}<\mu <\min(\pi ,\pi \alpha )$ тогда для всех $N\in \mathbb {N} ^{*},N\neq 1$, мы можем показать следующие асимптотические разложения (раздел 6. ):

-как $\,|z|\to +\infty ,|{\text{arg}}(z)|\leq \mu$:

$E_{\alpha }(z)={\frac {1}{\alpha }}\exp(z^{\frac {1}{\alpha }})-\sum \limits _{k=1}^{N}{\frac {1}{z^{k}\,\Gamma (1-\alpha k)}}+O\left({\frac {1}{z^{N+1}}}\right)$,

- и как $\,|z|\to +\infty ,\mu \leq |{\text{arg}}(z)|\leq \pi$:

$E_{\alpha }(z)=-\sum \limits _{k=1}^{N}{\frac {1}{z^{k}\Gamma (1-\alpha k)}}+O\left({\frac {1}{z^{N+1}}}\right)$,

где мы использовали обозначение $E_{\alpha }(z)=E_{\alpha ,1}(z)$.

Функция Миттаг-Леффлера, характеризующаяся тремя параметрами, выражается следующим образом:

$E_{\alpha ,\beta }^{\gamma }(z)=\left({\frac {1}{\Gamma (\gamma )}}\right)\sum \limits _{k=1}^{\infty }{\frac {\Gamma (\gamma +k)z^{k}}{k!\Gamma (\alpha k+\beta )}},$

где $\alpha ,\beta$ и $\gamma$ являются комплексными параметрами и $\Re (\alpha )>0$.

Для $\gamma \in \mathbb {N}$, функция Миттаг-Леффлера с тремя параметрами переформулируется как:

$E_{\alpha ,\beta }^{\gamma }(z)=\sum _{k=0}^{\infty }{\frac {(\gamma )_{k}z^{k}}{k!\Gamma (\alpha k+\beta )}},$

где $(\gamma )_{k}:={\frac {\Gamma (\gamma +k)}{\Gamma (\gamma )}}=\gamma (\gamma +1)\cdots (\gamma +k-1)$ и он демонстрирует следующее свойство:

$E_{(\alpha ,\beta )}^{\gamma }(z)={\frac {1}{\alpha ^{\gamma }}}\left(E_{(\alpha ,\beta -1)}^{\gamma -1}(z)+(1-\beta +\alpha \gamma )E_{(\alpha ,\beta )}^{\gamma -1}(z)\right)$.

Кроме того, связь с первым параметром 2-параметрической функции Миттаг-Леффлера следующая: $E_{(\alpha ,\beta )}(rt^{\alpha })={\frac {1}{m}}\sum _{i=1}^{m}E_{(\rho ,\beta )}(s_{i}t^{\rho }),$

где ${\frac {\alpha }{\rho }}=m\in \mathbb {N}$ и $s_{i}$ являются корнями $s^{m}=r$.

Особые случаи

Для $\alpha =0,1/2,1,2$ находим: (раздел 2 )

Функция ошибки :

$E_{\frac {1}{2}}(z)=\exp(z^{2})\operatorname {erfc} (-z).$

Сумма геометрической прогрессии :

$E_{0}(z)=\sum _{k=0}^{\infty }z^{k}={\frac {1}{1-z}},\,|z|<1.$

Экспоненциальная функция :

$E_{1}(z)=\sum _{k=0}^{\infty }{\frac {z^{k}}{\Gamma (k+1)}}=\sum _{k=0}^{\infty }{\frac {z^{k}}{k!}}=\exp(z).$

Гиперболический косинус :

$E_{2}(z)=\cosh({\sqrt {z}}),{\text{ and }}E_{2}(-z^{2})=\cos(z).$

Для $\beta =2$, у нас есть

$E_{1,2}(z)={\frac {e^{z}-1}{z}},$

$E_{2,2}(z)={\frac {\sinh({\sqrt {z}})}{\sqrt {z}}}.$

Для $\alpha =0,1,2$, интеграл

$\int _{0}^{z}E_{\alpha }(-s^{2})\,{\mathrm {d} }s$

дает соответственно: $\arctan(z)$, ${\tfrac {\sqrt {\pi }}{2}}\operatorname {erf} (z)$, $\sin(z)$.

-Леффлера

Интегральное представление функции Миттаг-Леффлера имеет вид (раздел 6 книги )

$E_{\alpha ,\beta }(z)={\frac {1}{2\pi i}}\oint _{C}{\frac {t^{\alpha -\beta }e^{t}}{t^{\alpha }-z}}\,dt,\Re (\alpha )>0,\Re (\beta )>0,$

где контур $C$ начинается и заканчивается в $-\infty$ и обводит особенности и точки ветвления подынтегральной функции.

С преобразованием Лапласа и суммированием Миттаг-Леффлера связано выражение (уравнение (7.5) с $m=0$)

$\int _{0}^{\infty }e^{-tz}t^{\beta -1}E_{\alpha ,\beta }(\pm r\,t^{\alpha })\,dt={\frac {z^{\alpha -\beta }}{z^{\alpha }\mp r}},\Re (z)>0,\Re (\alpha )>0,\Re (\beta )>0.$

Применение функции Миттаг-Леффлера

Одним из применений функции Миттаг-Леффлера является моделирование вязкоупругих материалов дробного порядка. Экспериментальные исследования нестационарного релаксационного поведения вязкоупругих материалов характеризуются очень быстрым снижением напряжения в начале процесса релаксации и чрезвычайно медленным затуханием на больших временах. Прежде чем будет достигнуто постоянное асимптотическое значение, может даже пройти много времени. Следовательно, для описания релаксационного поведения с достаточной точностью требуется множество элементов Максвелла. Это заканчивается сложной задачей оптимизации для идентификации большого количества параметров материала. было введено понятие дробных производных С другой стороны, с годами в теорию вязкоупругости . Среди этих моделей дробная модель Зинера оказалась очень эффективной для прогнозирования динамической природы резиноподобных материалов с использованием лишь небольшого количества параметров материала. Решение соответствующего материального уравнения приводит к релаксационной функции типа Миттаг-Леффлера. Это определяется степенной ряд с отрицательными аргументами. Эта функция отражает все существенные свойства процесса релаксации под действием произвольного и непрерывного сигнала со скачком в начале координат.

См. также

• Суммирование Миттаг-Леффлера
• Распределение Миттаг-Леффлера
• Функция Фокса – Райта
• Функция Прабхакара

Примечания

• R Пакет «MittagLeffleR», автор: Гуртек Гилл, Питер Страка. Реализует функцию Миттаг-Леффлера, распределение, генерацию случайных величин и оценку.

Ссылки

• Миттаг-Леффлер, М.Г.: О новой функции E(x). ЧР акад. наук. Париж 137, 554–558 (1903)
• Миттаг-Леффлер, М.Г.: Над функцией E˛.x/. Урожай. Р. Линчеи, (Сер. 5) 13, 3–5 (1904).
• Горенфло Р., Килбас А.А., Майнарди Ф., Рогосин С.В., Функции Миттаг-Леффлера, смежные темы и приложения (Springer, Нью-Йорк, 2014) 443 страницы ISBN   978-3-662-43929-6
• Игорь Подлубный (1998). «глава 1». Дробные дифференциальные уравнения. Введение в дробные производные, дробно-дифференциальные уравнения, некоторые методы их решения и некоторые их приложения . Математика в науке и технике. Академическая пресса. ISBN  0-12-558840-2 .
• Кай Дитхельм (2010). «глава 4». Анализ дробных дифференциальных уравнений: прикладное изложение с использованием дифференциальных операторов типа Капуто . Конспект лекций по математике. Гейдельберг и Нью-Йорк: Springer-Verlag. ISBN  978-3-642-14573-5 .

Внешние ссылки

• Функция Миттаг-Леффлера: код MATLAB
• Миттаг-Леффлер и стабильные случайные числа: случайные блуждания в непрерывном времени и стохастическое решение уравнений дробной диффузии пространства-времени

Эта статья включает в себя материал из функции Миттаг-Леффлера на PlanetMath , которая распространяется по лицензии Creative Commons Attribution/Share-Alike License .