Проблема с джипом

Проблема джипом с ^[1] проблема пересечения пустыни ^[2] или проблема с исследованием ^[3] — это математическая задача, в которой джип должен максимально увеличить расстояние, которое он может преодолеть в пустыне с заданным количеством топлива. Джип может перевозить только фиксированное и ограниченное количество топлива, но он может оставлять топливо и собирать топливо на топливных свалках в любой точке пустыни.

Проблема впервые появилась в сборнике 9-го века Propositiones ad Acuendos Juvenes ( «Проблемы для заострения молодежи »), приписываемом Алкуину , где загадка заключалась в том, что путешествующий верблюд ест зерно. ^[4] В «De viribus quantitatis» (ок. 1500 г.) Луки Пачоли также обсуждается эта проблема. Современное лечение было предложено Н. Дж. Файном в 1947 году. ^[1]

Проблема

На постоянной базе хранится n единиц топлива. Джип может перевозить не более 1 единицы топлива в любой момент времени и может проехать 1 единицу расстояния на 1 единице топлива (расход топлива джипа считается постоянным). В любой момент поездки джип может оставить любое количество топлива, которое он перевозит, на свалке топлива или может собрать любое количество топлива, которое было оставлено на свалке во время предыдущей поездки, при условии, что его загрузка топлива никогда не превышает 1 единица. Есть два варианта проблемы:

Исследование пустыни – джип должен возвращаться на базу в конце каждой поездки.
Пересечение пустыни — джип должен вернуться на базу в конце каждой поездки, за исключением последней поездки, когда джип проезжает как можно дальше, прежде чем у него закончится топливо.

В любом случае цель состоит в том, чтобы максимизировать расстояние, пройденное джипом в его последнем путешествии. В качестве альтернативы, цель может состоять в том, чтобы найти наименьшее количество топлива, необходимое для окончательного путешествия на заданное расстояние.

Вариации

В классической задаче топливо в джипе и на свалках рассматривается как непрерывное количество. Были предложены более сложные варианты проблемы, в которых топливо можно оставлять или собирать только в дискретных количествах. ^[5]

Решение

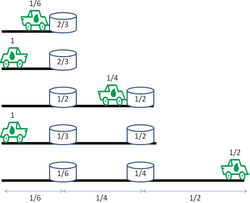
Стратегия, позволяющая максимально увеличить пройденное расстояние в последнем путешествии для варианта «исследования пустыни», заключается в следующем:

Джип совершает n поездок. В каждую поездку он стартует с базы с 1 единицей топлива.
За первую поездку джип проезжает расстояние 1/(2 n ) единиц и оставляет на топливной свалке ( n − 1)/ n единиц топлива. У джипа еще осталось 1/(2 n ) единиц топлива – ровно столько, чтобы вернуться на базу.
В каждой из последующих n − 1 поездок джип забирает 1/(2 n на выходе он также собирает 1/(2 n ) единиц топлива из этой первой топливной свалки, чего как раз достаточно для возвращения на базу. ) единиц топлива из этой первой топливной свалки, так что он покидает топливную свалку с 1 единицей топлива. На обратном пути
Во второй поездке джип доезжает до первой топливной свалки и заправляется. Затем он проходит расстояние 1/(2 n - 2) единиц и оставляет ( n - 2)/( n - 1) единиц топлива на второй складе топлива. У джипа еще осталось 1/(2 n − 2) единиц топлива, чего как раз хватит, чтобы вернуться на первую свалку. Здесь он собирает 1/(2 n ) единиц топлива, чего как раз достаточно для возвращения на базу.
В каждой из последующих n − 2 поездок джип забирает 1/(2 n на выходе − 2) единиц топлива из этой второй топливной свалки, так что он покидает топливную свалку с 1 единицей топлива. На обратном пути он также забирает 1/(2 n − 2) единиц топлива со второй свалки, чего как раз достаточно для возврата на первую свалку.
Джип продолжает движение таким образом, так что в поездке k он устанавливает новую k -ю свалку топлива на расстоянии 1/(2 n − 2 k + 2) единиц от предыдущей свалки топлива и покидает ( n − k )/( n − k + 1) единиц топлива. В каждом из последующих n − k рейсов он забирает 1/(2 n − 2 k + 2) единиц топлива с k -й свалки на выходе и еще 1/(2 n − 2 k + 2) единиц топлива. на обратном пути.

Когда джип отправляется в последний путь, имеется n − 1 свалок топлива. Самая дальняя содержит 1/2 единицы топлива, следующая — 1/3 единицы топлива и так далее, а на ближайшей свалке топлива осталось всего 1/ n единиц топлива. Вместе с 1 единицей топлива, с которой он стартует с базы, это означает, что джип может проехать общее расстояние туда и обратно, равное

1+{\frac {1}{2}}+{\frac {1}{3}}+\cdots +{\frac {1}{n}}=\sum _{k=1}^{n}{\frac {1}{k}}\equiv 2\times \mathrm {explore} (n)

отряды в последний путь (максимальное расстояние, пройденное в пустыню, составляет половину этого расстояния). ^[3] На каждой свалке на выходе он собирает половину оставшегося топлива, которое и заполняет его бак. Покинув самую дальнюю свалку горючего, он проходит еще 1/2 единицы дальше в пустыню, а затем возвращается к самой дальней свалке горючего. На обратном пути он собирает остатки топлива с каждой склада топлива, которого как раз хватает для того, чтобы добраться до следующей склада топлива или, на последнем этапе, вернуться на базу.

Расстояние, пройденное во время последней поездки, равно n- й гармоники номеру H _n . Поскольку числа гармоник не ограничены, в последнем путешествии можно превысить любое заданное расстояние, если на базе имеется достаточно топлива. Однако количество требуемого топлива и количество свалок топлива увеличиваются экспоненциально с увеличением пройденного расстояния.

Вариант «пересечение пустыни» можно решить с помощью аналогичной стратегии, за исключением того, что теперь нет необходимости собирать топливо на обратном пути в последнем путешествии. Таким образом, в поездке k джип устанавливает новую k -ю свалку топлива на расстоянии 1/(2 n − 2 k + 1) единиц от предыдущей свалки топлива и покидает (2 n − 2 k − 1)/(2 n − 2к + 1 ) единиц топлива нет. В каждом из следующих n − k − 1 рейсов он забирает 1/(2 n − 2 k + 1) единиц топлива с k -й свалки на выходе и еще 1/(2 n − 2 k + 1) единиц топлива. топлива на обратном пути.

Теперь, когда джип отправляется в последний путь, имеется n − 1 свалок топлива. В самой дальней находится 1/3 единицы топлива, в следующей — 1/5 единицы топлива и так далее, а на ближайшей свалке топлива осталось всего 1/(2 n − 1) единицы топлива. Вместе с 1 единицей топлива, с которой он стартует с базы, это означает, что джип может проехать общее расстояние

1+{\frac {1}{3}}+{\frac {1}{5}}+\cdots +{\frac {1}{2n-1}}=\sum _{k=1}^{n}{\frac {1}{2k-1}}=H_{2n-1}-{\frac {1}{2}}H_{n-1}\equiv \mathrm {cross} (n)

подразделения в свой последний поход. ^[1]^[3] Он собирает на каждой свалке на выходе все оставшееся топливо, которое заполняет его бак. Покинув самую дальнюю свалку топлива, он проходит расстояние еще в 1 единицу.

Обратите внимание, что

\mathrm {cross} (n)=\sum _{k=1}^{n}{\frac {1}{2k-1}}>\sum _{k=1}^{n}{\frac {1}{2k}}={\frac {1}{2}}H_{n}=\mathrm {explore} (n)

так что теоретически можно пересечь пустыню любого размера, имея достаточно топлива на базе. Как и раньше, количество требуемого топлива и количество свалок топлива увеличиваются экспоненциально с увеличением пройденного расстояния.

Таким образом, максимальное расстояние, которое может преодолеть джип (с запасом топлива на 1 единицу расстояния в любой момент времени) за n поездок (с n-1 промежуточными свалками топлива и общим потреблением n единиц топлива) равно

$\mathrm {explore} (n)={\frac {1}{2}}H_{n}={\frac {1}{2}}+{\frac {1}{4}}+{\frac {1}{6}}+\cdots +{\frac {1}{2n}}$ , для исследования пустыни, где джип должен возвращаться на базу в конце каждой поездки;
$\mathrm {cross} (n)=H_{2n-1}-{\frac {1}{2}}H_{n-1}=1+{\frac {1}{3}}+{\frac {1}{5}}+\cdots +{\frac {1}{2n-1}}$ , для пересечения пустыни, где джип должен вернуться на базу в конце каждой поездки, за исключением последней поездки, когда джип проезжает как можно дальше, прежде чем у него закончится топливо.

Здесь $H_{n}=1+{\frac {1}{2}}+{\frac {1}{3}}+\cdots +{\frac {1}{n}}$ — номер n-й гармоники .

Постоянное количество топлива

Количество единиц топлива, имеющихся на базе, не обязательно должно быть целым числом. В общем случае максимальное расстояние, достижимое для задачи «исследовать пустыню» с $n$ единицами топлива, равно

\mathrm {explore} (n)=\int _{0}^{n}{\frac {\mathrm {d} f}{2\lceil n-f\rceil }}

с первым складом топлива, расположенным в г. $\{n\}/(2\lceil n\rceil )$ единиц расстояния от стартовой базы, вторая в $1/(2\lceil n\rceil -2)$ единиц расстояния от первой свалки топлива, третьей от $1/(2\lceil n\rceil -4)$ единицы расстояния от второй свалки топлива и так далее. Здесь $\{n\}=n-\lfloor n\rfloor$ является дробной частью $n$ .

Максимальное расстояние, достижимое для задачи «пересечь пустыню» с $n$ единицами топлива, равно

\mathrm {cross} (n)=\int _{0}^{n}{\frac {\mathrm {d} f}{2\lceil n-f\rceil -1}}

с первым складом топлива, расположенным в г. $\{n\}/(2\lceil n\rceil -1)$ единиц расстояния от стартовой базы, вторая в $1/(2\lceil n\rceil -3)$ единиц расстояния от первой свалки топлива, третьей от $1/(2\lceil n\rceil -5)$ единицы расстояния от второй свалки топлива и так далее. Здесь $\{n\}=n-\lfloor n\rfloor$ является дробной частью $n$ .

Независимость ордена

Обратите внимание, что порядок поездок на джипах не фиксирован. Например, в версии задачи «исследование пустыни» джип может совершить $n - 1$ поездок туда и обратно между базой и первой свалкой топлива, каждый раз оставляя $(n - 1)/ n$ единиц топлива на свалке. а затем совершить $n$ -ю поездку в одну сторону до первой склада топлива, прибыв туда с общим количеством $(n - 1) + 1/(2 n)$ единиц топлива. 1 $/(2 n)$ единиц откладываются для обратного пути на базу в самом конце, а остальные $n - 1$ единиц топлива используются для перемещения топлива между первой и второй складами топлива, используя $n - 2$ поездки туда и обратно и затем $(n -1)$ -я поездка в одну сторону до второй склада топлива. И так далее.

Практическое применение

В ходе *операции Black Buck One* атакующий «Вулкан» семь раз дозаправлялся на обратном пути и один раз на обратном пути. Серые линии обозначают резервные самолеты для замены раненых.

Эта проблема может иметь практическое применение в условиях военного времени, особенно в отношении эффективности использования топлива . В контексте бомбардировок Японии во время Второй мировой войны самолетами B-29 , Роберт Макнамара в фильме «Туман войны» говорит что понимание проблемы топливной эффективности, вызванной необходимостью транспортировки топлива на передовые базы, было основной причиной, почему стратегия от бомбардировок материкового Китая отказались в пользу стратегии прыжков по островам :

«Мы должны были переправить эти самолеты с баз в Канзасе в Индию. Затем нам пришлось переправить топливо через горб в Китай. [...] Мы должны были взять эти B-29 — там не было самолетов-заправщиков . Мы должны были заправить их топливом, вылететь из Индии в Чэнту ; выгрузить топливо; совершить достаточное количество миссий, чтобы накопить топливо в Чэнту; перелететь в Явату , Япония ; разбомбить сталелитейные заводы и вернуться в Индию;У нас было так мало подготовки по этой проблеме максимизации [топливной] эффективности, что мы фактически обнаружили, что для того, чтобы вернуть часть B-29 вместо выгрузки топлива, им пришлось взять его на себя. Короче говоря, оно того не стоило. И именно ЛеМэй действительно пришел к такому выводу и побудил «Чифс» перенести все это на Марианские острова , что опустошило Японию». ^[6]

( Миссии по атомной бомбардировке в конце Второй мировой войны проводились с использованием самолетов B-29 Superfortress с тихоокеанского острова Тиниан на Северных Марианских островах .)

См. также

Прочтите «Операцию Черный Бак», чтобы лучше понять применение этих идей. В этих миссиях, проведенных во время Фолклендской войны , Королевские ВВС использовали дозаправку в воздухе, размещая танкеры, чтобы позволить бомбардировщикам Vulcan, базирующимся на острове Вознесения, бомбить цели на Фолклендских островах .
Гармонический ряд (математика)
Оптимизация (математика)

Ссылки

^ Jump up to: Перейти обратно: ^а ^б ^с Вайсштейн, Эрик В. «Проблема с джипом» . Математический мир .
^ Гарднер, Мартин (1994). Мои лучшие математические и логические задачи . Дувр. стр. 53 . ISBN 0-486-28152-3 .
^ Jump up to: Перейти обратно: ^а ^б ^с « Проблемы разведки. Другой распространенный вопрос касается максимального расстояния в пустыне, на которое может добраться из приграничного поселения исследователь, способный нести с собой припасы, которых хватит ему на несколько дней». WW Роуз Болл и HSM Коксетер (1987). Математические развлечения и очерки , тринадцатое издание, Дувр, стр. 32. ISBN 0-486-25357-0 .
↑ « Проблемы для обострения молодежи» , Джон Хэдли и Дэвид Сингмастер, The Mathematical Gazette , 76 , № 475 (март 1992 г.), стр. 102–126.
^ Оптимальная логистика для экспедиций: проблема джипа с полной заправкой , Гюнтер Роте и Гоочуань Чжан, июнь 1996 г.
^ Стенограмма «Тумана войны» , www.errolmorris.com

[wolfram-1] Jump up to: Перейти обратно: ^а ^б ^с Вайсштейн, Эрик В. «Проблема с джипом» . Математический мир .

[2] Гарднер, Мартин (1994). Мои лучшие математические и логические задачи . Дувр. стр. 53 . ISBN 0-486-28152-3 .

[coxeter-3] Jump up to: Перейти обратно: ^а ^б ^с « Проблемы разведки. Другой распространенный вопрос касается максимального расстояния в пустыне, на которое может добраться из приграничного поселения исследователь, способный нести с собой припасы, которых хватит ему на несколько дней». WW Роуз Болл и HSM Коксетер (1987). Математические развлечения и очерки , тринадцатое издание, Дувр, стр. 32. ISBN 0-486-25357-0 .

[a-4] ↑ « Проблемы для обострения молодежи» , Джон Хэдли и Дэвид Сингмастер, The Mathematical Gazette , 76 , № 475 (март 1992 г.), стр. 102–126.

[5] Оптимальная логистика для экспедиций: проблема джипа с полной заправкой , Гюнтер Роте и Гоочуань Чжан, июнь 1996 г.

[6] Стенограмма «Тумана войны» , www.errolmorris.com

[1]

[2]

[3]

[4]

[5]

[6]