Динамика полета космического корабля

Эта статья о динамике полета космических аппаратов. О динамике полета самолета см. Динамика полета самолета . Для управления ориентацией космического корабля см. Управление ориентацией .

Траектория полета миссии «Аполлон-11» , высадившейся на Луну, июль 1969 г.

Динамика полета космического корабля — это применение механической динамики для моделирования того, как внешние силы, действующие на космический корабль или космический корабль, определяют траекторию его полета. Эти силы в основном бывают трех типов: движущая сила, создаваемая двигателями транспортного средства; гравитационная сила, действующая на Землю и другие небесные тела; и аэродинамическая подъемная сила и сопротивление (при полете в атмосфере Земли или другого тела, например Марса или Венеры).

Принципы динамики полета используются для моделирования полета транспортного средства с двигателем во время запуска с Земли; орбитальный полет космического корабля; маневры по изменению орбиты; транслунный и межпланетный перелет; запуск и посадка на небесное тело с атмосферой или без нее; вход через атмосферу Земли или другого небесного тела; и контроль отношения . корабля Обычно они запрограммированы в инерциальные навигационные системы и контролируются на земле членом группы диспетчеров полета , известным в НАСА как офицер по динамике полета , или в Европейском космическом агентстве как штурман космического корабля.

Динамика полета зависит от дисциплин двигательной техники, аэродинамики и астродинамики ( орбитальная механика и небесная механика ). Его нельзя свести к простому контролю отношения; Настоящие космические корабли не имеют рулевых колес и румпелей, как самолеты или корабли. В отличие от того, как изображаются вымышленные космические корабли, космический корабль на самом деле не кренится для разворота в космическом пространстве, где траектория его полета строго зависит от действующих на него гравитационных сил и применяемых движущих маневров .

Основные принципы

Полет космического корабля определяется применением Ньютона второго закона движения : $$\mathbf {F} =m\mathbf {a} ,$$где F — векторная сумма всех сил, действующих на транспортное средство, m — его текущая масса, а — вектор ускорения, мгновенная скорость изменения скорости ( v ), которая, в свою очередь, является мгновенной скоростью изменения смещения. При решении задачи ускорение равно сумме сил, деленной на массу. Ускорение интегрируется по времени, чтобы получить скорость, а скорость, в свою очередь, интегрируется для определения положения.

Расчеты динамики полета выполняются компьютеризированными системами наведения на борту корабля; Состояние динамики полета контролируется на земле во время силовых маневров членом группы диспетчеров полета, известным в как НАСА Центре пилотируемых космических полетов офицер по динамике полета , или в Европейском космическом агентстве как штурман космического корабля.

При полете в атмосфере с двигателем на транспортное средство действуют три основные силы: движущая сила , аэродинамическая сила и гравитация . Другие внешние силы, такие как центробежная сила , сила Кориолиса и давление солнечного излучения , как правило, незначительны из-за относительно короткого времени полета с двигателем и небольшого размера космического корабля, и ими обычно можно пренебречь при упрощенных расчетах производительности.

Движение

Тяга ракетного двигателя в общем случае работы в атмосфере аппроксимируется выражением:

$$F={\dot {m}}\;v_{e}={\dot {m}}\;v_{\text{e-opt}}+A_{e}(p_{e}-p_{\text{amb}})$$где,

• ${\dot {m}}$ это массовый расход выхлопных газов
• $v_{e}$ - эффективная скорость истечения (иногда обозначается иначе как c ) в публикациях
• $v_{\text{e-opt}}$ — эффективная скорость струи, когда p _amb = p _e
• $A_{e}$— площадь потока в плоскости выхода из сопла (или плоскость, в которой струя выходит из сопла, если поток разделен)
• $p_{e}$ статическое давление в плоскости среза сопла
• $p_{\text{amb}}$ это окружающее (или атмосферное) давление

Эффективная скорость истечения ракетного топлива пропорциональна удельному импульсу вакуума и зависит от атмосферного давления: $$v_{e}=g_{0}\left(I_{\text{sp-vac}}-{\frac {A_{e}\,p_{\text{amb}}}{\dot {m}}}\right)$$

где:

• $I_{\text{sp-vac}}$ имеет единицы секунды
• $g_{0}$ это гравитационное ускорение на поверхности Земли

Удельный импульс связывает мощность дельта-v с количеством израсходованного топлива в соответствии с уравнением ракеты Циолковского : $$\Delta v\ =v_{e}\ln {\frac {m_{0}}{m_{1}}}$$где:

• $m_{0}$ - начальная общая масса, включая топливо, в кг (или фунтах).
• $m_{1}$ конечная общая масса в кг (или фунтах)
• $v_{e}$ - эффективная скорость выхлопа в м/с (или футах/с)
• $\Delta v$ это дельта-v в м/с (или футах/с)

Аэродинамическая сила

Аэродинамические силы , присутствующие вблизи тела со значительной атмосферой, такого как Земля , Марс или Венера , анализируются как: подъемная сила , определяемая как составляющая силы, перпендикулярная направлению полета (не обязательно вверх, чтобы уравновесить гравитацию, как в самолете); и перетащите компонент параллельно и в противоположном направлении полета. Подъемная сила и сопротивление моделируются как произведение коэффициента на динамическое давление, действующее на опорную область: $$\mathbf {L} =C_{L}qA_{\text{ref}}$$$$\mathbf {D} =C_{D}qA_{\text{ref}}$$

где:

• CL _{, углом атаки между} примерно линейна с α осью транспортного средства и направлением полета (до предельного значения), и равна 0 при α = 0 для осесимметричного тела;
• C _D меняется в зависимости от α ² ;
• C _L и CD _числа изменяются в зависимости от Рейнольдса и числа Маха ;
• q , динамическое давление, равно 1/2 ρv ² , где ρ — плотность атмосферы, смоделированная для Земли как функция высоты в Международной стандартной атмосфере (с использованием предполагаемого распределения температуры, изменения гидростатического давления и закона идеального газа ); и
• Ссылка _— это характерная площадь транспортного средства, например площадь поперечного сечения при максимальном диаметре.

Гравитация

Гравитационная сила, которую небесное тело оказывает на космический аппарат, моделируется с использованием тела и транспортного средства как точечных масс; тела (Земля, Луна и т. д.) упрощены до сфер; а масса транспортного средства намного меньше массы тела, так что ее влиянием на ускорение свободного падения можно пренебречь. Следовательно, сила гравитации рассчитывается по формуле:

$$\mathbf {W} =m\cdot g$$

где:

• $W$ – сила гравитации (вес);
• $m$ – масса космического корабля; и
• $r$ – радиальное расстояние аппарата до центра планеты; и
• $r_{0}$ – радиальное расстояние от поверхности планеты до ее центра; и
• $g_{0}$ гравитационное ускорение на поверхности планеты
• g — гравитационное ускорение на высоте, которое изменяется обратно пропорционально квадрату радиального расстояния до центра планеты: $$g=g_{0}\left({\frac {r_{0}}{r}}\right)^{2}$$

Моторизованный полет

Уравнения движения, используемые для описания полета транспортного средства с двигателем во время запуска, могут быть такими сложными, как шесть степеней свободы для расчетов в полете, или такими простыми, как две степени свободы для предварительных оценок характеристик. В полетных расчетах будут учитываться такие факторы возмущения Земли , как сжатие и неравномерное распределение массы; и гравитационные силы всех близлежащих тел, включая Луну, Солнце и другие планеты. Предварительные оценки позволяют сделать некоторые упрощающие предположения: планета сферическая, однородная; транспортное средство можно представить в виде точечной массы; решение траектории полета представляет собой задачу двух тел ; и локальная траектория полета лежит в одной плоскости) с достаточно небольшой потерей точности.

Векторы скорости, положения и силы, действующие на космический аппарат во время запуска

В общем случае запуска с Земли необходимо учитывать тягу двигателя, аэродинамические силы и гравитацию. Уравнение ускорения можно преобразовать из векторной в скалярную форму, разложив его в тангенциальную (скорость $v$) и угловые (угол траектории полета $\theta$ относительно местной вертикали) компоненты скорости изменения времени относительно стартовой площадки. Таким образом, два уравнения становятся:

$${\begin{aligned}{\dot {v}}&={\frac {F\cos \alpha }{m}}-{\frac {D}{m}}-g\cos \theta \\{\dot {\theta }}&={\frac {F\sin \alpha }{mv}}+{\frac {L}{mv}}+\left({\frac {g}{v}}-{\frac {v}{r}}\right)\sin \theta ,\end{aligned}}$$

где:

• F – тяга двигателя;
• α — угол атаки;
• m – масса автомобиля;
• D автомобиля — аэродинамическое сопротивление ;
• L – его аэродинамическая подъемная сила ;
• r — радиальное расстояние до центра планеты; и
• g — ускорение свободного падения на высоте.

Масса уменьшается по мере расходования топлива и ступеней ракеты сброса , двигателей или баков (если применимо).

Зафиксированные на планете значения v и θ в любой момент полета затем определяются путем численного интегрирования двух уравнений скорости от нулевого времени (когда оба v и θ равны 0): $${\begin{aligned}v&=\int _{t_{0}}^{t}{\dot {v}}\,dt\\\theta &=\int _{t_{0}}^{t}{\dot {\theta }}\,dt\end{aligned}}$$

Анализ методом конечных элементов можно использовать для интегрирования уравнений, разбивая полет на небольшие временные интервалы.

Для большинства ракет-носителей создаются относительно небольшие уровни подъемной силы и используется гравитационный разворот , который в основном зависит от третьего члена уравнения угловой скорости. В момент взлета, когда угол и скорость равны нулю, уравнение тета-точки математически неопределенно и не может быть вычислено до тех пор, пока скорость не станет ненулевой вскоре после взлета. Но обратите внимание, что в этом случае единственной силой, которая может вызвать опрокидывание транспортного средства, является тяга двигателя, действующая при ненулевом угле атаки (первый член) и, возможно, небольшой подъемной силе (второй член), пока не достигается нулевой угол тангажа. При гравитационном развороте тангаж инициируется увеличением угла атаки (посредством тяги двигателя на подвесе ), за которым следует постепенное уменьшение угла атаки на протяжении оставшейся части полета.

Если известны скорость и угол траектории полета, высота $h$ и расстояние вниз по дальности $s$ вычисляются как:

Векторы скорости и силы, действующие на космический аппарат при механизированном спуске и посадке

$${\begin{aligned}h&=\int _{t_{0}}^{t}v\cos \theta \,dt\\r&=r_{0}+h\\s&=r_{0}\int _{t_{0}}^{t}{\frac {v}{r}}\sin \theta \,dt\end{aligned}}$$

, фиксированные на планете, Значения v и θ преобразуются в фиксированные в пространстве (инерциальные) значения с помощью следующих преобразований: $$v_{s}={\sqrt {v^{2}+2\omega rv\cos \varphi \sin \theta \sin A_{z}+(\omega r\cos \theta )^{2}}},$$где ω — скорость вращения планеты в радианах в секунду, φ — широта стартовой площадки, а A _z запуска — угол азимута . $$\theta _{s}=\arccos \left({\frac {v\cos \theta }{v_{s}}}\right)$$

Конечные v _s , θ _s и r должны соответствовать требованиям целевой орбиты, как это определено орбитальной механикой (см. Орбитальный полет выше), где конечный v _s обычно представляет собой требуемую перицентрическую (или круговую) скорость, а конечный θ _s равен 90. градусов. При анализе механизированного спуска будет использоваться та же процедура, но с обратными граничными условиями.

Орбитальный полет

Дополнительная информация: Орбитальная механика.

Орбитальная механика используется для расчета полета по орбите вокруг центрального тела. Для достаточно высоких орбит (обычно не менее 190 километров (100 морских миль) в случае Земли) аэродинамическую силу можно считать незначительной для относительно краткосрочных миссий (хотя может присутствовать небольшое сопротивление, которое приводит к затуханию орбиты). орбитальной энергии в течение более длительных периодов времени.) Когда масса центрального тела намного больше массы космического корабля, а другие тела находятся достаточно далеко, решение орбитальных траекторий можно рассматривать как задачу двух тел.

Можно показать, что в идеале траектория представляет собой коническое сечение (круг, эллипс, парабола или гипербола). с центральным телом, расположенным в одном фокусе. Орбитальные траектории представляют собой круги или эллипсы; параболическая траектория представляет собой первый выход транспортного средства из гравитационного поля центрального тела. Гиперболические траектории представляют собой траектории ухода с избыточной скоростью и будут рассмотрены ниже в разделе « Межпланетный полет» .

Эллиптические орбиты характеризуются тремя элементами. Большая полуось a представляет собой среднее значение радиуса в апоцентре и перицентре : $$a={\frac {r_{a}+r_{p}}{2}}$$

Затем эксцентриситет можно e рассчитать для эллипса, зная апсиды: $$e={\frac {r_{a}}{a}}-1$$

Период времени для полной орбиты зависит только от большой полуоси и не зависит от эксцентриситета: $$T=2\pi {\sqrt {\frac {a^{3}}{\mu }}}$$где $\mu$ — стандартный гравитационный параметр центрального тела.

Угловые элементы орбиты космического корабля, вращающегося вокруг центрального тела, определяющие ориентацию орбиты относительно ее фундаментальной базовой плоскости.

Ориентация орбиты в пространстве задается тремя углами:

• Наклонение . i орбитальной плоскости к фундаментальной плоскости (обычно это экваториальная плоскость планеты или Луны, или, в случае солнечной орбиты, плоскость орбиты Земли вокруг Солнца, известная как эклиптика ) . Положительное наклонение — к северу , а отрицательный наклон направлен на юг.
• Долгота восходящего узла Ω, измеренная в фундаментальной плоскости против часовой стрелки, если смотреть на юг, от исходного направления (обычно точки весеннего равноденствия ) до линии, где космический корабль пересекает эту плоскость с юга на север. (Если наклон равен нулю, этот угол не определен и принимается равным 0.)
• Аргумент периапсиса ω , измеренный в плоскости орбиты против часовой стрелки, смотрящей на юг, от восходящего узла к периапсису. Если наклон равен 0, восходящего узла нет, поэтому ω измеряется от опорного направления. Для круговой орбиты перицентр отсутствует, поэтому ω принимается равным 0.

Плоскость орбиты идеально постоянна, но обычно подвержена небольшим возмущениям, вызванным сжатием планет и присутствием других тел.

Положение космического корабля на орбите определяется истинной аномалией, $\nu$, угол, измеренный от периапсиса или для круговой орбиты от восходящего узла или опорного направления. Полуширокая прямая кишка , или лучевая кость под углом 90 градусов от периапсиса, это: $$p=a(1-e^{2})\,$$

Радиус в любом положении полета равен: $$r={\frac {p}{1+e\cos \nu }}$$и скорость в этом положении равна: $$v={\sqrt {\mu \left({\frac {2}{r}}-{\frac {1}{a}}\right)}}$$

Типы орбит

Круговой

Для круговой орбиты ra _: = r _p = a , а эксцентриситет равен 0. Круговая скорость на заданном радиусе равна $$v_{c}={\sqrt {\frac {\mu }{r}}}$$

Эллиптический

Для эллиптической орбиты e больше 0, но меньше 1. Перицентральная скорость равна: $$v_{p}={\sqrt {\frac {\mu (1+e)}{a(1-e)}}}$$а скорость апоапсиса равна: $$v_{a}={\sqrt {\frac {\mu (1-e)}{a(1+e)}}}\,$$

Предельным условием является параболическая орбита ухода , когда e = 1 и r _a становится бесконечным. Тогда скорость убегания в перицентре равна $$v_{e}={\sqrt {\frac {2\mu }{r_{p}}}}$$

Угол траектории полета

Удельный угловой момент любой конической орбиты h постоянен и равен произведению радиуса и скорости в перицентре. В любой другой точке орбиты оно равно: $$h=rv\cos \varphi ,$$где φ — угол траектории полета, отсчитываемый от местной горизонтали (перпендикулярно r ). Это позволяет рассчитать φ в любой точке орбиты, зная радиус и скорость: $$\varphi =\arccos \left({\frac {r_{p}v_{p}}{rv}}\right)$$

Обратите внимание, что угол траектории полета равен 0 градусам (90 градусов от местной вертикали) для круговой орбиты.

Истинная аномалия как функция времени

Можно показать, что приведенное выше уравнение углового момента также связывает скорость изменения истинной аномалии с r , v и φ , таким образом, истинная аномалия может быть найдена как функция времени с момента прохождения перицентра путем интегрирования: $$\nu =r_{p}v_{p}\int _{t_{p}}^{t}{\frac {1}{r^{2}}}\,dt$$

И наоборот, время, необходимое для достижения данной аномалии, равно: $$t={\frac {1}{r_{p}v_{p}}}\int _{0}^{\nu }r^{2}\,d\nu$$

Орбитальные маневры

Смотрите также: Орбитальный маневр

Находясь на орбите, космический корабль может запустить ракетные двигатели, чтобы перейти в плоскость на другую высоту или тип орбиты или изменить свою орбитальную плоскость. Эти маневры требуют изменения скорости корабля, и классическое уравнение ракеты используется для расчета потребности в топливе для заданной дельта-v . Бюджет дельта- v . суммирует все потребности в топливе или определяет общую дельта-v, доступную для заданного количества топлива для миссии Большинство маневров на орбите можно смоделировать как импульсивные , то есть как почти мгновенное изменение скорости с минимальной потерей точности.

Изменения в плоскости

Циркуляризация орбиты

Эллиптическую орбиту легче всего преобразовать в круговую орбиту в перицентре или апоцентре, применив одиночный запуск двигателя с дельтой v, равной разнице между желаемой круговой скоростью орбиты и скоростью перицентра или апоцентра текущей орбиты:

Для циркуляризации перицентра производят ретроградный ожог: $$\Delta v\ =v_{c}-v_{p}$$

Для циркуляризации при апоапсисе производят позиградный ожог: $$\Delta v\ =v_{c}-v_{a}$$

Изменение высоты за счет передачи Хомана

Переходная орбита Гомана, 2, с орбиты (1) на более высокую орбиту (3)

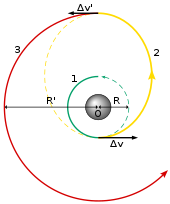
— Переходная орбита Гомана это простейший маневр, который можно использовать для перемещения космического корабля с одной высоты на другую. Требуются два запуска: первый для вывода корабля на эллиптическую переходную орбиту, а второй для превращения целевой орбиты в круговую.

Чтобы поднять круговую орбиту на $v_{1}$, первое положительное горение увеличивает скорость до перицентрической скорости переходной орбиты: $$\Delta v_{1}\ =v_{p}-v_{1}$$Второй позиградный ожог, сделанный в апоапсисе, повышает скорость до скорости целевой орбиты: $$\Delta v_{2}\ =v_{2}-v_{a}$$

Маневр снижения орбиты является зеркальным отражением маневра подъема; оба ожога сделаны ретроградными.

Изменение высоты за счет биэллиптического переноса

Биэллиптический переход с низкой круговой стартовой орбиты (темно-синий) на более высокую круговую орбиту (красный)

Несколько более сложный маневр изменения высоты — биэллиптический переход , состоящий из двух полуэллиптических орбит; первый, позиградный ожог отправляет космический корабль в произвольно высокое апоапсис, выбранное в какой-то момент. $r_{b}$ вдали от центрального тела. В этот момент второй запуск изменяет периапсис, чтобы он соответствовал радиусу последней желаемой орбиты, при этом выполняется третий, ретроградный запуск, чтобы вывести космический корабль на желаемую орбиту. Хотя это занимает больше времени для перевода, для биэллиптического перехода может потребоваться меньше топлива, чем для перевода Хомана, когда соотношение радиусов начальной и целевой орбиты составляет 12 или больше.

Ожог 1 (позиградный): $$\Delta v_{1}\ ={v_{p}}_{1}-v_{1}$$Запись 2 (позиградная или ретроградная), чтобы сопоставить перицентр с высотой целевой орбиты: $$\Delta v_{2}\ ={v_{a}}_{2}-{v_{a}}_{1}$$Ожог 3 (ретроградный): $$\Delta v_{3}\ =v_{2}-{v_{p}}_{2}$$

Смена самолета

Маневры смены самолета могут выполняться отдельно или в сочетании с другими корректировками орбиты. Для маневра чистого изменения плоскости вращения, состоящего только из изменения наклона орбиты, удельный угловой момент h начальной и конечной орбит равен по величине, но не по направлению. Следовательно, изменение удельного углового момента можно записать как: $$\Delta h=2h\sin \left({\frac {|\Delta i|}{2}}\right)$$где h - удельный угловой момент до смены плоскости, а Δ i - желаемое изменение угла наклона. Из этого можно показать что требуемая дельта- v равна: $$\Delta v={\frac {2h\sin {\frac {|\Delta i|}{2}}}{r}}$$

Из определения h это также можно записать как: $$\Delta v=2v\cos \varphi \sin \left({\frac {\left|\Delta i\right|}{2}}\right)$$где v — величина скорости до смены самолета, а φ — угол траектории полета. Используя приближение малого угла , это становится: $$\Delta v=v\cos(\varphi )\left|\Delta i\right|$$

Общая дельта- v для комбинированного маневра может быть рассчитана путем векторного сложения дельта- v чистого вращения и дельта- v для другого запланированного изменения орбиты.

Транслунный полет

Типичная транслунная траектория

Транспортные средства, отправляемые в лунные или планетарные миссии, обычно не запускаются путем непосредственного впрыска на траекторию вылета, а сначала выводятся на низкую околоземную парковочную орбиту ; это позволяет увеличить окно запуска и дать больше времени для проверки того, что транспортное средство находится в надлежащем состоянии для полета.

Для полета на Луну не требуется космическая скорость; Луны скорее, апогей транспортного средства поднят достаточно высоко, чтобы пройти через точку, в которой он входит в гравитационную сферу влияния (SOI). Это расстояние от спутника, на котором его гравитационное воздействие на космический корабль равно гравитационному притяжению его центрального тела, то есть $$r_{\text{SOI}}=D\left({\frac {m_{s}}{m_{c}}}\right)^{2/5},$$где D — среднее расстояние от спутника до центрального тела, а m _c и m _s — массы центрального тела и спутника соответственно. Это значение составляет примерно 66 300 километров (35 800 морских миль) от Луны.

Точное решение траектории требует рассмотрения как задачи трёх тел , но предварительную оценку можно сделать, используя исправленную коническую аппроксимацию орбит вокруг Земли и Луны, исправленную в точке SOI и принимая во внимание тот факт, что Луна вращающаяся система отсчета вокруг Земли.

Транслунная инъекция

Основная статья: Транслунная инъекция

Это должно быть рассчитано так, чтобы Луна оказалась в позиции для захвата транспортного средства, и в первом приближении это можно смоделировать как передачу Хомана. Однако продолжительность горения ракеты обычно достаточно велика и происходит при достаточном изменении угла траектории полета, что не очень точно. Его необходимо моделировать как неимпульсивный маневр , требующий интегрирования посредством анализа методом конечных элементов ускорений, вызванных движущей силой и силой тяжести, для получения скорости и угла траектории полета: $${\begin{aligned}{\dot {v}}&={\frac {F\cos \alpha }{m}}-g\cos \theta \\{\dot {\theta }}&={\frac {F\sin \alpha }{mv}}+\left({\frac {g}{v}}-{\frac {v}{r}}\right)\sin \theta ,\\v&=\int _{t_{0}}^{t}{\dot {v}}\,dt\\\theta &=\int _{t_{0}}^{t}{\dot {\theta }}\,dt\end{aligned}}$$где:

• F – тяга двигателя;
• α — угол атаки;
• m – масса автомобиля;
• r — радиальное расстояние до центра планеты; и
• g — гравитационное ускорение , которое изменяется обратно пропорционально квадрату радиального расстояния: $$g=g_{0}\left({\frac {r_{0}}{r}}\right)^{2}$$

Высота $h$, расстояние вниз $s$и радиальное расстояние $r$ от центра Земли тогда вычисляются как: $${\begin{aligned}h&=\int _{t_{0}}^{t}v\cos \theta \,dt\\r&=r_{0}+h\\s&=r_{0}\int _{t_{0}}^{t}{\frac {v}{r}}\sin \theta \,dt\end{aligned}}$$

Коррекции в середине курса

Простая лунная траектория остается в одной плоскости, что приводит к облету Луны или ее орбите в небольшом диапазоне наклона к экватору Луны. Это также допускает «свободное возвращение», при котором космический корабль вернется в подходящее положение для входа в атмосферу Земли, если бы он не был выведен на лунную орбиту. Для коррекции ошибок траектории обычно требуются относительно небольшие изменения скорости. Такая траектория использовалась для пилотируемых лунных миссий «Аполлон-8» , «Аполлон-10» , «Аполлон-11» и «Аполлон-12» .

Большую гибкость в покрытии лунной орбиты или посадочной площадки (при больших углах наклона Луны) можно получить, выполнив маневр смены самолета в середине полета; однако это исключает возможность свободного возврата, поскольку новый самолет уберет траекторию аварийного возвращения космического корабля в сторону от точки входа в атмосферу Земли и оставит космический корабль на высокой околоземной орбите. Этот тип траектории использовался в последних пяти миссиях Аполлона (с 13 по 17).

Вывод на лунную орбиту

В программе «Аполлон» выход на ретроградную лунную орбиту осуществлялся на высоте примерно 110 километров (59 морских миль) на обратной стороне Луны. Это стало перицинтионом начальных орбит с апоцинтионом порядка 300 километров (160 морских миль). Дельта v составляла примерно 1000 метров в секунду (3300 футов/с). Два витка спустя орбита стала круговой и составила 110 километров (59 морских миль). Для каждой миссии офицер по динамике полета готовил 10 вариантов вывода на лунную орбиту, чтобы можно было выбрать тот, который имеет оптимальный (минимальный) расход топлива и лучше всего соответствует требованиям миссии; это было загружено в компьютер космического корабля, и его должны были выполнять и контролировать астронавты на обратной стороне Луны, пока они были вне радиосвязи с Землей.

Межпланетный полет

Чтобы полностью покинуть гравитационное поле одной планеты и достичь другой, гиперболическая необходима траектория относительно исходной планеты с избыточной скоростью, добавленной к орбитальной скорости исходной планеты вокруг Солнца (или вычтенной из нее). Желаемая гелиоцентрическая переходная орбита к высшей планете будет иметь перигелий на исходной планете, что потребует приложения гиперболической избыточной скорости в положительном направлении, когда космический корабль находится вдали от Солнца. В на низшую планету пункте назначения афелий будет на планете вылета, а избыточная скорость применяется в ретроградном направлении, когда космический корабль движется к Солнцу. Для точных расчетов миссии элементы орбит планет должны быть получены из эфемерид . например, опубликованное Лабораторией реактивного движения НАСА .

Упрощение предположений

Тело	Эксцентриситет	Иметь в виду расстояние (10 6 км)	орбитальный скорость (км/сек)	орбитальный период (годы)	Масса Земля = 1	$\mu$ (км 3 /сек 2 )
Солнце	---	---	---	---	333,432	1.327 × 10 11
Меркурий	.2056	57.9	47.87	.241	.056	2.232 × 10 4
Венера	.0068	108.1	35.04	.615	.817	3.257 × 10 5
Земля	.0167	149.5	29.79	1.000	1.000	3.986 × 10 5
Марс	.0934	227.8	24.14	1.881	.108	4.305 × 10 4
Юпитер	.0484	778	13.06	11.86	318.0	1.268 × 10 8
Сатурн	.0541	1426	9.65	29.46	95.2	3.795 × 10 7
Уран	.0472	2868	6.80	84.01	14.6	5.820 × 10 6
Нептун	.0086	4494	5.49	164.8	17.3	6.896 × 10 6

В целях предварительного анализа миссии и технико-экономического обоснования можно сделать некоторые упрощенные предположения, позволяющие рассчитать дельту-v с очень небольшой ошибкой:

• Орбиты всех планет, за исключением Меркурия , имеют очень малый эксцентриситет, и поэтому их можно считать круговыми при постоянной орбитальной скорости и среднем расстоянии от Солнца.
• Орбиты всех планет (кроме Меркурия) почти компланарны, с очень небольшим наклоном к эклиптике (3,39 градуса и менее; наклонение Меркурия 7,00 градуса).
• Возмущающее воздействие гравитации других планет незначительно.
• Большую часть времени полета космический корабль проведет только под гравитационным воздействием Солнца, за исключением коротких периодов, когда он находится в сфере влияния планет отправления и назначения.

Поскольку межпланетные космические корабли проводят большой период времени на гелиоцентрической орбите между планетами, находящимися на относительно больших расстояниях друг от друга, приближение «патч-конус» гораздо точнее для межпланетных траекторий, чем для транслунных траекторий. Точка соединения между гиперболической траекторией относительно исходной планеты и гелиоцентрической переходной орбитой происходит в радиусе сферы влияния планеты относительно Солнца, как определено выше в разделе «Орбитальный полет» . Учитывая соотношение масс Солнца в 333 432 раза больше массы Земли и расстояние в 149 500 000 километров (80 700 000 морских миль), радиус сферы влияния Земли составляет 924 000 километров (499 000 морских миль) (примерно 1 000 000 километров).

Гелиоцентрическая переходная орбита

Переходная орбита, необходимая для перевода космического корабля с орбиты планеты вылета на планету назначения, выбирается из нескольких вариантов:

• требует Переходная орбита Гомана минимально возможного топлива и дельта-v; это половина эллиптической орбиты с афелием и перигелием, касательными к орбитам обеих планет, с самым длинным временем полета за пределы орбиты, равным половине периода эллипса. Это известно как миссия класса соединения . Варианта «свободного возвращения» нет, поскольку если космический корабль не выйдет на орбиту вокруг планеты назначения, а вместо этого завершит переходную орбиту, планета вылета не окажется в исходном положении. Использование другого трансфера Хомана для возвращения требует значительного времени ожидания на планете назначения, что приводит к очень длительному общему времени полета туда и обратно. Писатель-фантаст Артур Кларк в своей книге «Исследование космоса» 1951 года написал , что путешествие туда и обратно от Земли к Марсу потребует 259 дней в пути и еще 259 дней в пути, а также 425 дней пребывания на Марсе.
• Увеличение скорости апсиды вылета (и, следовательно, большой полуоси) приводит к тому, что траектория пересекает орбиту планеты назначения не касательно, прежде чем достичь противоположной апсиды, увеличивая дельту-v, но сокращая время исходящего транзита ниже максимального.
• маневр Гравитационный , иногда известный как «маневр с рогаткой» или миссия «Крокко» в честь ее предложившего в 1956 году Гаэтано Крокко , приводит к миссии оппозиционного класса с гораздо более коротким временем пребывания в пункте назначения. Это достигается путем пролета мимо другой планеты, используя ее гравитацию для изменения орбиты. Например, путешествие туда и обратно на Марс можно значительно сократить с 943 дней, необходимых для миссии по соединению, до менее года, если пролететь мимо Венеры по возвращении на Землю.

Гиперболический отъезд

Требуемая гиперболическая избыточная скорость v _∞ (иногда называемая характеристической скоростью ) представляет собой разницу между скоростью вылета переходной орбиты и гелиоцентрической орбитальной скоростью вылетающей планеты. Как только это будет определено, скорость впрыска относительно исходной планеты в перицентре составит: $$v_{p}={\sqrt {{\frac {2\mu }{r_{p}}}+v_{\infty }^{2}}}\,$$

Вектор избыточной скорости для гиперболы смещен от касательной перицентра на характерный угол, поэтому инжекционный ожог перицентра должен опережать точку вылета планеты на тот же угол: $$\delta =\arcsin {\frac {1}{e}}$$

Геометрическое уравнение эксцентриситета эллипса нельзя использовать для гиперболы. Но эксцентриситет можно рассчитать по динамическим формулировкам следующим образом: $$e={\sqrt {1+{\frac {2\varepsilon h^{2}}{\mu ^{2}}}}},$$где h - удельный угловой момент, указанный выше в разделе орбитального полета , рассчитанный в перицентре: $$h=r_{p}v_{p},$$ — ε удельная энергия: $$\varepsilon ={\frac {v^{2}}{2}}-{\frac {\mu }{r}}\,$$

Кроме того, уравнения для r и v, приведенные в «Орбитальном полете», зависят от большой полуоси и, следовательно, непригодны для траектории ухода. Но установив радиус в перицентре, равный уравнению r в нуле аномалия дает альтернативное выражение полурасширенной прямой кишки: $$p=r_{p}(1+e),\,$$что дает более общее уравнение радиуса и аномалии, которое можно использовать при любом эксцентриситете: $$r={\frac {r_{p}(1+e)}{1+e\cos \nu }}\,$$

Замена альтернативного выражения на p также дает альтернативное выражение для a (которое определено для гиперболы, но больше не представляет большую полуось). Это дает уравнение зависимости скорости от радиуса, которое также можно использовать при любом эксцентриситете: $$v={\sqrt {\mu \left({\frac {2}{r}}-{\frac {1-e^{2}}{r_{p}(1+e)}}\right)}}\,$$

Уравнения угла траектории полета и зависимости аномалии от времени, приведенные в разделе «Орбитальный полет», также можно использовать для гиперболических траекторий.

Запустить окна

Изменение скорости, необходимое для миссии, сильно варьируется во времени из-за постоянно меняющегося относительного положения планет. Поэтому оптимальные окна запуска часто выбираются по результатам графиков , показывающих контуры характеристической энергии ( v _∞ ² ) построено в зависимости от времени отправления и прибытия.

Вход в атмосферу

Основная статья: Вход в атмосферу

Контролируемый вход, спуск и приземление транспортного средства достигаются за счет сброса избыточной кинетической энергии за счет аэродинамического нагрева от сопротивления, что требует некоторых средств тепловой защиты и / или ретроградной тяги. Конечный спуск обычно достигается с помощью парашютов и/или воздушных тормозов .

Контроль отношения

Основная статья: Контроль отношения

Поскольку космические аппараты большую часть времени полета проводят в космическом вакууме без двигателя , они отличаются от самолетов тем, что траектория их полета не определяется их положением (ориентацией), за исключением полета в атмосфере для управления силами подъемной силы и сопротивления, а также во время полета в атмосфере. полет с приводом для выравнивания вектора тяги. Тем не менее, управление ориентацией часто поддерживается в полете без двигателя, чтобы удерживать космический корабль в фиксированной ориентации для целей астрономических наблюдений , связи или для солнечной энергии выработки ; или перевести его в контролируемое вращение для пассивного термоконтроля , или создать искусственную гравитацию внутри корабля.

Управление ориентацией осуществляется относительно инерциальной системы отсчета или другого объекта (небесной сферы, определенных полей, близлежащих объектов и т.п.). Положение корабля описывается углами относительно трех взаимно перпендикулярных осей вращения, называемых креном, тангажем и рысканием. Ориентация может быть определена путем калибровки с использованием внешней системы наведения, например, путем определения углов к опорной звезде или Солнцу, а затем внутреннего контроля с помощью инерциальной системы механических или оптических гироскопов . Ориентация — это векторная величина, описываемая тремя углами для мгновенного направления и мгновенными скоростями крена по всем трем осям вращения. Аспект управления подразумевает как осведомленность о мгновенной ориентации и скорости крена, так и способность изменять скорость крена для принятия новой ориентации с использованием либо системы управления реакцией , либо других средств.

Второй закон Ньютона, примененный к вращательному, а не к линейному движению, выглядит следующим образом: $${\boldsymbol {\tau }}_{x}=I_{x}{\boldsymbol {\alpha }}_{x},$$где ${\boldsymbol {\tau }}_{x}$ - чистый крутящий момент вокруг оси вращения, действующий на транспортное средство, I _x - его момент инерции относительно этой оси (физическое свойство, которое объединяет массу и ее распределение вокруг оси), и $\alpha _{x}$ — угловое ускорение вокруг этой оси в радианах в секунду в секунду. Следовательно, скорость ускорения в градусах в секунду за секунду равна $${\boldsymbol {\alpha }}_{x}={\tfrac {180}{\pi }}{\boldsymbol {\tau }}_{x}/I_{x},$$

Аналогично линейному движению, угловая скорость вращения ${\boldsymbol {\omega }}_{x}$ (градусов в секунду) получается путем интегрирования α по времени: $${\omega _{x}}=\int _{t_{0}}^{t}{\alpha _{x}}dt$$и угловое вращение ${\boldsymbol {\theta }}_{x}$ – интеграл скорости от скорости: $$\theta _{x}=\int _{t_{0}}^{t}{\omega _{x}}dt$$

Три основных момента инерции I _x , I _y и I _z относительно осей крена, тангажа и рыскания определяются через центр масс транспортного средства .

Управляющий крутящий момент ракеты-носителя иногда обеспечивается аэродинамически с помощью подвижных килей и обычно путем установки двигателей на подвесах для направления тяги вокруг центра масс. Крутящий момент часто прикладывается к космическому кораблю, работающему в отсутствие аэродинамических сил, с помощью системы управления реакцией - набора двигателей, расположенных вокруг корабля. Двигатели запускаются вручную или под автоматическим управлением короткими очередями для достижения желаемой скорости вращения, а затем запускаются в противоположном направлении, чтобы остановить вращение в желаемом положении. Крутящий момент вокруг определенной оси равен: $${\boldsymbol {\tau }}=\sum _{i=1}^{N}(\mathbf {r} _{i}\times \mathbf {F} _{i}),$$где r - его расстояние от центра масс, а F только составляющая F, перпендикулярная r - тяга отдельного двигателя ( включена ).

В ситуациях, когда расход топлива может быть проблемой (например, спутники длительного действия или космические станции), для обеспечения управляющего крутящего момента могут использоваться альтернативные средства, такие как реактивные колеса. или гироскопы управляющего момента .

Ссылки

• Андерсон, Джон Д. (2004), Введение в полет (5-е изд.), McGraw-Hill, ISBN  0-07-282569-3
• Бейт, Роджер Б.; Мюллер, Дональд Д.; Уайт, Джерри Э. (1971), Основы астродинамики , Дувр
• Пиво, Фердинанд П.; Джонстон, Рассел младший (1972), Векторная механика для инженеров: статика и динамика , McGraw-Hill
• Дрейк, Брет Г.; Бейкер, Джон Д.; Хоффман, Стефан Дж.; Ландау, Дэймон; Воулс, Стивен А. (2017). «Варианты траектории исследования Марса и спутников Марса». Группа НАСА по архитектуре пилотируемых космических полетов (презентация) .
• Фелленц, Д.В. (1967). «Вход в атмосферу». У Теодора Баумайстера (ред.). Стандартный справочник Маркса для инженеров-механиков (Седьмое изд.). Нью-Йорк: Макгроу Хилл. стр. 11: 155–58. ISBN  0-07-142867-4 .
• Гласстоун, Сэмюэл (1965). Справочник по космическим наукам . Компания Д. Ван Ностранд, Инк.
• Хинц, Джеральд Р. (2015). Орбитальная механика и астродинамика: методы и инструменты космических полетов . Чам. ISBN  978-3-319-09444-1 . OCLC   900730410 . {{cite book}}: CS1 maint: отсутствует местоположение издателя ( ссылка )
• Кромис, AJ (1967). «Анализ траектории полета с двигателем». У Теодора Баумайстера (ред.). Стандартный справочник Маркса для инженеров-механиков (Седьмое изд.). Нью-Йорк: Макгроу Хилл. стр. 11: 154–55. ISBN  0-07-142867-4 .
• Мэттфельд, Брайан; Стромгрен, Чел; Шайфейс, Хилари; Комар, Дэвид Р.; Чирилло, Уильям; Гудлифф, Кандис (2015). Обмен траекториями классов оппозиции и соединения для ранних миссий человека на Марс (PDF) (Отчет) . Проверено 10 июля 2018 г.
• Перри, WR (1967). «Орбитальная механика». У Теодора Баумайстера (ред.). Стандартный справочник Маркса для инженеров-механиков (Седьмое изд.). Нью-Йорк: Макгроу Хилл. стр. 11: 151–52. ISBN  0-07-142867-4 .
• Рассел, JW (1967). «Механика лунного и межпланетного полета». У Теодора Баумайстера (ред.). Стандартный справочник Маркса для инженеров-механиков (Седьмое изд.). Нью-Йорк: МакГроу-Хилл. стр. 11: 152–54. ISBN  0-07-142867-4 .
• Сиди, М.Дж. «Динамика и управление космическим кораблем. Кембридж, 1997.
• Томсон, В.Т. «Введение в космическую динамику». Дувр, 1961 год.
• Вертц, младший «Определение ориентации космического корабля и управление им». Клювер, 1978.
• Визель, М.Е. «Динамика космического полета». МакГроу-Хилл, 1997.