Переходная орбита Гомана

В космонавтике переходная орбита Гомана ( / ˈ h oʊ m ə n / ) — орбитальный маневр , используемый для перевода космического корабля между двумя орбитами разной высоты вокруг центрального тела. Например, передача Хомана может быть использована для перевода орбиты спутника с низкой околоземной орбиты на геостационарную орбиту . В идеализированном случае начальная и целевая орбиты одновременно круговые и компланарные . Маневр осуществляется путем вывода корабля на эллиптическую переходную орбиту , касательную как к начальной, так и к целевой орбитам. В маневре используются два импульсных включения двигателя: первый устанавливает переходную орбиту, а второй корректирует орбиту в соответствии с целью.

Маневр Гомана часто использует минимально возможную величину импульса (которая потребляет пропорциональное количество дельта-v и, следовательно, топлива ) для выполнения передачи, но требует относительно большего времени перемещения, чем передачи с более высоким импульсом. В некоторых случаях, когда одна орбита намного больше другой, биэллиптический переход может использовать даже меньший импульс за счет еще большего времени полета.

Маневр был назван в честь Вальтера Гомана , немецкого учёного, опубликовавшего его описание в своей книге 1925 года Die Erreichbarkeit der Himmelskörper ( «Достижимость небесных тел »). ^[1] Частично на Хомана повлиял немецкий писатель-фантаст Курд Лассвиц и его книга 1897 года « Две планеты» .

При использовании для путешествий между небесными телами переходная орбита Гомана требует, чтобы начальная и конечная точки находились в определенных местах на их орбитах относительно друг друга. Космические миссии, использующие трансфер Хомана, должны дождаться выполнения этого необходимого выравнивания, что открывает окно запуска . для миссии между Землей и Марсом Например, эти окна запуска происходят каждые 26 месяцев. Переходная орбита Хомана также определяет фиксированное время, необходимое для перемещения между начальной точкой и точкой назначения; для путешествия Земля-Марс это время в пути составляет около 9 месяцев. Когда переход осуществляется между орбитами, близкими к небесным телам со значительной гравитацией, гораздо меньше дельта-v обычно требуется эффект Оберта , поскольку для ожогов может использоваться .

Они также часто используются в таких ситуациях, но низкоэнергетические передачи , которые учитывают ограничения тяги реальных двигателей и используют гравитационные колодцы обеих планет, могут быть более экономичными. ^[2]^[3]^[4]

Пример

На схеме изображена переходная орбита Гомана для вывода космического корабля с нижней круговой орбиты на более высокую. Это эллиптическая орбита , касательная как к нижней круговой орбите, которую должен покинуть космический корабль (голубая, обозначена цифрой 1 на схеме), так и к более высокой круговой орбите, которой он должен достичь (красная, обозначена цифрой 3 на схеме). Переходная орбита (желтая, обозначена цифрой 2 на схеме) инициируется запуском двигателя космического корабля для добавления энергии и поднятия апогея . Когда космический корабль достигает апогея, запуск второго двигателя добавляет энергии, чтобы поднять перигей, выводя космический корабль на большую круговую орбиту.

Благодаря обратимости орбит подобная переходная орбита Гомана может использоваться для перевода космического корабля с более высокой орбиты на более низкую; в этом случае двигатель космического корабля запускается в направлении, противоположном его текущему пути, замедляя космический корабль и опуская его перигей до перигея эллиптической переходной орбиты. Затем двигатель снова запускается на меньшем расстоянии, чтобы вывести космический корабль на нижнюю круговую орбиту. Трансферная орбита Гомана основана на двух мгновенных изменениях скорости . Требуется дополнительное топливо, чтобы компенсировать тот факт, что всплески требуют времени; это сводится к минимуму за счет использования двигателей большой тяги для минимизации продолжительности всплесков. При полетах на околоземную орбиту эти два ожога обозначаются как перигейный ожог и апогейный ожог (или удар апогея) . ^[5]); в более общем смысле их называют перицентра и апоапсиса ожогами . Альтернативно, второй цикл для формирования круговой орбиты может называться циклическим циклическим циклом .

Тип I и Тип II

Идеальная переходная орбита Гомана переходит между двумя круговыми орбитами в одной плоскости и проходит ровно на 180 ° вокруг главной. В реальном мире орбита назначения может быть не круговой и не компланарной начальной орбите. Реальные переходные орбиты могут проходить немного больше или немного меньше 180 ° вокруг главной звезды. Орбита, которая проходит менее 180 ° вокруг первичной обмотки, называется передачей Гомана «Типа I», а орбита, которая проходит более чем на 180 °, называется передачей Гомана «Типа II». ^[6]^[7]

Переходные орбиты могут поворачиваться вокруг главной звезды более чем на 360°. Эти многооборотные передачи иногда называют Типом III и Типом IV, где Тип III — это Тип I плюс 360°, а Тип IV — это Тип II плюс 360°. ^[8]

Использование

Переходная орбита Гомана может использоваться для перевода орбиты объекта к другому объекту, если они вращаются по совместной орбите более массивного тела. В контексте Земли и Солнечной системы сюда входит любой объект, вращающийся вокруг Солнца . Примером использования переходной орбиты Гомана является контакт астероида, вращающегося вокруг Солнца, с Землей. ^[9]

Расчет

Для небольшого тела, вращающегося вокруг другого, гораздо большего тела, такого как спутник, вращающийся вокруг Земли, полная энергия меньшего тела равна сумме его кинетической энергии и потенциальной энергии , и эта полная энергия также равна половине потенциала на орбите Земли. среднее расстояние $a$ ( большая полуось ): $E={\frac {mv^{2}}{2}}-{\frac {GMm}{r}}={\frac {-GMm}{2a}}.$

Решение этого уравнения для скорости приводит к уравнению vis-viva : $v^{2}=\mu \left({\frac {2}{r}}-{\frac {1}{a}}\right),$ где:

$v$ - скорость вращающегося тела,
$\mu =GM$ — стандартный гравитационный параметр первичного тела, предполагая $M+m$ не значительно больше, чем $M$ (что делает $v_{M}\ll v$ ), (для Земли это μ ~3.986E14 м ³ с ⁻²)
$r$ - расстояние вращающегося тела от главного фокуса,
$a$ — большая полуось орбиты тела.

Следовательно, дельта- v (Δv), необходимая для передачи Гомана, может быть вычислена следующим образом в предположении мгновенных импульсов: $\Delta v_{1}={\sqrt {\frac {\mu }{r_{1}}}}\left({\sqrt {\frac {2r_{2}}{r_{1}+r_{2}}}}-1\right),$ выйти на эллиптическую орбиту в $r=r_{1}$ из $r_{1}$ круговая орбита, где $r_{2}$ - афелий полученной эллиптической орбиты, а $\Delta v_{2}={\sqrt {\frac {\mu }{r_{2}}}}\left(1-{\sqrt {\frac {2r_{1}}{r_{1}+r_{2}}}}\right),$ покинуть эллиптическую орбиту в $r=r_{2}$ к $r_{2}$ круговая орбита,где $r_{1}$ и $r_{2}$ – соответственно радиусы круговых орбит вылета и прибытия; меньший (больший) из $r_{1}$ и $r_{2}$ соответствует расстоянию перицентра ( расстоянию апоцентра ) эллиптической передаточной орбиты Гомана. Обычно $\mu$ дается в единицах м ³/с ², поэтому обязательно используйте метры, а не километры, для $r_{1}$ и $r_{2}$ . Всего $\Delta v$ тогда:

$\Delta v_{\text{total}}=\Delta v_{1}+\Delta v_{2}.$

Независимо от того, переходите ли вы на более высокую или низкую орбиту, согласно третьему закону Кеплера , время, необходимое для перехода между орбитами, равно

$t_{\text{H}}={\frac {1}{2}}{\sqrt {\frac {4\pi ^{2}a_{\text{H}}^{3}}{\mu }}}=\pi {\sqrt {\frac {(r_{1}+r_{2})^{3}}{8\mu }}}$ (половина периода обращения всего эллипса), где $a_{\text{H}}$ — длина большой полуоси передаточной орбиты Гомана.

Применительно к путешествию от одного небесного тела к другому крайне важно начинать маневр в тот момент, когда два тела выровнены должным образом. Учитывая, что угловая скорость цели $\omega _{2}={\sqrt {\frac {\mu }{r_{2}^{3}}}},$ угловое выравнивание α (в радианах ) во время начала между исходным объектом и целевым объектом должно быть $\alpha =\pi -\omega _{2}t_{\text{H}}=\pi \left(1-{\frac {1}{2{\sqrt {2}}}}{\sqrt {\left({\frac {r_{1}}{r_{2}}}+1\right)^{3}}}\right).$

Пример

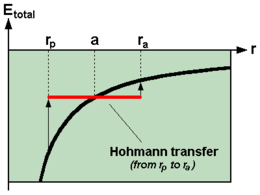
Рассмотрим геостационарную переходную орбиту , начинающуюся с r ₁ = 6678 км (высота 300 км) и заканчивающуюся геостационарной орбитой с r ₂ = 42 164 км (высота 35 786 км).

На меньшей круговой орбите скорость составляет 7,73 км/с; в большем - 3,07 км/с. На эллиптической орбите между ними скорость изменяется от 10,15 км/с в перигее до 1,61 км/с в апогее.

Следовательно, Δv для первого сжигания составляет 10,15–7,73 = 2,42 км/с, для второго сжигания 3,07–1,61 = 1,46 км/с, а для обоих вместе 3,88 км/с.

Это больше , чем Δv, необходимое для убегающей орбиты : 10,93–7,73 = 3,20 км/с. Применение Δv на низкой околоземной орбите (НОО) всего на 0,78 км/с больше (3,20–2,42) дало бы ракете скорость убегания , которая меньше, чем Δv 1,46 км/с, необходимая для круговой геостационарной орбиты. Это иллюстрирует эффект Оберта , заключающийся в том, что на больших скоростях одно и то же Δv обеспечивает более удельную орбитальную энергию , а увеличение энергии максимизируется, если человек тратит Δv как можно быстрее, а не тратит ее часть на замедление под действием силы тяжести, а затем тратит еще немного на преодоление замедление (конечно, цель переходной орбиты Гомана другая).

В худшем случае максимальная дельта- v

Как показывает приведенный выше пример, Δ v, необходимое для выполнения перехода Хомана между двумя круговыми орбитами, не является самым большим, когда радиус пункта назначения бесконечен. (Скорость убегания в √ 2 раза превышает орбитальную скорость, поэтому Δv, необходимое для убегания, составляет √ 2 - 1 (41,4%) от орбитальной скорости.) Требуемое Δv является наибольшим (53,0% от меньшей орбитальной скорости), когда радиус большего орбита в 15,5817... раз больше меньшей орбиты. ^[10] Это число является положительным корнем из $x 3 - 15 х 2 - 9 x - 1 = 0$ , что ${\textstyle 5+4\,{\sqrt {7}}\cos \left({1 \over 3}\arctan {{\sqrt {3}} \over 37}\right)}$ . Для более высоких соотношений орбит $Δ v,$ необходимое для второго сгорания, уменьшается быстрее, чем увеличивается первое.

Заявка на межпланетное путешествие

При использовании для перемещения космического корабля с орбиты одной планеты на орбиту другой эффект Оберта позволяет использовать меньшее значение дельта- v , чем сумма дельта- v, для отдельных маневров по уходу от первой планеты с последующим переходом Хомана на вторую планету. с последующим выходом на орбиту вокруг другой планеты.

Например, рассмотрим космический корабль, путешествующий с Земли на Марс . В начале своего путешествия космический корабль уже будет иметь определенную скорость и кинетическую энергию, связанную с его орбитой вокруг Земли. Во время горения ракетный двигатель применяет свою дельта- v , но кинетическая энергия увеличивается по квадратичному закону, пока ее не становится достаточно, чтобы преодолеть гравитационный потенциал планеты , а затем сгорает еще больше, чтобы получить достаточно энергии для перехода на переходную орбиту Гомана. (вокруг Солнца ). Поскольку ракетный двигатель способен использовать начальную кинетическую энергию топлива, требуется гораздо меньшая дельта- v сверх той, которая необходима для достижения скорости убегания, и оптимальной ситуацией является ситуация, когда переходное горение производится на минимальной высоте ( низкий периапсис ) над планетой. Требуемая дельта- v составляет всего 3,6 км/с, что всего примерно на 0,4 км/с больше, чем необходимо для отрыва от Земли, даже несмотря на то, что в результате космический корабль будет двигаться на 2,9 км/с быстрее Земли, направляясь к Марсу (см. таблицу ниже).

На другом конце космический корабль должен замедлиться, чтобы гравитация Марса захватила его. Это захватное сжигание лучше всего проводить на малой высоте, чтобы наилучшим образом использовать эффект Оберта. Следовательно, для организации передачи необходимы относительно небольшие тяги на обоих концах пути по сравнению с ситуацией в свободном пространстве.

Однако при любом перемещении Хомана решающее значение имеет выравнивание двух планет на их орбитах: планета назначения и космический корабль должны одновременно прибыть в одну и ту же точку на своих орбитах вокруг Солнца. Это требование согласованности порождает концепцию окон запуска .

Термин «лунная переходная орбита» (LTO) используется для обозначения Луны .

Можно применить приведенную выше формулу для расчета Δv в км/с, необходимого для выхода на переходную орбиту Гомана для прибытия в различные пункты назначения с Земли (при условии круговых орбит планет). В этой таблице столбец с надписью «Δv для выхода на орбиту Гомана с орбиты Земли» показывает изменение скорости Земли на скорость, необходимую для попадания на эллипс Гомана, другой конец которого будет находиться на желаемом расстоянии от Солнца. В столбце с надписью «Высота НОО» указана необходимая скорость (в невращающейся системе отсчета с центром на Земле) на высоте 300 км над поверхностью Земли. Это получается добавлением к удельной кинетической энергии квадрата скорости убегания (10,9 км/с) с этой высоты. Столбец «НОО» — это просто предыдущая скорость минус орбитальная скорость НОО, равная 7,73 км/с.

Место назначения	орбитальный радиус ( В )	Δ v (км/с) для выхода на орбиту Гомана из
Место назначения	орбитальный радиус ( В )	Орбита Земли	Высота Льва	ЛЕО
Солнце	0	29.8	31.7	24.0
Меркурий	0.39	7.5	13.3	5.5
Венера	0.72	2.5	11.2	3.5
Марс	1.52	2.9	11.3	3.6
Юпитер	5.2	8.8	14.0	6.3
Сатурн	9.54	10.3	15.0	7.3
Уран	19.19	11.3	15.7	8.0
Нептун	30.07	11.7	16.0	8.2
Плутон	39.48	11.8	16.1	8.4
Бесконечность	∞	12.3	16.5	8.8

Обратите внимание, что в большинстве случаев Δ v с НОО меньше, чем Δ v для выхода на орбиту Гомана с орбиты Земли.

Чтобы добраться до Солнца, на самом деле не обязательно использовать Δ v, равную 24 км/с. Можно использовать скорость 8,8 км/с, чтобы уйти очень далеко от Солнца, затем использовать ничтожное значение Δ v, чтобы довести угловой момент до нуля, а затем упасть на Солнце. Это можно рассматривать как последовательность двух передач Хомана: вверх и вниз. Кроме того, в таблице не указаны значения, которые применялись бы при использовании Луны в качестве гравитационной помощи . Существуют также возможности использования одной планеты, например Венеры, до которой легче всего добраться, для достижения других планет или Солнца.

Сравнение с другими трансферами

Биэллиптическая передача

Биэллиптический переход состоит из двух полуэллиптических орбит . С начальной орбиты первый запуск расходует дельта-v для вывода космического корабля на первую переходную орбиту с апоапсисом в какой-то момент. $r_{b}$ вдали от центрального тела . В этот момент второй запуск отправляет космический корабль на вторую эллиптическую орбиту с перицентром радиуса последней желаемой орбиты, где выполняется третий запуск, выводящий космический корабль на желаемую орбиту. ^[11]

Хотя они требуют на один запуск двигателя больше, чем передача Гомана, и, как правило, требуют большего времени в пути, некоторые биэллиптические передачи требуют меньшего количества общего дельта-v, чем передача Гомана, когда отношение конечной и начальной большой полуосей составляет 11,94. или больше, в зависимости от выбранной промежуточной большой полуоси. ^[12]

Впервые возникла идея биэллиптической траектории переноса. ^{[ нужна ссылка ]} опубликовано Ари Штернфельдом в 1934 году. ^[13]

Передача с низкой тягой

Двигатели малой тяги могут приближаться к переходной орбите Гомана, создавая постепенное увеличение начальной круговой орбиты за счет тщательно рассчитанных запусков двигателей. Для этого требуется изменение скорости (delta- v ) , большее, чем двухимпульсная передаточная орбита. ^[14] и выполнение занимает больше времени.

Такие двигатели, как ионные двигатели, сложнее анализировать с помощью модели delta- v . Эти двигатели имеют очень низкую тягу и в то же время гораздо более высокий дельта- V , гораздо более высокий удельный импульс , меньшую массу топлива и двигателя. Маневр переноса Хомана с двумя включениями был бы непрактичным при такой низкой тяге; маневр в основном оптимизирует использование топлива, но в данной ситуации его относительно много.

Если в ходе миссии планируются только маневры с малой тягой, то непрерывная работа двигателя с низкой тягой, но с очень высоким КПД может генерировать более высокую дельта- v и в то же время использовать меньше топлива, чем обычный химический ракетный двигатель.

Переход с одной круговой орбиты на другую путем постепенного изменения радиуса просто требует той же дельты, что и разница между двумя скоростями. ^[14] Такой маневр требует большей дельты, чем маневр Хомана с двумя включениями, но он выполняется с постоянной низкой тягой, а не с кратковременными применениями высокой тяги.

Количество используемой массы топлива измеряет эффективность маневра плюс используемое для него оборудование. Используемая общая дельта- v измеряет только эффективность маневра. Для электрических двигательных установок, которые, как правило, имеют малую тягу, высокая эффективность двигательной системы обычно компенсирует более высокое значение дельта-V по сравнению с более эффективным маневром Хомана.

Переходные орбиты с использованием электрических силовых установок или двигателей малой тяги оптимизируют время перехода для достижения конечной орбиты, а не дельта-v, как на переходной орбите Хомана. Для геостационарной орбиты исходная орбита устанавливается как суперсинхронная, и за счет непрерывного воздействия в направлении скорости в апогее переходная орбита преобразуется в круговую геостационарную. Однако этот метод требует гораздо больше времени из-за низкой тяги, выводимой на орбиту. ^[15]

Межпланетная транспортная сеть

В 1997 году был опубликован набор орбит, известный как Межпланетная транспортная сеть (ITN), обеспечивающий еще более низкие дельта- V (хотя и гораздо более медленные и длинные) пути между различными орбитами, чем переходные орбиты Гомана. ^[16] Межпланетная транспортная сеть по своей природе отличается от передач Хомана, поскольку перевозки Хомана предполагают только одно большое тело, а Межпланетная транспортная сеть - нет. Межпланетная транспортная сеть способна добиться использования менее движущей силы дельта- вращения за счет использования гравитационной помощи планет. ^{[ нужна ссылка ]}

См. также

Цитаты

^ Уолтер Хоманн, Достижимость небесных тел (Вашингтон: Технический перевод НАСА F-44, 1960) Интернет-архив .
^ Уильямс, Мэтт (26 декабря 2014 г.). «Сделать путешествие на Марс дешевле и проще: аргументы в пользу баллистического захвата» . Вселенная сегодня . Проверено 29 июля 2019 г.
^ Хадхази, Адам. «Новый способ добраться до Марса безопасно, в любое время и недорого» . Научный американец . Проверено 29 июля 2019 г.
^ «Введение в Берешит и его траекторию на Луну» . Гереши . 08.04.2019 . Проверено 29 июля 2019 г.
^ Джонатан Макдауэлл, « Удар в апогей: 40 лет применения верхних ступеней твердотопливных ракетных двигателей, 1957–1997 », 33-я конференция AIAA по совместным двигателям, 4 июля 1997 г. , аннотация . Проверено 18 июля 2017 г.
^ НАСА, Основы космических полетов , Раздел 1, Глава 4, « Траектории ». Проверено 26 июля 2017 г. Также доступен spaceodyssey.dmns.org .
^ Тайсон Спаркс, Траектории к Марсу. Архивировано 28 октября 2017 г. в Wayback Machine , Центр астродинамических исследований Колорадо, 14 декабря 2012 г. Проверено 25 июля 2017 г.
^ Ланжевен, Ю. (2005). «Проблемы проектирования космических научных миссий», Полезная нагрузка и определение миссий в космических науках , В. Мартинес Пилле, А. Апарисио и Ф. Санчес, ред., Cambridge University Press, стр. 30. ISBN 052185802X , 9780521858021
^ Калла, Пабло; Фрис, Дэн; Уэлч, Крис (2018). «Добыча астероидов с помощью малых космических аппаратов и ее экономическая целесообразность». arXiv : 1808.05099 [ astro-ph.IM ].
^ Валладо, Дэвид Энтони (2001). Основы астродинамики и приложения . Спрингер. п. 317. ИСБН 0-7923-6903-3 .
^ Кертис, Ховард (2005). Орбитальная механика для студентов-инженеров . Эльзевир . п. 264. ИСБН 0-7506-6169-0 .
^ Валладо, Дэвид Энтони (2001). Основы астродинамики и приложения . Спрингер. п. 318. ИСБН 0-7923-6903-3 .
^ Штернфельд, Ари Дж. (12 февраля 1934 г.), приближения к центральному притягивающему телу с заданной «О разрешенных траекториях кеплеровской орбиты», Отчеты Академии наук (на французском языке), 198 (1), Париж: 711. –713 .
^ Jump up to: ^а ^б Массачусетский технологический институт, 16.522: Космическое движение , сессия 6, « Аналитические аппроксимации для маневров с малой тягой », весна 2015 г. (получено 26 июля 2017 г.)
^ Спитцер, Арнон (1997). Оптимальная траектория переходной орбиты с использованием электродвижения . ВПТЗ США .
^ Ло, МВт ; Росс, SD (1997). «Серфинг по Солнечной системе: инвариантные многообразия и динамика Солнечной системы» . Технический отчет . МОМ. Лаборатория реактивного движения . стр. 2–4. 312/97.

Общие и цитируемые источники

Бейт, РР; Мюллер, Д.Д.; Уайт, Дж. Э. (1971). Основы астродинамики . Нью-Йорк: Dover Publications. ISBN 978-0-486-60061-1 .
Баттин, Р.Х. (1999). Введение в математику и методы астродинамики . Вашингтон, округ Колумбия: Американский институт аэронавтики и Ast. ISBN 978-1-56347-342-5 .
Хоманн, Вальтер (1925). Доступность небесных тел . Мюнхен: Р. Ольденбург Верлаг. ISBN 3-486-23106-5 .
Торнтон, Стивен Т.; Мэрион, Джерри Б. (2003). Классическая динамика частиц и систем (5-е изд.). Брукс Коул . ISBN 0-534-40896-6 .
Валладо, Д.А. (2001). Основы астродинамики и приложений (2-е изд.). Спрингер. ISBN 978-0-7923-6903-5 .

Дальнейшее чтение

«Орбитальная механика» . Ракетно-космическая техника . Роберт А. Бреуниг. Архивировано из оригинала 4 февраля 2012 г. Проверено 17 августа 2005 г.
«4. Межпланетные траектории» . Основы космического полета . Лаборатория реактивного движения: НАСА .

[1] Уолтер Хоманн, Достижимость небесных тел (Вашингтон: Технический перевод НАСА F-44, 1960) Интернет-архив .

[2] Уильямс, Мэтт (26 декабря 2014 г.). «Сделать путешествие на Марс дешевле и проще: аргументы в пользу баллистического захвата» . Вселенная сегодня . Проверено 29 июля 2019 г.

[3] Хадхази, Адам. «Новый способ добраться до Марса безопасно, в любое время и недорого» . Научный американец . Проверено 29 июля 2019 г.

[4] «Введение в Берешит и его траекторию на Луну» . Гереши . 08.04.2019 . Проверено 29 июля 2019 г.

[5] Джонатан Макдауэлл, « Удар в апогей: 40 лет применения верхних ступеней твердотопливных ракетных двигателей, 1957–1997 », 33-я конференция AIAA по совместным двигателям, 4 июля 1997 г. , аннотация . Проверено 18 июля 2017 г.

[NASA-trajectories-6] НАСА, Основы космических полетов , Раздел 1, Глава 4, « Траектории ». Проверено 26 июля 2017 г. Также доступен spaceodyssey.dmns.org .

[7] Тайсон Спаркс, Траектории к Марсу. Архивировано 28 октября 2017 г. в Wayback Machine , Центр астродинамических исследований Колорадо, 14 декабря 2012 г. Проверено 25 июля 2017 г.

[8] Ланжевен, Ю. (2005). «Проблемы проектирования космических научных миссий», Полезная нагрузка и определение миссий в космических науках , В. Мартинес Пилле, А. Апарисио и Ф. Санчес, ред., Cambridge University Press, стр. 30. ISBN 052185802X , 9780521858021

[9] Калла, Пабло; Фрис, Дэн; Уэлч, Крис (2018). «Добыча астероидов с помощью малых космических аппаратов и ее экономическая целесообразность». arXiv : 1808.05099 [ astro-ph.IM ].

[10] Валладо, Дэвид Энтони (2001). Основы астродинамики и приложения . Спрингер. п. 317. ИСБН 0-7923-6903-3 .

[Curtis-11] Кертис, Ховард (2005). Орбитальная механика для студентов-инженеров . Эльзевир . п. 264. ИСБН 0-7506-6169-0 .

[Vallado-12] Валладо, Дэвид Энтони (2001). Основы астродинамики и приложения . Спрингер. п. 318. ИСБН 0-7923-6903-3 .

[sternfeld1934-13] Штернфельд, Ари Дж. (12 февраля 1934 г.), приближения к центральному притягивающему телу с заданной «О разрешенных траекториях кеплеровской орбиты», Отчеты Академии наук (на французском языке), 198 (1), Париж: 711. –713 .

[MIT_16.522-14] Jump up to: ^а ^б Массачусетский технологический институт, 16.522: Космическое движение , сессия 6, « Аналитические аппроксимации для маневров с малой тягой », весна 2015 г. (получено 26 июля 2017 г.)

[15] Спитцер, Арнон (1997). Оптимальная траектория переходной орбиты с использованием электродвижения . ВПТЗ США .

[16] Ло, МВт ; Росс, SD (1997). «Серфинг по Солнечной системе: инвариантные многообразия и динамика Солнечной системы» . Технический отчет . МОМ. Лаборатория реактивного движения . стр. 2–4. 312/97.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]