Коническая постоянная

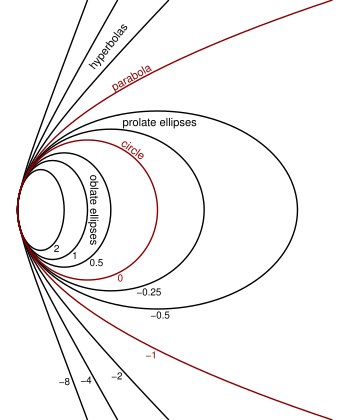
В геометрии коническая постоянная (или постоянная Шварцшильда , ^[1] по Карлу Шварцшильду ) — величина, описывающая сечения , и обозначается буквой К. конические Константа определяется выражением $K=-e^{2},$ где $е$ — эксцентриситет конического сечения.

Уравнение конического сечения с вершиной в начале координат и касательной к оси y: $y^{2}-2Rx+(K+1)x^{2}=0$ попеременно $x={\dfrac {y^{2}}{R+{\sqrt {R^{2}-(K+1)y^{2}}}}}$ где R — радиус кривизны при $x = 0$ .

Эта формулировка используется в геометрической оптике для определения сплюснутого эллиптического ( $K > 0$ ), сферического ( $K = 0$ ), вытянутого эллиптического ( $0 > K > -1$ ), параболического ( $K = -1$ ) и гиперболического ( $K < -1)$ ) поверхности линз и зеркал. Когда параксиальное приближение справедливо, оптическую поверхность можно рассматривать как сферическую поверхность с тем же радиусом.

Ссылки

^ Ракич, Андрей (18 августа 2005 г.). Сасиан, Хосе М; Кошель, Р. Джон; Юргенс, Ричард С. (ред.). «100-летие со дня рождения конической постоянной и революционных работ Шварцшильда в оптике» . Проектирование и оптимизация новых оптических систем VIII . 5875 . Международное общество оптики и фотоники: 587501. Бибкод : 2005SPIE.5875....1R . дои : 10.1117/12.635041 . S2CID 119718303 .

Смит, Уоррен Дж. (2008). Современная оптическая техника, 4-е изд . МакГроу-Хилл Профессионал . стр. 512–515. ISBN 978-0-07-147687-4 .

Эта посвященная геометрии, статья, незавершена . Вы можете помочь Википедии, расширив ее .

[1] Ракич, Андрей (18 августа 2005 г.). Сасиан, Хосе М; Кошель, Р. Джон; Юргенс, Ричард С. (ред.). «100-летие со дня рождения конической постоянной и революционных работ Шварцшильда в оптике» . Проектирование и оптимизация новых оптических систем VIII . 5875 . Международное общество оптики и фотоники: 587501. Бибкод : 2005SPIE.5875....1R . дои : 10.1117/12.635041 . S2CID 119718303 .

[1]