Эллиптический интеграл

В интегральном исчислении эллиптический интеграл — это одна из ряда связанных функций, определяемых как значение некоторых интегралов, которые были впервые изучены Джулио Фаньяно и Леонардом Эйлером ( ок. 1750 ). задачей нахождения длины дуги эллипса Их название происходит от их первоначального возникновения в связи с .

Современная математика определяет «эллиптический интеграл» как любую функцию f , которую можно выразить в форме

$$f(x)=\int _{c}^{x}R{\left({\textstyle t,{\sqrt {P(t)}}}\right)}\,dt,$$

где R — рациональная функция двух своих аргументов, P — многочлен степени 3 или 4 без повторяющихся корней, а c — константа.

Вообще говоря, интегралы в таком виде не могут быть выражены через элементарные функции . Исключениями из этого общего правила являются случаи, когда P имеет повторяющиеся корни, или когда R ( x , y ) не содержит нечетных степеней y , или если интеграл псевдоэллиптический. Однако с помощью соответствующей формулы приведения каждый эллиптический интеграл можно привести к форме, включающей интегралы по рациональным функциям и трем каноническим формам Лежандра (т. е. эллиптическим интегралам первого, второго и третьего рода).

Помимо формы Лежандра, приведенной ниже, эллиптические интегралы также могут быть выражены в симметричной форме Карлсона . Дополнительное понимание теории эллиптического интеграла можно получить путем изучения отображения Шварца – Кристоффеля . Исторически эллиптические функции были открыты как обратные функции эллиптических интегралов.

Обозначение аргумента

Неполные эллиптические интегралы являются функциями двух аргументов; полные эллиптические интегралы являются функциями одного аргумента. Эти аргументы выражаются множеством разных, но эквивалентных способов (они дают один и тот же эллиптический интеграл). Большинство текстов придерживаются канонической схемы именования, используя следующие соглашения об именах.

Для выражения одного аргумента:

• α , модульный угол
• k = sin α , эллиптический модуль или эксцентриситет
• м = к ² = грех ² α , параметр

Каждая из трех вышеуказанных величин полностью определяется любой из остальных (при условии, что они неотрицательны). Таким образом, их можно использовать взаимозаменяемо.

Другой аргумент также может быть выражен как φ , амплитуда , или как x или u , где x = sin φ = sn u и sn — одна из эллиптических функций Якоби .

Указание значения любой из этих величин определяет остальные. Обратите внимание, что u также зависит от m . Некоторые дополнительные отношения с участием вас включают $$\cos \varphi =\operatorname {cn} u,\quad {\textrm {and}}\quad {\sqrt {1-m\sin ^{2}\varphi }}=\operatorname {dn} u.$$

Последнюю иногда называют дельта-амплитудой и записывают как Δ( φ ) = dn u . Иногда в литературе также упоминаются дополнительный параметр , дополнительный модуль или дополнительный модульный угол . Более подробно они определены в статье о квартальных периодах .

В этом обозначении использование вертикальной черты в качестве разделителя указывает, что аргумент, следующий за ней, является «параметром» (как определено выше), а обратная косая черта указывает, что это модульный угол. Использование точки с запятой подразумевает, что предшествующий ей аргумент представляет собой синус амплитуды: $$F(\varphi ,\sin \alpha )=F\left(\varphi \mid \sin ^{2}\alpha \right)=F(\varphi \setminus \alpha )=F(\sin \varphi ;\sin \alpha ).$$Это потенциально сбивающее с толку использование различных разделителей аргументов является традиционным для эллиптических интегралов, и большая часть обозначений совместима с обозначениями, используемыми в справочнике Абрамовица и Стегуна, а также с обозначениями, используемыми в интегральных таблицах Градштейна и Рыжика .

В литературе используются и другие соглашения об обозначениях эллиптических интегралов. обозначение с переставленными аргументами F ( k , φ ) Часто встречается ; и аналогично E ( k , φ ) для интеграла второго рода. Абрамовиц и Стеган на интеграл первого рода F ( φ , k ) заменили аргумент φ в своем определении интегралов второго и третьего рода, если только за этим аргументом не стоит вертикальная черта: т. е. E ( F ( φ , к ) | ² ) для E ( φ | k ² ) . Более того, их полные интегралы используют параметр k ² в качестве аргумента вместо модуля k , т.е. K ( k ² ), а не K ( k ) . А интеграл третьего рода, определенный Градштейном и Рыжиком , Π( φ , n , k ) , ставит на первое место амплитуду φ , а не «характеристику» n .

Таким образом, при использовании этих функций следует быть осторожным с обозначениями, поскольку в различных авторитетных справочниках и пакетах программного обеспечения используются разные соглашения в определениях эллиптических функций. Например, Wolfram компании программное обеспечение Mathematica и Wolfram Alpha определяют полный эллиптический интеграл первого рода через параметр m вместо эллиптического модуля k .

Неполный эллиптический интеграл первого рода

Неполный эллиптический интеграл первого рода F определяется как

$$F(\varphi ,k)=F\left(\varphi \mid k^{2}\right)=F(\sin \varphi ;k)=\int _{0}^{\varphi }{\frac {d\theta }{\sqrt {1-k^{2}\sin ^{2}\theta }}}.$$

Это тригонометрическая форма интеграла; подставляя t = sin θ и x = sin φ , получаем нормальную форму Лежандра:

$$F(x;k)=\int _{0}^{x}{\frac {dt}{\sqrt {\left(1-t^{2}\right)\left(1-k^{2}t^{2}\right)}}}.$$

Эквивалентно, с точки зрения амплитуды и модульного угла: $$F(\varphi \setminus \alpha )=F(\varphi ,\sin \alpha )=\int _{0}^{\varphi }{\frac {d\theta }{\sqrt {1-\left(\sin \theta \sin \alpha \right)^{2}}}}.$$

При x = sn( u , k ) имеем: $$F(x;k)=u;$$демонстрируя, что эта эллиптическая функция Якоби является простой обратной функцией неполного эллиптического интеграла первого рода.

Неполный эллиптический интеграл первого рода имеет следующую теорему сложения : $$F{\bigl [}\arctan(x),k{\bigr ]}+F{\bigl [}\arctan(y),k{\bigr ]}=F\left[\arctan \left({\frac {x{\sqrt {k'^{2}y^{2}+1}}}{\sqrt {y^{2}+1}}}\right)+\arctan \left({\frac {y{\sqrt {k'^{2}x^{2}+1}}}{\sqrt {x^{2}+1}}}\right),k\right]$$

Эллиптический модуль можно преобразовать следующим образом: $$F{\bigl [}\arcsin(x),k{\bigr ]}={\frac {2}{1+{\sqrt {1-k^{2}}}}}F\left[\arcsin \left({\frac {\left(1+{\sqrt {1-k^{2}}}\right)x}{1+{\sqrt {1-k^{2}x^{2}}}}}\right),{\frac {1-{\sqrt {1-k^{2}}}}{1+{\sqrt {1-k^{2}}}}}\right]$$

Неполный эллиптический интеграл второго рода

Неполный эллиптический интеграл второго рода E в тригонометрической форме равен

$$E(\varphi ,k)=E\left(\varphi \,|\,k^{2}\right)=E(\sin \varphi ;k)=\int _{0}^{\varphi }{\sqrt {1-k^{2}\sin ^{2}\theta }}\,d\theta .$$

Подставляя t = sin θ и x = sin φ , получаем нормальную форму Лежандра:

$$E(x;k)=\int _{0}^{x}{\frac {\sqrt {1-k^{2}t^{2}}}{\sqrt {1-t^{2}}}}\,dt.$$

Эквивалентно, с точки зрения амплитуды и модулярного угла: $$E(\varphi \setminus \alpha )=E(\varphi ,\sin \alpha )=\int _{0}^{\varphi }{\sqrt {1-\left(\sin \theta \sin \alpha \right)^{2}}}\,d\theta .$$

Связи с эллиптическими функциями Якоби включают $${\begin{aligned}E{\left(\operatorname {sn} (u;k);k\right)}=\int _{0}^{u}\operatorname {dn} ^{2}(w;k)\,dw&=u-k^{2}\int _{0}^{u}\operatorname {sn} ^{2}(w;k)\,dw\\[1ex]&=\left(1-k^{2}\right)u+k^{2}\int _{0}^{u}\operatorname {cn} ^{2}(w;k)\,dw.\end{aligned}}$$

от Длина дуги меридиана экватора до широты φ выражается через E : $$m(\varphi )=a\left(E(\varphi ,e)+{\frac {d^{2}}{d\varphi ^{2}}}E(\varphi ,e)\right),$$где а — большая полуось , а е — эксцентриситет .

Неполный эллиптический интеграл второго рода имеет следующую теорему сложения : $$E{\left[\arctan(x),k\right]}+E{\left[\arctan(y),k\right]}=E{\left[\arctan \left({\frac {x{\sqrt {k'^{2}y^{2}+1}}}{\sqrt {y^{2}+1}}}\right)+\arctan \left({\frac {y{\sqrt {k'^{2}x^{2}+1}}}{\sqrt {x^{2}+1}}}\right),k\right]}+{\frac {k^{2}xy}{k'^{2}x^{2}y^{2}+x^{2}+y^{2}+1}}\left({\frac {x{\sqrt {k'^{2}y^{2}+1}}}{\sqrt {y^{2}+1}}}+{\frac {y{\sqrt {k'^{2}x^{2}+1}}}{\sqrt {x^{2}+1}}}\right)$$

Эллиптический модуль можно преобразовать следующим образом: $$E{\left[\arcsin(x),k\right]}=\left(1+{\sqrt {1-k^{2}}}\right)E{\left[\arcsin \left({\frac {\left(1+{\sqrt {1-k^{2}}}\right)x}{1+{\sqrt {1-k^{2}x^{2}}}}}\right),{\frac {1-{\sqrt {1-k^{2}}}}{1+{\sqrt {1-k^{2}}}}}\right]}-{\sqrt {1-k^{2}}}F{\left[\arcsin(x),k\right]}+{\frac {k^{2}x{\sqrt {1-x^{2}}}}{1+{\sqrt {1-k^{2}x^{2}}}}}$$

Неполный эллиптический интеграл третьего рода

Неполный эллиптический интеграл третьего рода Π равен $$\Pi (n;\varphi \setminus \alpha )=\int _{0}^{\varphi }{\frac {1}{1-n\sin ^{2}\theta }}{\frac {d\theta }{\sqrt {1-\left(\sin \theta \sin \alpha \right)^{2}}}}$$

или

$$\Pi (n;\varphi \,|\,m)=\int _{0}^{\sin \varphi }{\frac {1}{1-nt^{2}}}{\frac {dt}{\sqrt {\left(1-mt^{2}\right)\left(1-t^{2}\right)}}}.$$

Число n называется характеристикой и может принимать любое значение независимо от других аргументов. Однако обратите внимание, что значение Π(1; ⁠ π / 2 ⁠ | m ) бесконечно для любого m .

Связь с эллиптическими функциями Якобиана такова: $$\Pi {\bigl (}n;\,\operatorname {am} (u;k);\,k{\bigr )}=\int _{0}^{u}{\frac {dw}{1-n\,\operatorname {sn} ^{2}(w;k)}}.$$

Длина дуги меридиана от экватора до широты φ также связана с частным случаем Π :

$$m(\varphi )=a\left(1-e^{2}\right)\Pi \left(e^{2};\varphi \,|\,e^{2}\right).$$

Полный эллиптический интеграл первого рода

График полного эллиптического интеграла первого рода K ( k )

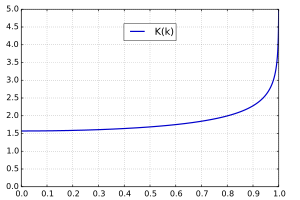
Эллиптические интегралы называются «полными», если амплитуда φ = ⁠ π / 2 ⁠ и, следовательно, x знак равно 1 . Таким образом, полный эллиптический интеграл первого рода K можно определить как $$K(k)=\int _{0}^{\tfrac {\pi }{2}}{\frac {d\theta }{\sqrt {1-k^{2}\sin ^{2}\theta }}}=\int _{0}^{1}{\frac {dt}{\sqrt {\left(1-t^{2}\right)\left(1-k^{2}t^{2}\right)}}},$$или более компактно через неполный интеграл первого рода как $$K(k)=F\left({\tfrac {\pi }{2}},k\right)=F\left({\tfrac {\pi }{2}}\,|\,k^{2}\right)=F(1;k).$$

Его можно выразить в виде степенного ряда $$K(k)={\frac {\pi }{2}}\sum _{n=0}^{\infty }\left({\frac {(2n)!}{2^{2n}(n!)^{2}}}\right)^{2}k^{2n}={\frac {\pi }{2}}\sum _{n=0}^{\infty }{\bigl (}P_{2n}(0){\bigr )}^{2}k^{2n},$$

где P _n — полиномы Лежандра , что эквивалентно

$$K(k)={\frac {\pi }{2}}\left(1+\left({\frac {1}{2}}\right)^{2}k^{2}+\left({\frac {1\cdot 3}{2\cdot 4}}\right)^{2}k^{4}+\cdots +\left({\frac {\left(2n-1\right)!!}{\left(2n\right)!!}}\right)^{2}k^{2n}+\cdots \right),$$

где н !! обозначает двойной факториал . В терминах гипергеометрической функции Гаусса полный эллиптический интеграл первого рода можно выразить как

$$K(k)={\tfrac {\pi }{2}}\,{}_{2}F_{1}\left({\tfrac {1}{2}},{\tfrac {1}{2}};1;k^{2}\right).$$

Полный эллиптический интеграл первого рода иногда называют четвертьпериодом . Его можно очень эффективно вычислить с точки зрения среднего арифметико-геометрического : $$K(k)={\frac {\pi }{2\operatorname {agm} \left(1,{\sqrt {1-k^{2}}}\right)}}.$$

Следовательно, модуль можно преобразовать как:

$${\begin{aligned}K(k)&={\frac {\pi }{2\operatorname {agm} \left(1,{\sqrt {1-k^{2}}}\right)}}\\[4pt]&={\frac {\pi }{2\operatorname {agm} \left({\frac {1}{2}}+{\frac {\sqrt {1-k^{2}}}{2}},{\sqrt[{4}]{1-k^{2}}}\right)}}\\[4pt]&={\frac {\pi }{\left(1+{\sqrt {1-k^{2}}}\right)\operatorname {agm} \left(1,{\frac {2{\sqrt[{4}]{1-k^{2}}}}{\left(1+{\sqrt {1-k^{2}}}\right)}}\right)}}\\[4pt]&={\frac {2}{1+{\sqrt {1-k^{2}}}}}K\left({\frac {1-{\sqrt {1-k^{2}}}}{1+{\sqrt {1-k^{2}}}}}\right)\end{aligned}}$$

Это выражение справедливо для всех $n\in \mathbb {N}$ и 0 ≤ k ≤ 1 :

$$K(k)=n\left[\sum _{a=1}^{n}\operatorname {dn} \left({\frac {2a}{n}}K(k);k\right)\right]^{-1}K\left[k^{n}\prod _{a=1}^{n}\operatorname {sn} \left({\frac {2a-1}{n}}K(k);k\right)^{2}\right]$$

Связь с гамма-функцией

Если к ² знак равно λ ( я √ р ) и $r\in \mathbb {Q} ^{+}$ (где λ — модулярная лямбда-функция ), то K ( k ) выражается в замкнутой форме через гамма-функцию . Например, r = 2 , r = 3 и r = 7 дают соответственно:

$$K\left({\sqrt {2}}-1\right)={\frac {\Gamma \left({\frac {1}{8}}\right)\Gamma \left({\frac {3}{8}}\right){\sqrt {{\sqrt {2}}+1}}}{8{\sqrt[{4}]{2}}{\sqrt {\pi }}}},$$

и

$$K\left({\frac {{\sqrt {3}}-1}{2{\sqrt {2}}}}\right)={\frac {1}{8\pi }}{\sqrt[{4}]{3}}\,{\sqrt[{3}]{4}}\,\Gamma {\biggl (}{\frac {1}{3}}{\biggr )}^{3}$$

и

$$K\left({\frac {3-{\sqrt {7}}}{4{\sqrt {2}}}}\right)={\frac {\Gamma \left({\frac {1}{7}}\right)\Gamma \left({\frac {2}{7}}\right)\Gamma \left({\frac {4}{7}}\right)}{4{\sqrt[{4}]{7}}\pi }}.$$

В более общем смысле, условие, $${\frac {iK'}{K}}={\frac {iK\left({\sqrt {1-k^{2}}}\right)}{K(k)}}$$находиться в воображаемом квадратичном поле достаточно. Например, если k = e ^{5 πи /6} , затем ⁠ iK ′ / K ⁠ знак равно е ^{2 πи /3} и

$$K\left(e^{5\pi i/6}\right)={\frac {e^{-\pi i/12}\Gamma ^{3}\left({\frac {1}{3}}\right){\sqrt[{4}]{3}}}{4{\sqrt[{3}]{2}}\pi }}.$$

Связь с тета-функцией Якоби

Связь с тэта-функцией Якоби определяется выражением $$K(k)={\frac {\pi }{2}}\theta _{3}^{2}(q),$$где имя q ​ $$q(k)=\exp \left(-\pi {\frac {K\left({\sqrt {1-k^{2}}}\right)}{K(k)}}\right).$$

Асимптотические выражения

$$K\left(k\right)\approx {\frac {\pi }{2}}+{\frac {\pi }{8}}{\frac {k^{2}}{1-k^{2}}}-{\frac {\pi }{16}}{\frac {k^{4}}{1-k^{2}}}$$Это приближение имеет относительную точность лучше, чем 3 × 10. ⁻⁴ для к < ⁠ 1/2 ​ ⁠ ​ . Сохранение только первых двух членов правильно с точностью до 0,01 для k < ⁠ 1 / 2 ⁠ .

Дифференциальное уравнение

Дифференциальное уравнение для эллиптического интеграла первого рода имеет вид $${\frac {d}{dk}}\left(k\left(1-k^{2}\right){\frac {dK(k)}{dk}}\right)=k\,K(k)$$

Второе решение этого уравнения: $K\left({\sqrt {1-k^{2}}}\right)$. Это решение удовлетворяет соотношению $${\frac {d}{dk}}K(k)={\frac {E(k)}{k\left(1-k^{2}\right)}}-{\frac {K(k)}{k}}.$$

Непрерывная дробь

Расширение непрерывной дроби : $${\frac {K(k)}{2\pi }}=-{\frac {1}{4}}+\sum _{n=0}^{\infty }{\frac {q^{n}}{1+q^{2n}}}=-{\frac {1}{4}}+{\cfrac {1}{1-q+{\cfrac {\left(1-q\right)^{2}}{1-q^{3}+{\cfrac {q\left(1-q^{2}\right)^{2}}{1-q^{5}+{\cfrac {q^{2}\left(1-q^{3}\right)^{2}}{1-q^{7}+{\cfrac {q^{3}\left(1-q^{4}\right)^{2}}{1-q^{9}+\cdots }}}}}}}}}},$$где ном этот $q=q(k)=\exp[-\pi K'(k)/K(k)]$ в его определении.

Полный эллиптический интеграл второго рода

График полного эллиптического интеграла второго рода E ( k )

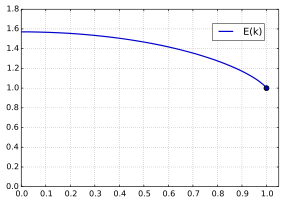
Полный эллиптический интеграл второго рода E определяется как

$$E(k)=\int _{0}^{\tfrac {\pi }{2}}{\sqrt {1-k^{2}\sin ^{2}\theta }}\,d\theta =\int _{0}^{1}{\frac {\sqrt {1-k^{2}t^{2}}}{\sqrt {1-t^{2}}}}\,dt,$$

или более компактно через неполный интеграл второго рода E ( φ , k ) как

$$E(k)=E\left({\tfrac {\pi }{2}},k\right)=E(1;k).$$

Для эллипса с большой полуосью a и малой полуосью b и эксцентриситетом e = √ 1 − b ² / а ² , полный эллиптический интеграл второго рода E ( e ) равен одной четверти длины окружности C эллипса, измеренной в единицах большой полуоси a . Другими словами:

$$C=4aE(e).$$

Полный эллиптический интеграл второго рода можно выразить в виде степенного ряда

$$E(k)={\frac {\pi }{2}}\sum _{n=0}^{\infty }\left({\frac {(2n)!}{2^{2n}\left(n!\right)^{2}}}\right)^{2}{\frac {k^{2n}}{1-2n}},$$

что эквивалентно

$$E(k)={\frac {\pi }{2}}\left(1-\left({\frac {1}{2}}\right)^{2}{\frac {k^{2}}{1}}-\left({\frac {1\cdot 3}{2\cdot 4}}\right)^{2}{\frac {k^{4}}{3}}-\cdots -\left({\frac {(2n-1)!!}{(2n)!!}}\right)^{2}{\frac {k^{2n}}{2n-1}}-\cdots \right).$$

В терминах гипергеометрической функции Гаусса полный эллиптический интеграл второго рода можно выразить как

$$E(k)={\tfrac {\pi }{2}}\,{}_{2}F_{1}\left({\tfrac {1}{2}},-{\tfrac {1}{2}};1;k^{2}\right).$$

Модуль можно преобразовать следующим образом: $$E(k)=\left(1+{\sqrt {1-k^{2}}}\right)\,E\left({\frac {1-{\sqrt {1-k^{2}}}}{1+{\sqrt {1-k^{2}}}}}\right)-{\sqrt {1-k^{2}}}\,K(k)$$

Вычисление

Как и интеграл первого рода, полный эллиптический интеграл второго рода можно очень эффективно вычислить, используя среднее арифметико-геометрическое .

Определим последовательности a _n и g _n , где a ₀ = 1 , g ₀ = √ 1 − k ² = k ′ и рекуррентные соотношения a _{n + 1} = ⁠ а _п + грамм _п / 2 ⁠ , грамм _{п + 1} знак равно √ а _п грамм _{п верно} . Кроме того, определите $$c_{n}={\sqrt {\left|a_{n}^{2}-g_{n}^{2}\right|}}.$$

По определению,

$$a_{\infty }=\lim _{n\to \infty }a_{n}=\lim _{n\to \infty }g_{n}=\operatorname {agm} \left(1,{\sqrt {1-k^{2}}}\right).$$

Также

$$\lim _{n\to \infty }c_{n}=0.$$

Затем

$$E(k)={\frac {\pi }{2a_{\infty }}}\left(1-\sum _{n=0}^{\infty }2^{n-1}c_{n}^{2}\right).$$

На практике среднее арифметико-геометрическое будет просто вычисляться до некоторого предела. Эта формула сходится квадратично для всех | к | ≤ 1 . Для дальнейшего ускорения вычислений соотношение c _{n + 1} = ⁠ c _n ² / 4 a _{n + 1} ⁠ можно использовать.

Кроме того, если к ² знак равно λ ( я √ р ) и $r\in \mathbb {Q} ^{+}$ (где λ — модулярная лямбда-функция ), то E ( k ) выражается в замкнутой форме через $$K(k)={\frac {\pi }{2\operatorname {agm} \left(1,{\sqrt {1-k^{2}}}\right)}}$$и, следовательно, может быть вычислено без необходимости использования бесконечного члена суммирования. Например, r = 1 , r = 3 и r = 7 дают соответственно:

$$E\left({\frac {1}{\sqrt {2}}}\right)={\frac {1}{2}}K\left({\frac {1}{\sqrt {2}}}\right)+{\frac {\pi }{4K\left({\frac {1}{\sqrt {2}}}\right)}},$$

и

$$E\left({\frac {{\sqrt {3}}-1}{2{\sqrt {2}}}}\right)={\frac {3+{\sqrt {3}}}{6}}K\left({\frac {{\sqrt {3}}-1}{2{\sqrt {2}}}}\right)+{\frac {\pi {\sqrt {3}}}{12K\left({\frac {{\sqrt {3}}-1}{2{\sqrt {2}}}}\right)}},$$

и

$$E\left({\frac {3-{\sqrt {7}}}{4{\sqrt {2}}}}\right)={\frac {7+2{\sqrt {7}}}{14}}K\left({\frac {3-{\sqrt {7}}}{4{\sqrt {2}}}}\right)+{\frac {\pi {\sqrt {7}}}{28K\left({\frac {3-{\sqrt {7}}}{4{\sqrt {2}}}}\right)}}.$$

Производное и дифференциальное уравнение

$${\frac {dE(k)}{dk}}={\frac {E(k)-K(k)}{k}}$$$$\left(k^{2}-1\right){\frac {d}{dk}}\left(k\;{\frac {dE(k)}{dk}}\right)=kE(k)$$

Вторым решением этого уравнения является E ( √ 1 − k ² ) - K ( √ 1 - k ² ) .

Полный эллиптический интеграл третьего рода

График полного эллиптического интеграла третьего рода Π( n , k ) с несколькими фиксированными значениями n

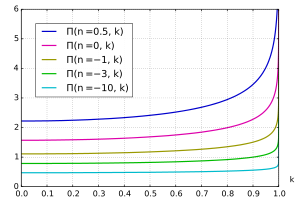
Полный эллиптический интеграл третьего рода Π можно определить как

$$\Pi (n,k)=\int _{0}^{\frac {\pi }{2}}{\frac {d\theta }{\left(1-n\sin ^{2}\theta \right){\sqrt {1-k^{2}\sin ^{2}\theta }}}}.$$

Заметим, что иногда эллиптический интеграл третьего рода определяется с обратным знаком характеристики n : $$\Pi '(n,k)=\int _{0}^{\frac {\pi }{2}}{\frac {d\theta }{\left(1+n\sin ^{2}\theta \right){\sqrt {1-k^{2}\sin ^{2}\theta }}}}.$$

Как и полные эллиптические интегралы первого и второго рода, полный эллиптический интеграл третьего рода можно очень эффективно вычислить, используя среднее арифметико-геометрическое.

Частные производные

$${\begin{aligned}{\frac {\partial \Pi (n,k)}{\partial n}}&={\frac {1}{2\left(k^{2}-n\right)(n-1)}}\left(E(k)+{\frac {1}{n}}\left(k^{2}-n\right)K(k)+{\frac {1}{n}}\left(n^{2}-k^{2}\right)\Pi (n,k)\right)\\[8pt]{\frac {\partial \Pi (n,k)}{\partial k}}&={\frac {k}{n-k^{2}}}\left({\frac {E(k)}{k^{2}-1}}+\Pi (n,k)\right)\end{aligned}}$$

Дзета-функция Якоби

В 1829 году Якоби определил дзета-функцию Якоби : $$Z(\varphi ,k)=E(\varphi ,k)-{\frac {E(k)}{K(k)}}F(\varphi ,k).$$Оно носит периодический характер $\varphi$ с минимальным периодом $\pi$. Она связана с функцией Якоби zn соотношением $Z(\varphi ,k)=\operatorname {zn} (F(\varphi ,k),k)$. В литературе (например, Whittaker and Watson (1927)), иногда $Z$ означает Википедию $\operatorname {zn}$. Некоторые авторы (например, Кинг (1924)) используют $Z$ для обеих Википедии $Z$ и $\operatorname {zn}$.

Отношение Лежандра

или Отношение Лежандра тождество Лежандра показывает отношение интегралов K и E эллиптического модуля и его анти-связанного аналога. в интегральном уравнении второй степени:

Для двух модулей, которые являются пифагорейскими аналогами друг друга, это соотношение справедливо:

$$K(\varepsilon )E\left({\sqrt {1-\varepsilon ^{2}}}\right)+E(\varepsilon )K\left({\sqrt {1-\varepsilon ^{2}}}\right)-K(\varepsilon )K\left({\sqrt {1-\varepsilon ^{2}}}\right)={\frac {\pi }{2}}$$

Например:

$K({\color {blueviolet}{\tfrac {3}{5}}})E({\color {blue}{\tfrac {4}{5}}})+E({\color {blueviolet}{\tfrac {3}{5}}})K({\color {blue}{\tfrac {4}{5}}})-K({\color {blueviolet}{\tfrac {3}{5}}})K({\color {blue}{\tfrac {4}{5}}})={\tfrac {1}{2}}\pi$

А для двух модулей, являющихся тангенциальными аналогами друг друга, справедливо следующее соотношение:

$(1+\varepsilon )K(\varepsilon )E({\tfrac {1-\varepsilon }{1+\varepsilon }})+{\tfrac {2}{1+\varepsilon }}E(\varepsilon )K({\tfrac {1-\varepsilon }{1+\varepsilon }})-2K(\varepsilon )K({\tfrac {1-\varepsilon }{1+\varepsilon }})={\tfrac {1}{2}}\pi$

Например:

${\tfrac {4}{3}}K({\color {blue}{\tfrac {1}{3}}})E({\color {green}{\tfrac {1}{2}}})+{\tfrac {3}{2}}E({\color {blue}{\tfrac {1}{3}}})K({\color {green}{\tfrac {1}{2}}})-2K({\color {blue}{\tfrac {1}{3}}})K({\color {green}{\tfrac {1}{2}}})={\tfrac {1}{2}}\pi$

Соотношение Лежандра для тангенциальных модульных аналогов вытекает непосредственно из тождества Лежандра для пифагорейских модульных аналогов с использованием модульного преобразования Ландена для пифагорейского противомодуля.

Особое тождество для лемнискатического случая

Для лемнискатического случая эллиптический модуль или удельный эксцентриситет ε равен половине квадратного корня из двух. Тождество Лежандра для лемнискатического случая можно доказать следующим образом:

Согласно правилу Цепи, эти деривативы имеют следующее соотношение:

${\frac {\mathrm {d} }{\mathrm {d} y}}\,K{\bigl (}{\frac {1}{2}}{\sqrt {2}}{\bigr )}-F{\biggl [}\arccos(xy);{\frac {1}{2}}{\sqrt {2}}{\biggr ]}={\frac {{\sqrt {2}}\,x}{\sqrt {1-x^{4}y^{4}}}}$

${\frac {\mathrm {d} }{\mathrm {d} y}}\,2E{\bigl (}{\frac {1}{2}}{\sqrt {2}}{\bigr )}-K{\bigl (}{\frac {1}{2}}{\sqrt {2}}{\bigr )}-2E{\biggl [}\arccos(xy);{\frac {1}{2}}{\sqrt {2}}{\biggr ]}+F{\biggl [}\arccos(xy);{\frac {1}{2}}{\sqrt {2}}{\biggr ]}={\frac {{\sqrt {2}}\,x^{3}y^{2}}{\sqrt {1-x^{4}y^{4}}}}$

Используя Фундаментальную теорему исчисления, можно получить следующие формулы:

$K{\bigl (}{\frac {1}{2}}{\sqrt {2}}{\bigr )}-F{\biggl [}\arccos(x);{\frac {1}{2}}{\sqrt {2}}{\biggr ]}=\int _{0}^{1}{\frac {{\sqrt {2}}\,x}{\sqrt {1-x^{4}y^{4}}}}\,\mathrm {d} y$

$2E{\bigl (}{\frac {1}{2}}{\sqrt {2}}{\bigr )}-K{\bigl (}{\frac {1}{2}}{\sqrt {2}}{\bigr )}-2E{\biggl [}\arccos(x);{\frac {1}{2}}{\sqrt {2}}{\biggr ]}+F{\biggl [}\arccos(x);{\frac {1}{2}}{\sqrt {2}}{\biggr ]}=\int _{0}^{1}{\frac {{\sqrt {2}}\,x^{3}y^{2}}{\sqrt {1-x^{4}y^{4}}}}\,\mathrm {d} y$

Линейная комбинация двух уже упомянутых интегралов приводит к следующей формуле:

${\frac {\sqrt {2}}{\sqrt {1-x^{4}}}}{\biggl \{}2E{\bigl (}{\frac {1}{2}}{\sqrt {2}}{\bigr )}-K{\bigl (}{\frac {1}{2}}{\sqrt {2}}{\bigr )}-2E{\biggl [}\arccos(x);{\frac {1}{2}}{\sqrt {2}}{\biggr ]}+F{\biggl [}\arccos(x);{\frac {1}{2}}{\sqrt {2}}{\biggr ]}{\biggr \}}\,+$

$+\,{\frac {{\sqrt {2}}\,x^{2}}{\sqrt {1-x^{4}}}}{\biggl \{}K{\bigl (}{\frac {1}{2}}{\sqrt {2}}{\bigr )}-F{\biggl [}\arccos(x);{\frac {1}{2}}{\sqrt {2}}{\biggr ]}{\biggr \}}=\int _{0}^{1}{\frac {2\,x^{3}(y^{2}+1)}{\sqrt {(1-x^{4})(1-x^{4}\,y^{4})}}}\,\mathrm {d} y$

Формируя исходную первообразную, связанную с x, из функции, показанной теперь с использованием правила произведения, получается следующая формула:

${\biggl \{}K{\bigl (}{\frac {1}{2}}{\sqrt {2}}{\bigr )}-F{\biggl [}\arccos(x);{\frac {1}{2}}{\sqrt {2}}{\biggr ]}{\biggr \}}{\biggl \{}2E{\bigl (}{\frac {1}{2}}{\sqrt {2}}{\bigr )}-K{\bigl (}{\frac {1}{2}}{\sqrt {2}}{\bigr )}-2E{\biggl [}\arccos(x);{\frac {1}{2}}{\sqrt {2}}{\biggr ]}+F{\biggl [}\arccos(x);{\frac {1}{2}}{\sqrt {2}}{\biggr ]}{\biggr \}}=$

$=\int _{0}^{1}{\frac {1}{y^{2}}}(y^{2}+1){\biggl [}{\text{artanh}}(y^{2})-{\text{artanh}}{\bigl (}{\frac {{\sqrt {1-x^{4}}}\,y^{2}}{\sqrt {1-x^{4}y^{4}}}}{\bigr )}{\biggr ]}\mathrm {d} y$

Если значение $x=1$ вставляется в это целостное тождество, то возникает тождество:

$K{\bigl (}{\frac {1}{2}}{\sqrt {2}}{\bigr )}{\biggl [}2\,E{\bigl (}{\frac {1}{2}}{\sqrt {2}}{\bigr )}-K{\bigl (}{\frac {1}{2}}{\sqrt {2}}{\bigr )}{\biggr ]}=\int _{0}^{1}{\frac {1}{y^{2}}}(y^{2}+1)\,{\text{artanh}}(y^{2})\,\mathrm {d} y=$

$={\biggl [}2\arctan(y)-{\frac {1}{y}}(1-y^{2})\,{\text{artanh}}(y^{2}){\biggr ]}_{y=0}^{y=1}=2\arctan(1)={\frac {\pi }{2}}$

Вот как выглядит этот лемнискатический отрывок из личности Лежандра:

$2E{\bigl (}{\frac {1}{2}}{\sqrt {2}}{\bigr )}K{\bigl (}{\frac {1}{2}}{\sqrt {2}}{\bigr )}-K{\bigl (}{\frac {1}{2}}{\sqrt {2}}{\bigr )}^{2}={\frac {\pi }{2}}$

Обобщение на общий случай

Теперь модульный общий случай отработано. Для этого производные полных эллиптических интегралов выводятся по модулю $\varepsilon$ а затем они объединяются. И тогда баланс личности Лежандра определяется.

Потому что производная функции круга является отрицательным произведением идентичной функции отображения и обратной функции круга:

${\frac {\mathrm {d} }{\mathrm {d} \varepsilon }}{\sqrt {1-\varepsilon ^{2}}}=-\,{\frac {\varepsilon }{\sqrt {1-\varepsilon ^{2}}}}$

Это производные K и E, показанные в этой статье в разделах выше:

${\frac {\mathrm {d} }{\mathrm {d} \varepsilon }}K(\varepsilon )={\frac {1}{\varepsilon (1-\varepsilon ^{2})}}{\bigl [}E(\varepsilon )-(1-\varepsilon ^{2})K(\varepsilon ){\bigr ]}$

${\frac {\mathrm {d} }{\mathrm {d} \varepsilon }}E(\varepsilon )=-\,{\frac {1}{\varepsilon }}{\bigl [}K(\varepsilon )-E(\varepsilon ){\bigr ]}$

В сочетании с производной функции окружности эти производные действительны тогда:

${\frac {\mathrm {d} }{\mathrm {d} \varepsilon }}K({\sqrt {1-\varepsilon ^{2}}})={\frac {1}{\varepsilon (1-\varepsilon ^{2})}}{\bigl [}\varepsilon ^{2}K({\sqrt {1-\varepsilon ^{2}}})-E({\sqrt {1-\varepsilon ^{2}}}){\bigr ]}$

${\frac {\mathrm {d} }{\mathrm {d} \varepsilon }}E({\sqrt {1-\varepsilon ^{2}}})={\frac {\varepsilon }{1-\varepsilon ^{2}}}{\bigl [}K({\sqrt {1-\varepsilon ^{2}}})-E({\sqrt {1-\varepsilon ^{2}}}){\bigr ]}$

Тождество Лежандра включает произведения любых двух полных эллиптических интегралов. Для вывода стороны функции из шкалы уравнения тождества Лежандра правило произведения теперь применяется в следующем:

${\frac {\mathrm {d} }{\mathrm {d} \varepsilon }}K(\varepsilon )E({\sqrt {1-\varepsilon ^{2}}})={\frac {1}{\varepsilon (1-\varepsilon ^{2})}}{\bigl [}E(\varepsilon )E({\sqrt {1-\varepsilon ^{2}}})-K(\varepsilon )E({\sqrt {1-\varepsilon ^{2}}})+\varepsilon ^{2}K(\varepsilon )K({\sqrt {1-\varepsilon ^{2}}}){\bigr ]}$

${\frac {\mathrm {d} }{\mathrm {d} \varepsilon }}E(\varepsilon )K({\sqrt {1-\varepsilon ^{2}}})={\frac {1}{\varepsilon (1-\varepsilon ^{2})}}{\bigl [}-E(\varepsilon )E({\sqrt {1-\varepsilon ^{2}}})+E(\varepsilon )K({\sqrt {1-\varepsilon ^{2}}})-(1-\varepsilon ^{2})K(\varepsilon )K({\sqrt {1-\varepsilon ^{2}}}){\bigr ]}$

${\frac {\mathrm {d} }{\mathrm {d} \varepsilon }}K(\varepsilon )K({\sqrt {1-\varepsilon ^{2}}})={\frac {1}{\varepsilon (1-\varepsilon ^{2})}}{\bigl [}E(\varepsilon )K({\sqrt {1-\varepsilon ^{2}}})-K(\varepsilon )E({\sqrt {1-\varepsilon ^{2}}})-(1-2\varepsilon ^{2})K(\varepsilon )K({\sqrt {1-\varepsilon ^{2}}}){\bigr ]}$

Из этих трех уравнений сложение двух верхних уравнений и вычитание нижнего уравнения дает следующий результат:

${\frac {\mathrm {d} }{\mathrm {d} \varepsilon }}{\bigl [}K(\varepsilon )E({\sqrt {1-\varepsilon ^{2}}})+E(\varepsilon )K({\sqrt {1-\varepsilon ^{2}}})-K(\varepsilon )K({\sqrt {1-\varepsilon ^{2}}}){\bigr ]}=0$

По отношению к $\varepsilon$ уравнение баланса постоянно дает нулевое значение.

Полученный ранее результат необходимо объединить с уравнением Лежандра для модуля $\varepsilon =1/{\sqrt {2}}$ это описано в предыдущем разделе:

$2E{\bigl (}{\frac {1}{2}}{\sqrt {2}}{\bigr )}K{\bigl (}{\frac {1}{2}}{\sqrt {2}}{\bigr )}-K{\bigl (}{\frac {1}{2}}{\sqrt {2}}{\bigr )}^{2}={\frac {\pi }{2}}$

Комбинация последних двух формул дает следующий результат:

$K(\varepsilon )E({\sqrt {1-\varepsilon ^{2}}})+E(\varepsilon )K({\sqrt {1-\varepsilon ^{2}}})-K(\varepsilon )K({\sqrt {1-\varepsilon ^{2}}})={\tfrac {1}{2}}\pi$

Потому что, если производная непрерывной функции постоянно принимает нулевое значение, то рассматриваемая функция является постоянной функцией. Это означает, что эта функция дает одно и то же значение функции для каждого значения абсцисс. $\varepsilon$ и соответствующий график функции, следовательно, представляет собой горизонтальную прямую линию.

См. также

• Эллиптическая кривая
• Отображение Шварца – Кристоффеля
• Симметричная форма Карлсона
• Эллиптические функции Якоби
• Эллиптические функции Вейерштрасса
• Тета-функция Якоби
• Тета-функция Рамануджана
• Среднее арифметико-геометрическое
• Период маятника
• Меридианная дуга

Ссылки

Источники

• Абрамовиц, Милтон ; Стегун, Ирен Энн , ред. (1983) [июнь 1964 г.]. «Глава 17» . Справочник по математическим функциям с формулами, графиками и математическими таблицами . Серия «Прикладная математика». Том. 55 (Девятое переиздание с дополнительными исправлениями десятого оригинального издания с исправлениями (декабрь 1972 г.); первое изд.). Вашингтон, округ Колумбия; Нью-Йорк: Министерство торговли США, Национальное бюро стандартов; Дуврские публикации. п. 587. ИСБН  978-0-486-61272-0 . LCCN   64-60036 . МР   0167642 . LCCN   65-12253 .
• Берд, ПФ; Фридман, доктор медицины (1971). Справочник по эллиптическим интегралам для инженеров и ученых (2-е изд.). Нью-Йорк: Springer-Verlag. ISBN  0-387-05318-2 .
• Карлсон, Британская Колумбия (1995). «Численное вычисление действительных или комплексных эллиптических интегралов». Численные алгоритмы . 10 (1): 13–26. arXiv : math/9409227 . Бибкод : 1995NuAlg..10...13C . дои : 10.1007/BF02198293 . S2CID   11580137 .
• Карлсон, Британская Колумбия (2010), «Эллиптический интеграл» , Олвер, Фрэнк У.Дж .; Лозье, Дэниел М.; Буасверт, Рональд Ф.; Кларк, Чарльз В. (ред.), Справочник NIST по математическим функциям , издательство Кембриджского университета, ISBN  978-0-521-19225-5 , МР   2723248 .
• Эрдели, Артур; Магнус, Вильгельм ; Оберхеттингер, Фриц; Трикоми, Франческо Г. (1953). Высшие трансцендентные функции. Том II (PDF) . McGraw-Hill Book Company, Inc., Нью-Йорк-Торонто-Лондон. МР   0058756 . Архивировано из оригинала (PDF) 14 июля 2011 г. Проверено 24 июля 2016 г.
• Градштейн Израиль Соломонович ; Рыжик Иосиф Моисеевич ; Героним Юрий Вениаминович ; Цейтлин Михаил Юльевич ; Джеффри, Алан (2015) [октябрь 2014 г.]. «8.1.». В Цвиллингере, Дэниел; Молл, Виктор Гюго (ред.). Таблица интегралов, рядов и произведений . Перевод Scripta Technica, Inc. (8-е изд.). Academic Press, Inc. ISBN  978-0-12-384933-5 . LCCN   2014010276 .
• Гринхилл, Альфред Джордж (1892). Приложения эллиптических функций . Нью-Йорк: Макмиллан.
• Хэнкок, Харрис (1910). Лекции по теории эллиптических функций . Нью-Йорк: Дж. Уайли и сыновья.
• Король, Луи В. (1924). О прямом численном вычислении эллиптических функций и интегралов . Издательство Кембриджского университета.
• Пресс, WH; Теукольский, С.А.; Феттерлинг, WT; Фланнери, Б.П. (2007), «Раздел 6.12. Эллиптические интегралы и эллиптические функции Якоби» , Численные рецепты: искусство научных вычислений (3-е изд.), Нью-Йорк: Cambridge University Press, ISBN  978-0-521-88068-8 , заархивировано из оригинала 11 августа 2011 г. , получено 9 августа 2011 г.

Внешние ссылки

• «Эллиптический интеграл» , Математическая энциклопедия , EMS Press , 2001 [1994]
• Эрик В. Вайсштейн, «Эллиптический интеграл» (Mathworld)
• Код Matlab для оценки эллиптических интегралов с помощью эллиптического проекта
• Рациональные аппроксимации полных эллиптических интегралов (Exstrom Laboratories)
• Краткая история эллиптических теорем сложения интегралов