Пифагорейские средства

Геометрическая конструкция среднего квадратичного и среднего Пифагора (двух чисел a и b ). Среднее гармоническое, обозначаемое   H , геометрический по   G , арифметика по   A и среднее квадратичное (также известное как среднеквадратичное ), обозначаемое   Вопрос .

Сравнение средних арифметических, геометрических и гармонических пар чисел. Вертикальные пунктирные линии — асимптоты гармонических средних.

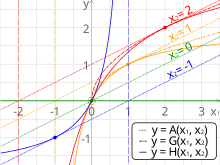
В математике три классических средних Пифагора — это среднее арифметическое (AM), среднее геометрическое (GM) и среднее гармоническое (HM). Эти средства изучались с помощью пропорций пифагорейцами и последующими поколениями греческих математиков. из-за их важности в геометрии и музыке.

Определение

Они определяются:

$${\begin{aligned}\operatorname {AM} \left(x_{1},\;\ldots ,\;x_{n}\right)&={\frac {x_{1}+\;\cdots \;+x_{n}}{n}}\\[9pt]\operatorname {GM} \left(x_{1},\;\ldots ,\;x_{n}\right)&={\sqrt[{n}]{\left\vert x_{1}\times \,\cdots \,\times x_{n}\right\vert }}\\[9pt]\operatorname {HM} \left(x_{1},\;\ldots ,\;x_{n}\right)&={\frac {n}{\displaystyle {\frac {1}{x_{1}}}+\;\cdots \;+{\frac {1}{x_{n}}}}}\end{aligned}}$$

Характеристики

Каждое означает, ${\textstyle \operatorname {M} }$, имеет следующие свойства:

первого порядка Однородность

$\operatorname {M} (bx_{1},\,\ldots ,\,bx_{n})=b\operatorname {M} (x_{1},\,\ldots ,\,x_{n})$

Инвариантность при обмене

$\operatorname {M} (\ldots ,\,x_{i},\,\ldots ,\,x_{j},\,\ldots )=\operatorname {M} (\ldots ,\,x_{j},\,\ldots ,\,x_{i},\,\ldots )$

для любого $i$ и $j$.

Монотонность

$a\leq b\rightarrow \operatorname {M} (a,x_{1},x_{2},\ldots x_{n})\leq \operatorname {M} (b,x_{1},x_{2},\ldots x_{n})$

Идемпотентность

$\forall x,\;M(x,x,\ldots x)=x$

Монотонность и идемпотентность вместе означают, что среднее значение набора всегда лежит между крайностями набора: $$\min(x_{1},\,\ldots ,\,x_{n})\leq \operatorname {M} (x_{1},\,\ldots ,\,x_{n})\leq \max(x_{1},\,\ldots ,\,x_{n}).$$

Гармонические и средние арифметические являются взаимно двойственными друг другу для положительных аргументов. $$\operatorname {HM} \left({\frac {1}{x_{1}}},\,\ldots ,\,{\frac {1}{x_{n}}}\right)={\frac {1}{\operatorname {AM} \left(x_{1},\,\ldots ,\,x_{n}\right)}},$$

в то время как среднее геометрическое является своим собственным обратным двойником: $$\operatorname {GM} \left({\frac {1}{x_{1}}},\,\ldots ,\,{\frac {1}{x_{n}}}\right)={\frac {1}{\operatorname {GM} \left(x_{1},\,\ldots ,\,x_{n}\right)}}.$$

Неравенство между средствами

Геометрическое доказательство без слов , что max ( a , b ) > среднеквадратичное ( RMS ) или среднее квадратичное ( QM ) > среднее арифметическое ( AM ) > среднее геометрическое ( GM ) > гармоническое ( HM ) > min ( a , b ) среднее два различных положительных числа a и b

Существует упорядоченность этих средств (если все $x_{i}$ положительные) $$\min \leq \operatorname {HM} \leq \operatorname {GM} \leq \operatorname {AM} \leq \max$$с равенством тогда и только тогда, когда $x_{i}$ все равны.

Это обобщение неравенства средних арифметических и геометрических и частный случай неравенства для обобщенных средних . Доказательство следует из среднего арифметико-геометрического неравенства : $\operatorname {AM} \leq \max$и обратная двойственность ( $\min$ и $\max$ также взаимно двойственны друг другу).

Изучение пифагорейских средних тесно связано с изучением мажоризации и выпуклых функций Шура . Гармонические и средние геометрические являются вогнутыми симметричными функциями своих аргументов и, следовательно, вогнутыми по Шуру, тогда как среднее арифметическое является линейной функцией своих аргументов и, следовательно, является одновременно вогнутым и выпуклым.

История

Почти все, что мы знаем о пифагорейских средних, взято из справочников по арифметике, написанных в первом и втором веке. Никомах Герасский говорит, что их «признавали все древние: Пифагор, Платон и Аристотель». Их самое раннее известное использование — это фрагмент из сочинения пифагорейского философа Архита Тарентского :

В музыке есть три средства: одно — арифметическое, второе — геометрическое, третье — субпротивное, которое называют гармоническим. Среднее является арифметическим, когда три члена пропорциональны так, что превышение, на которое первое превышает второе, равно тому, на которое второе превышает третье. В этой пропорции оказывается, что интервал больших членов меньше, а интервал меньших членов больше. Среднее значение является геометрическим, когда оно таково, что первое относится ко второму, а второе относится к третьему. Из этих членов интервал между большим и меньшим равен. Субпротивоположными, которые мы называем гармоническими, являются средние, когда они таковы, что в какой бы части себя первый член ни превышал второй, в той части третьего средний член превосходит третий. Оказывается, в этой пропорции интервал между большими членами больше, а между меньшими членами меньше.

Название «гармоническое среднее», по мнению Ямвлиха , было придумано Архитом и Гиппасом . Пифагорейские средства также появляются в Платона » «Тимее . Еще одним свидетельством их раннего использования является комментарий Паппа .

Именно [...] Теэтет отличил силы, соизмеримые по длине, от несоизмеримых, и разделил наиболее известные иррациональные линии различными способами, присвоив средние линии геометрии, биномиальные арифметике, и апотом гармонии, как утверждает Евдем , Перипатетик.

Термин «среднее» (μεσότης, mesótēs на древнегреческом языке) появляется в неопифагорейских справочниках по арифметике в связи с термином «пропорция» (ἀναλογία, на древнегреческом аналоге).

Наименьшее отдельное положительное целое число означает

а	б	ХМ	ГМ	ЯВЛЯЮСЬ
5	45	9	15	25
10	40	16	20	25

Из всех пар различных натуральных чисел формы ( a , b ) таких, что a < b , наименьшее (как определено наименьшим значением a + b ), для которого средние арифметические, геометрические и гармонические средние также являются натуральными числами, это ( 5, 45) и (10, 40).

См. также

• Среднее арифметико-геометрическое
• Средний
• Золотое сечение
• Треугольник Кеплера

Внешние ссылки

• Кантрелл, Дэвид В. «Пифагорейские средства» . Математический мир .