Граф продукта

В теории графов произведение графов — это бинарная операция над графами . В частности, это операция, которая берет два графа $G 1$ и $G 2$ и создает граф $H$ со следующими свойствами:

Множество вершин H $($ — это декартово произведение $V (G 1) \times V (G 2)$ , где $V и G 1)$ и $V (G 2)$ — множества вершин $G 1$ . $G 2$ соответственно
Две вершины $(a 1, a 2)$ и $(b 1, b 2)$ графа $H$ соединены ребром , если и только если условие относительно $a 1, b 1$ в $G 1$ и $a 2, b 2$ в $G 2$ выполнено.

Произведения графа различаются тем, в чем именно заключается это условие. равны или нет вершины $an,, bn Всегда речь идет о том$ в $G n$ или соединены ребром.

Терминология и обозначения для конкретных графовых продуктов в литературе довольно сильно различаются; даже если следующее можно считать несколько стандартным, читателям рекомендуется проверить, какое определение конкретный автор использует для графического продукта, особенно в старых текстах.

Даже для более стандартных определений в литературе не всегда единообразно, как обращаться с циклами . Приведенные ниже формулы для количества ребер в продукте также могут не работать при включении петель. Например, тензорное произведение одиночной вершинной петли на себя представляет собой другую одиночную вершинную петлю с $E=1$ , и не $E=2$ как формула $E_{G\times H}=2E_{G}E_{H}$ предложил бы.

Обзорная таблица

В следующей таблице показаны наиболее распространенные графические продукты с $\sim$ обозначающее «соединено ребром с», и $\not \sim$ обозначающий несмежность. Пока $\not \sim$ допускает равенство, $\not \simeq$ означает, что они должны быть различными и несмежными. Перечисленные здесь символы операторов ни в коем случае не являются стандартными, особенно в старых статьях.

Имя	Условие для $(a_{1},a_{2})\sim (b_{1},b_{2})$		Количество ребер ${\begin{array}{cc}v_{1}=\vert \mathrm {V} (G_{1})\vert &v_{2}=\vert \mathrm {V} (G_{2})\vert \\e_{1}=\vert \mathrm {E} (G_{1})\vert &e_{2}=\vert \mathrm {E} (G_{2})\vert \end{array}}$	Пример
Имя		с $a_{n}~{\text{rel}}~b_{n}$ сокращенно ${\text{rel}}_{n}$		Пример
Декартово произведение (коробочный продукт) 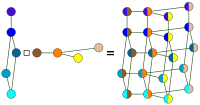$G_{1}\square G_{2}$	$a_{1}=b_{1}~\land ~a_{2}\sim b_{2}$ $\lor$ $a_{1}\sim b_{1}~\land ~a_{2}=b_{2}$	$=_{1}~\sim _{2}$ $\lor$ $\sim _{1}~=_{2}$	$v_{1}~e_{2}~+~e_{1}~v_{2}$
Тензорное произведение (произведение Кронекера, категориальный товар) $G_{1}\times G_{2}$	$a_{1}\sim b_{1}~\land ~a_{2}\sim b_{2}$	$\sim _{1}~\sim _{2}$	$2~e_{1}~e_{2}$
Лексикографический продукт $G_{1}\cdot G_{2}$ или $G_{1}[G_{2}]$	$a_{1}\sim b_{1}$ $\lor$ $a_{1}=b_{1}~\land ~a_{2}\sim b_{2}$	$\sim _{1}$ $\lor$ $=_{1}~\sim _{2}$	$v_{1}~e_{2}~+~e_{1}~v_{2}^{2}$
Сильный продукт (Нормальный продукт, И продукт) $G_{1}\boxtimes G_{2}$	$a_{1}=b_{1}~\land ~a_{2}\sim b_{2}$ $\lor$ $a_{1}\sim b_{1}~\land ~a_{2}=b_{2}$ $\lor$ $a_{1}\sim b_{1}~\land ~a_{2}\sim b_{2}$	$=_{1}~\sim _{2}$ $\lor$ $\sim _{1}~=_{2}$ $\lor$ $\sim _{1}~\sim _{2}$	$v_{1}~e_{2}~+~e_{1}~v_{2}~+~2~e_{1}~e_{2}$
Со-нормальный продукт (дизъюнктивное произведение, произведение ИЛИ) $G_{1}*G_{2}$	$a_{1}\sim b_{1}$ $\lor$ $a_{2}\sim b_{2}$	$\sim _{1}$ $\lor$ $\sim _{2}$	$v_{1}^{2}~e_{2}~+~e_{1}~v_{2}^{2}~-~2~e_{1}~e_{2}$
Модульный продукт	$a_{1}\sim b_{1}~\land ~a_{2}\sim b_{2}$ $\lor$ $a_{1}\not \simeq b_{1}~\land ~a_{2}\not \simeq b_{2}$	$\sim _{1}~\sim _{2}$ $\lor$ $\not \simeq _{1}~\not \simeq _{2}$
Укорененный продукт	см. статью		$v_{1}~e_{2}~+~e_{1}$
Зигзагообразное изделие	см. статью		см. статью	см. статью
Запасной продукт
Гомоморфный продукт ^[1]^[3] $G_{1}\ltimes G_{2}$	$a_{1}=b_{1}$ $\lor$ $a_{1}\sim b_{1}~\land ~a_{2}\not \sim b_{2}$	$=_{1}$ $\lor$ $\sim _{1}~\not \sim _{2}$	$v_{1}v_{2}(v_{2}-1)/2+e_{1}(v_{2}^{2}-2e_{2})$

В общем случае произведение графа определяется любым условием для $(a_{1},a_{2})\sim (b_{1},b_{2})$ что можно выразить через $a_{n}=b_{n}$ и $a_{n}\sim b_{n}$ .

Мнемоника

Позволять $K_{2}$ быть полным графом с двумя вершинами (т.е. с одним ребром). Графики продуктов $K_{2}\square K_{2}$ , $K_{2}\times K_{2}$ , и $K_{2}\boxtimes K_{2}$ выглядеть точно так же, как график, представляющий оператор. Например, $K_{2}\square K_{2}$ представляет собой четырехцикл (квадрат) и $K_{2}\boxtimes K_{2}$ — полный граф на четырех вершинах.

The $G_{1}[G_{2}]$ обозначение лексикографического произведения служит напоминанием о том, что это произведение не коммутативно. Полученный график выглядит как замена копии $G_{2}$ для каждой вершины $G_{1}$ .

См. также

Операции с графами

Примечания

^ Jump up to: ^а ^б Роберсон, Дэвид Э.; Манчинска, Лаура (2012). «Гомоморфизмы графов для квантовых игроков». Журнал комбинаторной теории, серия B. 118 : 228–267. arXiv : 1212.1724 . дои : 10.1016/j.jctb.2015.12.009 .
^ Бачик Р.; Махаджан, С. (1995). «Полуопределенное программирование и его приложения к задачам NP». Вычисления и комбинаторика . Конспекты лекций по информатике. Том. 959. с. 566. дои : 10.1007/BFb0030878 . ISBN 978-3-540-60216-3 .
^ Домашний продукт ^[2] является графическим дополнением гомоморфного произведения. ^[1]

Ссылки

Имрих, Вильфрид; Клавжар, Санди (2000). Графики продуктов: структура и узнаваемость . Уайли. ISBN 978-0-471-37039-0 .

[rm12-1] Jump up to: ^а ^б Роберсон, Дэвид Э.; Манчинска, Лаура (2012). «Гомоморфизмы графов для квантовых игроков». Журнал комбинаторной теории, серия B. 118 : 228–267. arXiv : 1212.1724 . дои : 10.1016/j.jctb.2015.12.009 .

[2] Бачик Р.; Махаджан, С. (1995). «Полуопределенное программирование и его приложения к задачам NP». Вычисления и комбинаторика . Конспекты лекций по информатике. Том. 959. с. 566. дои : 10.1007/BFb0030878 . ISBN 978-3-540-60216-3 .

[3] Домашний продукт ^[2] является графическим дополнением гомоморфного произведения. ^[1]

[1]

[3]

[2]