Уникально раскрашиваемый график
В теории графов однозначно раскрашиваемый граф — это k -хроматический граф , имеющий только одну возможную (правильную) k - раскраску с точностью до перестановки цветов. Эквивалентно, есть только один способ разбить его вершины на k независимых наборов , и нет способа разбить их на k - 1 независимых наборов.
Примеры
[ редактировать ]раскрашивается Полный граф однозначно, поскольку единственная правильная раскраска — это та, которая присваивает каждой вершине свой цвет.
Каждое k -дерево однозначно ( k + 1)-раскрашиваемо. что однозначно раскрашиваемые в 4 плоские графы Известно, представляют собой именно аполлоновы сети , то есть плоские 3-деревья. [1]
Любой связный двудольный граф однозначно раскрашивается в 2 цвета. Его 2-раскраску можно получить, выбрав произвольную начальную вершину, раскрасив вершины на четном расстоянии от начальной вершины одним цветом и раскрасив вершины на нечетном расстоянии от начальной вершины другим цветом. [2]
Характеристики
[ редактировать ]Некоторые свойства однозначно k -раскрашиваемого графа G с n вершинами и m ребрами:
- m ≥ ( k - 1) n - k ( k -1)/2. [3]
Связанные понятия
[ редактировать ]Минимальное несовершенство
[ редактировать ]Минимальный несовершенный граф — это граф, в котором каждый подграф совершенен . Удаление любой вершины из минимального несовершенного графа оставляет подграф, который можно раскрасить однозначно.
Уникальная возможность окрашивания кромок
[ редактировать ]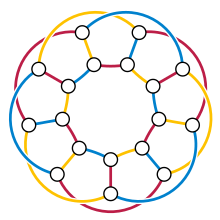
Граф , однозначно раскрашиваемый по ребрам, — это граф с k -ребрами , который имеет только одну возможную (правильную) раскраску k -ребер с точностью до перестановки цветов. Единственными графами, которые можно однозначно раскрасить в 2 ребра, являются пути и циклы. Для любого k звезды -раскрашиваемы K 1, k однозначно k . Более того, Уилсон (1976) предположил, а Томасон (1978) доказал, что при k ≥ 4 они также являются единственными членами этого семейства. Однако существуют графы, однозначно раскрашиваемые в 3 ребра, которые не вписываются в эту классификацию, например граф треугольной пирамиды .
Если кубический граф однозначно раскрашивается в 3-ребра, он должен иметь ровно три гамильтоновых цикла , образованных ребрами двух из трех цветов, но некоторые кубические графы только с тремя гамильтоновыми циклами не являются однозначно раскрашиваемыми в 3-ребра. [4] Каждый простой планарный кубический граф, который однозначно раскрашивается в 3 ребра, содержит треугольник, [1] но WT Tutte ( 1976 ) заметил, что обобщенный граф Петерсена G (9,2) неплоский , не содержит треугольников и однозначно раскрашивается в 3 ребра. В течение многих лет это был единственный известный такой граф, и предполагалось, что это единственный такой граф. [5] но теперь известно бесконечно много неплоских кубических графов без треугольников, однозначно раскрашиваемых в 3 ребра. [6]
Уникальная полная возможность окрашивания
[ редактировать ]Единственно тотальный раскрашиваемый граф — это k -тотально-хроматический граф , который имеет только одну возможную (правильную) k -тотальную раскраску с точностью до перестановки цветов.
Пустые графы , пути и циклы длины, кратной 3, являются однозначно полными раскрашиваемыми графами. Махмудиан и Шокроллахи (1995) предположили, что они также являются единственными членами этой семьи.
Некоторые свойства однозначно k -тотально раскрашиваемого графа G с n вершинами:
Здесь χ″( G ) — полное хроматическое число ; Δ( G ) – максимальная степень ; и δ( G ) — минимальная степень .
Примечания
[ редактировать ]Ссылки
[ редактировать ]- Акбари, С. (2003), «Две гипотезы об однозначно полностью раскрашиваемых графах», Discrete Mathematics , 266 (1–3): 41–45, doi : 10.1016/S0012-365X(02)00797-5 , MR 1991705 .
- Акбари, С.; Бехзад, М.; Хаджиаболхассан, Х.; Махмудян, ES (1997), «Однозначно полные раскрашиваемые графы», Graphs and Combinatorics , 13 (4): 305–314, doi : 10.1016/S0012-365X(02)00797-5 , MR 1485924 .
- Белькастро, Сара-Мари ; Хаас, Рут (2015), «Кубические графы, однозначно раскрашиваемые с 3 ребрами, без треугольников», Вклад в дискретную математику , 10 (2): 39–44, arXiv : 1508.06934 , doi : 10.11575/cdm.v10i2.62320 , MR 3499076 .
- Боллобас, Бела (1978), Экстремальная теория графов , Монографии LMS, том. 11, Академик Пресс, МР 0506522 .
- Фаулер, Томас (1998), Уникальная раскраска планарных графов (PDF) , доктор философии. диссертация, математический факультет Технологического института Джорджии .
- Хиллар, Кристофер Дж.; Виндфельдт, Троэлс (2008), «Алгебраическая характеристика однозначно раскрашиваемых вершин», Журнал комбинаторной теории , серия B, 98 (2): 400–414, arXiv : math/0606565 , doi : 10.1016/j.jctb.2007.08. 004 , МР 2389606 , S2CID 108304 .
- Махмудян, ES (1998), «Определение множеств и уникальности в раскрасках графов: обзор», Journal of Statistical Planning and Inference , 73 (1–2): 85–89, doi : 10.1016/S0378-3758(98)00053- 6 , МР 1655213 .
- Махмудян, Э.С.; Шокроллахи, Массачусетс (1995), «Открытые проблемы на семинаре по комбинаторике AIMC25 (Тегеран, 1994)», в CJ, Колборн ; ES, Махмудиан (ред.), Достижения комбинаторики , Математика и ее приложения, том. 329, Дордрехт; Бостон; Лондон: Kluwer Academic Publishers, стр. 321–324 .
- Швенк, Аллен Дж. (1989), «Перечисление гамильтоновых циклов в некоторых обобщенных графах Петерсена», Журнал комбинаторной теории , серия B, 47 (1): 53–59, doi : 10.1016/0095-8956(89)90064- 6 , МР 1007713 .
- Томасон, А.Г. (1978), «Гамильтоновы циклы и графы, раскрашиваемые однозначно по краям», Достижения в теории графов (Кембриджская комбинаторная конференция, Тринити-колледж, Кембридж, 1977) , Анналы дискретной математики, том. 3, стр. 259–268, МР 0499124 .
- Томасон, Эндрю (1982), «Кубические графы с тремя гамильтоновыми циклами не всегда однозначно раскрашиваются по краям», Journal of Graph Theory , 6 (2): 219–221, doi : 10.1002/jgt.3190060218 , MR 0655209 .
- Трушинский, М. (1984), «Некоторые результаты об однозначно раскрашиваемых графах», в Хайнал, А .; Ловас, Л. ; Сос, В.Т. (ред.), Конечные и бесконечные множества. Том. Я, II. Материалы шестого венгерского комбинаторного коллоквиума, состоявшегося в Эгере 6–11 июля 1981 г. , Colloq. Математика. Соц. Янош Бояи, том. 37, Северная Голландия, Амстердам, стр. 733–748, MR 0818274 .
- Олл, Уильям Т. (1976), «Гамильтоновы схемы», Международный коллоквиум по комбинаторным теориям (Рим, 1973), Том I , Accad. Нат. Линчеи, Рим, стр. 193–199. Материалы Линцианских конференций, № 17, MR 0480185 . Цитируется Белкастро и Хаасом (2015) .
- Сюй, Шао Цзи (1990), «Размер однозначно раскрашиваемых графов», Журнал комбинаторной теории , серия B, 50 (2): 319–320, doi : 10.1016/0095-8956(90)90086-F , MR 1081235 .
- Уилсон, Р.Дж. (1976), «Проблема 2», в Нэш-Уильямсе, К.Ст.Дж.А .; Шиэн, Дж. (ред.), Proc. Британский гребень. Конф. 1975 , Виннипег: Utilitas Math., с. 696 . Цитируется Томасоном (1978) .