уравнение ЗФК

Уравнение ZFK , аббревиатура от уравнения Зельдовича-Франка-Каменецкого , представляет собой уравнение реакции-диффузии , которое моделирует распространение пламени предварительно смешанной смеси . Уравнение названо в честь Якова Зельдовича и Дэвида А. Франк-Каменецкого, которые вывели его в 1938 году, и также известно как уравнение Нагумо. ^[1]^[2] Уравнение аналогично уравнению КПП, за исключением того, что оно содержит экспоненциальное поведение для члена реакции и принципиально отличается от уравнения КПП в отношении скорости распространения бегущей волны. В безразмерной форме уравнение имеет вид

{\frac {\partial \theta }{\partial t}}={\frac {\partial ^{2}\theta }{\partial x^{2}}}+\omega (\theta )

с типичной формой для $\omega$ данный

\omega ={\frac {\beta ^{2}}{2}}\theta (1-\theta )e^{-\beta (1-\theta )}

где $\theta \in [0,1]$ - безразмерная зависимая переменная (обычно температура) и $\beta$ — число Зельдовича . В ЗФК режиме $\beta \gg 1$ . Уравнение сводится к уравнению Фишера для $\beta \ll 1$ и таким образом $\beta \ll 1$ соответствует режиму КПП . Минимальная скорость распространения $U_{min}$ (обычно это асимптотическая скорость при длительном времени) бегущей волны в режиме ZFK определяется выражением

U_{ZFK}\propto {\sqrt {2\int _{0}^{1}\omega (\theta )d\theta }}

тогда как в режиме KPP он определяется выражением

U_{KPP}=2{\sqrt {\left.{\frac {d\omega }{d\theta }}\right|_{\theta =0}}}.

Решение бегущей волны

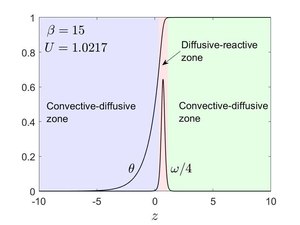
Подобно уравнению Фишера , для этой задачи можно найти решение бегущей волны. Предположим, что волна движется справа налево с постоянной скоростью. $U$ , то в координате, присоединенной к волне, т. е. $z=x+Ut$ , проблема становится устойчивой. Уравнение ЦФК сводится к

U{\frac {d\theta }{dz}}={\frac {d^{2}\theta }{dz^{2}}}+{\frac {\beta ^{2}}{2}}\theta (1-\theta )e^{-\beta (1-\theta )}

удовлетворяющие граничным условиям $\theta (-\infty )=0$ и $\theta (+\infty )=1$ . Граничные условия выполняются достаточно гладко, так что производная $d\theta /dz$ также исчезает, как $z\rightarrow \pm \infty$ . Поскольку уравнение трансляционно инвариантно относительно $z$ направление, дополнительное условие, скажем, например $\theta (0)=1/2$ , можно использовать для фиксации местоположения волны. Скорость волны $U$ получается как часть решения, образуя таким образом нелинейную проблему собственных значений. ^[3] Численное решение приведенного выше уравнения, $\theta$ , собственное значение $U$ и соответствующий член реакции $\omega$ показаны на рисунке, рассчитаны для $\beta =15$ .

Асимптотическое решение ^[4]

Режим ZFK как $\beta \rightarrow \infty$ формально анализируется с использованием асимптотики энергии активации . С $\beta$ большой, срок $e^{-\beta (1-\theta )}$ сделает член реакции практически нулевым, однако этим членом можно пренебречь, если $1-\theta \sim 1/\beta$ . Член реакции также будет равен нулю, если $\theta =0$ и $\theta =1$ . Поэтому ясно, что $\omega$ пренебрежимо мал всюду, кроме тонкого слоя вблизи правой границы $\theta =1$ . Таким образом, проблема разделена на три области: внутреннюю диффузионно-реактивную область, окруженную с обеих сторон двумя внешними конвективно-диффузионными областями.

Внешний регион

Задача для внешнего региона определяется выражением

U{\frac {d\theta }{dz}}={\frac {d^{2}\theta }{dz^{2}}}.

Решение, удовлетворяющее условию $\theta (-\infty )=0$ является $\theta =e^{Uz}$ . Это решение также сделано для удовлетворения $\theta (0)=1$ (произвольный выбор), чтобы зафиксировать положение волны где-то в области, поскольку задача трансляционно инвариантна в $z$ направление. Как $z\rightarrow 0^{-}$ , внешнее решение ведет себя как $\theta =1+Uz+\cdots$ что, в свою очередь, подразумевает $d\theta /dz=U+\cdots .$

Решение, удовлетворяющее условию $\theta (+\infty )=1$ является $\theta =1$ . Как $z\rightarrow 0^{+}$ , внешнее решение ведет себя как $\theta =1$ и таким образом $d\theta /dz=0$ .

Мы видим это, хотя $\theta$ является непрерывным в $z=0$ , $d\theta /dz$ прыгает на $z=0$ . Переход между производными описывается внутренней областью.

Внутренний регион

Во внутренней области, где $1-\theta \sim 1/\beta$ , срок реакции уже не является незначительным. Для исследования структуры внутреннего слоя вводится растянутая координата, охватывающая точку $z=0$ потому что именно там $\theta$ приближается к единице по внешнему решению и растянутой зависимой переменной по $\eta =\beta z,\,\Theta =\beta (1-\theta ).$ Подставив эти переменные в основное уравнение и собрав только члены старшего порядка, мы получаем

2{\frac {d^{2}\Theta }{d\eta ^{2}}}=\Theta e^{-\Theta }.

Граничное условие как $\eta \rightarrow -\infty$ происходит из локального поведения внешнего решения, полученного ранее, которое, когда мы записываем в терминах координаты внутренней зоны, становится $\Theta \rightarrow -U\eta =+\infty$ и $d\Theta /d\eta =-U$ . Аналогично, как $\eta \rightarrow +\infty$ . мы находим $\Theta =d\Theta /d\eta =0$ . Первый интеграл приведенного выше уравнения после наложения этих граничных условий становится

{\begin{aligned}\left.\left({\frac {d\Theta }{d\eta }}\right)^{2}\right|_{\Theta =\infty }-\left.\left({\frac {d\Theta }{d\eta }}\right)^{2}\right|_{\Theta =0}&=\int _{0}^{\infty }\Theta e^{-\Theta }d\Theta \\U^{2}&=1\end{aligned}}

что подразумевает $U=1$ . Из первого интеграла ясно, что квадрат скорости волны $U^{2}$ пропорциональна интегрированному (по отношению к $\theta$ ) значение $\omega$ (разумеется, в большом $\beta$ пределе, вклад в этот интеграл вносит только внутренняя зона). Первый интеграл после замены $U=1$ дается

{\frac {d\Theta }{d\eta }}=-{\sqrt {1-(\Theta +1)\exp(-\Theta )}}.

Переход КПП – ЗФК

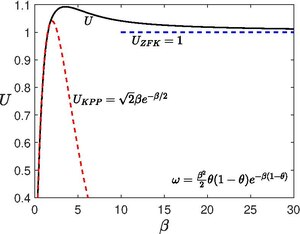
В режиме КПП $U_{min}=U_{KPP}.$ Для используемого здесь термина реакции скорость КПП, применимая для $\beta \ll 1$ дается ^[5]

U_{KPP}=2{\sqrt {\left.{\frac {d\omega }{d\theta }}\right|_{\theta =0}}}={\sqrt {2}}\beta e^{-\beta /2}

тогда как в режиме ЗФК, как мы видели выше $U_{ZFK}=1$ . Численное интегрирование уравнения для различных значений $\beta$ показал, что существует критическое значение $\beta _{*}=1.64$ такой, что только для $\beta \leq \beta _{*}$ , $U_{min}=U_{KPP}.$ Для $\beta \geq \beta _{*}$ , $U_{min}$ больше, чем $U_{KPP}$ . Как $\beta \gg 1$ , $U_{min}$ подходы $U_{ZFK}=1$ тем самым приближаясь к режиму ZFK. Область между режимом КПП и режимом ЗФК называется переходной зоной КПП-ЗФК.

Критическое значение зависит от модели реакции, например, получаем

\beta _{*}=3.04\quad {\text{for}}\quad \omega \propto (1-\theta )e^{-\beta (1-\theta )}

\beta _{*}=5.11\quad {\text{for}}\quad \omega \propto (1-\theta )^{2}e^{-\beta (1-\theta )}.

Модель Клавина – Линьяна

Чтобы аналитически предсказать переход KPP-ZFK, Пол Клавин и Амабэль Линьян предложили простую кусочно-линейную модель. ^[6]

\omega (\theta )={\begin{cases}\theta \quad {\text{if}}\quad 0\leq \theta \leq 1-\epsilon ,\\h(1-\theta )/\epsilon ^{2}\quad {\text{if}}\quad 1-\epsilon \leq \theta \leq 1\end{cases}}

где $h$ и $\epsilon$ являются константами. Скорость КПП модели равна $U_{KPP}=2$ , тогда как скорость ZFK получается как $U_{ZFK}={\sqrt {h}}$ в двойном лимите $\epsilon \rightarrow 0$ и $h\rightarrow \infty$ что имитирует резкое усиление реакции вблизи $\theta =1$ .

Для этой модели существует критическое значение $h_{*}=1-\epsilon ^{2}$ такой, что

{\begin{cases}h<h_{*}:&\quad U_{min}=U_{KPP},\\h>h_{*}:&\quad U_{min}={\frac {h/(1-\epsilon )+1-\epsilon }{\sqrt {h/(1-\epsilon )-\epsilon }}},\\h\gg h_{*}:&\quad U_{min}\rightarrow U_{ZFK}\end{cases}}

См. также

Уравнение Фишера

Ссылки

^ Зельдович Ю.Б. и Франк-Каменецкий Д.А. (1938). Теория теплового распространения пламени. Ж. Физ. Хим, 12, 100-105.
^ Бикташев В.Н.; Идрис, И. (2008). «Инициирование волн возбуждения: аналитический подход» . 2008 Компьютеры в кардиологии . стр. 311–314. дои : 10.1109/CIC.2008.4749040 . ISBN 978-1-4244-3706-1 . S2CID 15607806 .
^ Эванс, LC (2010). Уравнения в частных производных (Том 19). Американское математическое соц.
^ Уильямс, ФА (2018). Теория горения. ЦРК Пресс.
^ Клавин П. и Сирби Г. (2016). Волны и фронты горения в потоках: пламя, ударные толчки, детонации, фронты абляции и взрывы звезд. Издательство Кембриджского университета.
^ Клавин П. и Линьян А. (1984). Теория газового горения. В книге «Неравновесные кооперативные явления в физике и смежных областях» (стр. 291–338). Спрингер, Бостон, Массачусетс.

[1] Зельдович Ю.Б. и Франк-Каменецкий Д.А. (1938). Теория теплового распространения пламени. Ж. Физ. Хим, 12, 100-105.

[2] Бикташев В.Н.; Идрис, И. (2008). «Инициирование волн возбуждения: аналитический подход» . 2008 Компьютеры в кардиологии . стр. 311–314. дои : 10.1109/CIC.2008.4749040 . ISBN 978-1-4244-3706-1 . S2CID 15607806 .

[3] Эванс, LC (2010). Уравнения в частных производных (Том 19). Американское математическое соц.

[4] Уильямс, ФА (2018). Теория горения. ЦРК Пресс.

[5] Клавин П. и Сирби Г. (2016). Волны и фронты горения в потоках: пламя, ударные толчки, детонации, фронты абляции и взрывы звезд. Издательство Кембриджского университета.

[6] Клавин П. и Линьян А. (1984). Теория газового горения. В книге «Неравновесные кооперативные явления в физике и смежных областях» (стр. 291–338). Спрингер, Бостон, Массачусетс.

[1]

[2]

[3]

[4]

[5]

[6]