Код стирания

В теории кодирования — код стирания это код прямого исправления ошибок (FEC) в предположении стирания битов (а не битовых ошибок), который преобразует сообщение из k символов в более длинное сообщение (кодовое слово) с n символами так, что исходное сообщение может быть восстановлено из подмножества n символов. Дробь r = k / n называется скоростью кода . Дробь k'/k , где k' обозначает количество символов, необходимое для восстановления, называется эффективностью приема . Алгоритм восстановления предполагает, что известно, какой из n символов потерян — в отличие от кодов прямого исправления ошибок .

История

Стирающее кодирование было изобретено Ирвингом Ридом и Гюставом Соломоном в 1960 году. ^[1]

Существует множество различных схем стирающего кодирования. Наиболее популярные коды стирания: кодирование Рида-Соломона , Код проверки четности низкой плотности (коды LDPC) и Турбокоды . ^[1]

По состоянию на 2023 год современные системы хранения данных могут быть спроектированы так, чтобы выдерживать полный выход из строя нескольких дисков без потери данных, используя один из трех подходов: ^[2]^[3]^[4]

Репликация
Рейд
Стирающее кодирование

Хотя технически RAID можно рассматривать как своего рода стирающий код, ^[5] «RAID» обычно применяется к массиву, подключенному к одному главному компьютеру (который является единственной точкой отказа), тогда как «стирающее кодирование» обычно подразумевает несколько хостов. ^[3] иногда называемый избыточным массивом недорогих серверов (RAIS). Код стирания позволяет операциям продолжаться, когда любой из этих хостов останавливается. ^[4]^[6]

По сравнению с RAID-системами на уровне блоков кодирование стирания объектных хранилищ имеет некоторые существенные различия, которые делают его более устойчивым. ^[7]^[8]^[9]^[10]^[11]

Оптимальные коды стирания

Оптимальные стирающие коды обладают тем свойством, что любых k из n символов кодового слова достаточно для восстановления исходного сообщения (т. е. они имеют оптимальную эффективность приема). Оптимальными стирающими кодами являются коды, разделяемые на максимальное расстояние (MDS-коды).

Проверка четности

Проверка четности — это особый случай, когда n = k + 1. Из набора из k значений $\{v_{i}\}_{1\leq i\leq k}$ , контрольная сумма вычисляется и добавляется к исходным значениям k :

v_{k+1}=-\sum _{i=1}^{k}v_{i}.

Набор из k + 1 значений $\{v_{i}\}_{1\leq i\leq k+1}$ теперь согласован в отношении контрольной суммы. Если одно из этих значений, $v_{e}$ , стирается, его легко восстановить, суммируя оставшиеся переменные:

v_{e}=-\sum _{i=1,i\neq e}^{k+1}v_{i}.

RAID 5 — это широко используемое применение кода стирания проверки четности. ^[1]

Полиномиальная передискретизация

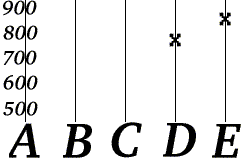
Пример: сообщение об ошибке ( k = 2)

В простом случае, когда k = 2, избыточные символы могут быть созданы путем выборки различных точек вдоль линии между двумя исходными символами. Это показано на простом примере под названием err-mail:

Алиса хочет отправить свой номер телефона (555629) Бобу по электронной почте. Err-mail работает так же, как и электронная почта, за исключением

Около половины всей почты теряется. ^[12]
Сообщения длиной более 5 символов являются незаконными.
Это очень дорого (аналогично авиапочте).

Вместо того, чтобы просить Боба подтвердить отправленные ею сообщения, Алиса придумывает следующую схему.

Она разбивает свой номер телефона на две части a = 555, b = 629 и отправляет Бобу два сообщения – «A=555» и «B=629».
Она строит линейную функцию, $f(i)=a+(b-a)(i-1)$ , в этом случае $f(i)=555+74(i-1)$ , такой, что $f(1)=555$ и $f(2)=629$ .

Она вычисляет значения f (3), f (4) и f (5), а затем передает три избыточных сообщения: «C=703», «D=777» и «E=851».

Боб знает, что форма f ( k ) есть $f(i)=a+(b-a)(i-1)$ , где a и b — две части телефонного номера. Теперь предположим, что Боб получает «D=777» и «E=851».

Боб может восстановить номер телефона Алисы, вычислив значения a и b значений ( f (4) и f на основе полученных им (5)). Боб может выполнить эту процедуру, используя любые два сообщения об ошибке, поэтому вероятность стирания кода в этом примере составляет 40%.

Обратите внимание, что Алиса не может закодировать свой номер телефона только в одном сообщении об ошибке, поскольку оно содержит шесть символов, а максимальная длина одного сообщения об ошибке составляет пять символов. Если бы она отправила свой номер телефона по частям, прося Боба подтвердить получение каждого фрагмента, в любом случае пришлось бы отправить как минимум четыре сообщения (два от Алисы и два подтверждения от Боба). Таким образом, код стирания в этом примере, требующий пяти сообщений, весьма экономичен.

Этот пример немного надуман. Для действительно общих кодов стирания, которые работают с любым набором данных, нам понадобится что-то иное, чем заданное f ( i ).

Общий случай

Линейную конструкцию, приведенную выше, можно обобщить до полиномиальной интерполяции . Кроме того, точки теперь вычисляются по конечному полю .

Сначала мы выбираем конечное поле F порядка не менее n , но обычно степени 2. Отправитель нумерует символы данных от 0 до k − 1 и отправляет их. Затем он строит полином (Лагранжа) p ( x ) порядка k такой, что p ( i ) равен символу данных i . Затем он отправляет p ( k ), ..., p ( n − 1). Получатель теперь также может использовать полиномиальную интерполяцию для восстановления потерянных пакетов при условии, что он успешно получит k символов. Если порядок F меньше 2 ^б, где b — количество битов в символе, то можно использовать несколько полиномов.

Отправитель может создавать символы от k до n − 1 «на лету», т. е. равномерно распределять рабочую нагрузку между передачей символов. Если получатель хочет выполнить свои вычисления «на лету», он может построить новый полином q , такой, что q ( i ) = p ( i ), если символ i < k был получен успешно, и q ( i ) = 0, когда символ i < k не было получено. Теперь пусть р ( я ) = п ( я ) - q ( я ). Во-первых, мы знаем, что r ( i ) = 0, если символ i < k был получен успешно. Во-вторых, если символ i ≥ k был получен успешно, то r ( i ) = p ( i ) − q ( i можно вычислить ). Итак, у нас достаточно точек данных, чтобы построить r и оценить его, чтобы найти потерянные пакеты. Таким образом, и отправителю, и получателю требуется O ( n ( n - k )) операций и только O ( n - k ) пространства для работы «на лету».

Реализация в реальном мире

Этот процесс реализуется кодами Рида-Соломона с кодовыми словами, построенными над конечным полем с использованием матрицы Вандермонда .

Наиболее практичными кодами стирания являются систематические коды : каждый из исходных k символов можно найти скопированным в незакодированном виде как один из n символов сообщения. ^[13] (Коды стирания, поддерживающие обмен секретами , никогда не используют систематический код).

Почти оптимальные коды стирания

Почти оптимальные коды стирания требуют (1 + ε) k символов для восстановления сообщения (где ε>0). Уменьшение ε можно сделать за счет процессорного времени. Почти оптимальные стирающие коды обменивают возможности коррекции на вычислительную сложность: практические алгоритмы могут кодировать и декодировать с линейной временной сложностью.

Фонтанные коды (также известные как коды стирания без скорости ) являются яркими примерами почти оптимальных кодов стирания . Они могут преобразовать сообщение k -символов в практически бесконечную закодированную форму, т. е. они могут генерировать произвольное количество избыточных символов, которые все можно использовать для исправления ошибок. Получатели могут начать декодирование после того, как они получили чуть больше k закодированных символов.

Регенерация кодов решает проблему восстановления (также называемого восстановлением) потерянных закодированных фрагментов из существующих закодированных фрагментов. Эта проблема возникает в распределенных системы хранения, в которых связь для поддержания избыточности кодирования является проблемой. ^[13]

Применение стирающего кодирования в системах хранения данных

Стирающее кодирование теперь является стандартной практикой для надежного хранения данных. ^[14]^[15]^[16] В частности, различные реализации стирающего кодирования Рида-Соломона используются Apache Hadoop , RAID-6, встроенным в Linux, Microsoft Azure, холодным хранилищем Facebook и Backblaze Vaults. ^[16]^[13]

Классическим способом восстановления после сбоев в системах хранения было использование репликации. Однако репликация сопряжена со значительными накладными расходами в виде потраченных впустую байтов. Поэтому все более крупные системы хранения, например те, которые используются в центрах обработки данных, используют хранилище со стирающим кодом. Наиболее распространенной формой стирающего кодирования, используемой в системах хранения, является код Рида-Соломона (RS) , усовершенствованная математическая формула, используемая для восстановления недостающих данных из частей известных данных, называемых блоками четности. В коде RS ( k , m ) заданный набор из k блоков данных, называемых «фрагментами», кодируется в ( k + m ) фрагментов. Общий набор чанков представляет собой полосу . Кодирование выполняется таким образом, что, пока доступно хотя бы k из ( k + m ) фрагментов, можно восстановить все данные. Это означает, что хранилище ( k , m ) с RS-кодированием может выдержать до m сбоев.

Пример: В коде RS (10, 4), который используется в Facebook для HDFS , ^[17] 10 МБ пользовательских данных разделены на десять блоков по 1 МБ. Затем создаются четыре дополнительных блока четности по 1 МБ для обеспечения избыточности. Это может допустить до 4 одновременных сбоев. Накладные расходы на хранение здесь составляют 14/10 = 1,4X.

В случае полностью реплицированной системы 10 МБ пользовательских данных придется реплицировать 4 раза, чтобы выдержать до 4 одновременных сбоев. Накладные расходы на хранение в этом случае составят 50/10 = 5 раз.

Это дает представление о меньших затратах на хранение при использовании хранилища со стирающим кодом по сравнению с полной репликацией и, следовательно, о привлекательности современных систем хранения.

Первоначально коды стирания использовались для эффективного снижения стоимости хранения «холодных» (редко доступных) данных; но коды стирания также можно использовать для повышения производительности при обработке «горячих» (более часто используемых) данных. ^[13]

RAID N+M разделяет блоки данных по дискам N+M и может восстановить все данные в случае сбоя любого из дисков M. ^[1] В частности, RAID 7.3 относится к RAID с тройной четностью и может восстановить все данные при выходе из строя любых трех дисков. ^[18]

Примеры

Вот несколько примеров реализации различных кодов:

Почти оптимальные коды стирания

Почти оптимальные коды фонтанного (бесскоростного стирания)

Оптимальные коды стирания

Четность : используется в RAID . системах хранения
архив
Tahoe-LAFS включает zfec
Коды Рида – Соломона
Erasure Resilient Systematic Code — код MDS, превосходящий Рида-Соломона по максимальному количеству избыточных пакетов. ^{[ по мнению кого? ]} см. RS(4,2) с 2 битами или RS(9,2) с 3 битами.
Регенерация кодов ^[19]^[20]
любой другой код, разделяемый на максимальное расстояние

См. также

Коды прямого исправления ошибок .
Совместное использование секрета (отличается тем, что исходный секрет шифруется и скрывается до тех пор, пока не будет достигнут кворум декодирования)
Орфографический алфавит

Ссылки

^ Jump up to: ^а ^б ^с ^д «RAID и стирающее кодирование. Какая разница?» .
^ "Стирающее кодирование в Ceph" .
^ Jump up to: ^а ^б «RAID, стирающее кодирование и репликация» .
^ Jump up to: ^а ^б Джим О'Рейли. «RAID против стирающего кодирования» .
^ Дмитрий Пертен, Александр ван Кемпен, Бенуа Паррен, Николя Норманд. «Сравнение кодов стирания RAID-6» . Третий китайско-французский семинар по информационным и коммуникационным технологиям, SIFWICT 2015, июнь 2015 г., Нант, Франция. ffhal-01162047f
^ ""
^ «Кодирование стирания объектного хранилища или RAID блочного хранилища» .
^ «Стирающее кодирование против Raid как метод защиты данных» .
^ Питер Крут. «Код стирания: RAID, каким он должен быть» .
^ «Стирающее кодирование 101» .
^ «Почему стирающее кодирование — это будущее устойчивости данных» .
^ Некоторые версии этой истории относятся к демону err-mail.
^ Jump up to: ^а ^б ^с ^д Рашми Винаяк. «Стирающее кодирование для систем больших данных: теория и практика» . 2016. п. 2: раздел «Реферат». п. 9: раздел «Систематические коды». п. 12: раздел «Регенерация кодов».
^ «Стирающее кодирование — практика и принципы» . 2016.
^ Мэтт Саррел. «Стирающее кодирование 101» . 2022.
^ Jump up to: ^а ^б Брайан Бич. «Исходный код стирающего кодирования Рида-Соломона с открытым исходным кодом Backblaze» . 2015.
^ Ся, Минъюань; Саксена, Мохит; Блаум, Марио; Пиз, Дэвид А. (2015). История о двух стирающих кодах в {HDFS} . стр. 213–226. ISBN 978-1-931971-20-1 .
^ Адам Левенталь. "" RAID с тройной четностью и не только" . 2009.
^ Димакис, Александрос Г.; Годфри, П. Брайтен; Ву, Юньнань; Уэйнрайт, Мартин Дж.; Рамчандран, Каннан (сентябрь 2010 г.). «Сетевое кодирование для распределенных систем хранения». Транзакции IEEE по теории информации . 56 (9): 4539–4551. arXiv : cs/0702015 . CiteSeerX 10.1.1.117.6892 . дои : 10.1109/TIT.2010.2054295 . S2CID 260559901 .
^ "home [Erasure Coding for Distributed Storage Wiki]" . 2017-07-31. Архивировано из оригинала 31 июля 2017 г. Проверено 20 августа 2023 г.

Внешние ссылки

Jerasure — это библиотека бесплатного программного обеспечения, реализующая методы стирания кода Рида-Соломона и Коши с оптимизацией SIMD.
Программное обеспечение FEC в компьютерных коммуникациях Луиджи Риццо описывает оптимальные коды коррекции стирания.
Feclib — это почти оптимальное расширение работы Луиджи Риццо, в котором используются ленточные матрицы. Можно установить множество параметров, таких как размер ширины полосы и размер конечного поля. Он также успешно использует большой размер регистров современных процессоров. Неизвестно, как он соотносится с почти оптимальными кодами, упомянутыми выше.
Вики-сайт «Кодирование для распределенного хранилища» для регенерации кодов и восстановления кодов стирания.
ECIP «Интернет-протокол стирания кода», разработанный в 1996 году, стал первым использованием FEC «прямого исправления ошибок» в Интернете. Впервые он был использован в коммерческих целях для потоковой передачи живого видео сэра Артура Кларка в Шри-Ланке на UIUC в Индиане .

[xinnor-1] Jump up to: ^а ^б ^с ^д «RAID и стирающее кодирование. Какая разница?» .

[2] "Стирающее кодирование в Ceph" .

[bdr-3] Jump up to: ^а ^б «RAID, стирающее кодирование и репликация» .

[jor-4] Jump up to: ^а ^б Джим О'Рейли. «RAID против стирающего кодирования» .

[5] Дмитрий Пертен, Александр ван Кемпен, Бенуа Паррен, Николя Норманд. «Сравнение кодов стирания RAID-6» . Третий китайско-французский семинар по информационным и коммуникационным технологиям, SIFWICT 2015, июнь 2015 г., Нант, Франция. ffhal-01162047f

[6] ""

[7] «Кодирование стирания объектного хранилища или RAID блочного хранилища» .

[8] «Стирающее кодирование против Raid как метод защиты данных» .

[9] Питер Крут. «Код стирания: RAID, каким он должен быть» .

[10] «Стирающее кодирование 101» .

[11] «Почему стирающее кодирование — это будущее устойчивости данных» .

[12] Некоторые версии этой истории относятся к демону err-mail.

[vinayak-13] Jump up to: ^а ^б ^с ^д Рашми Винаяк. «Стирающее кодирование для систем больших данных: теория и практика» . 2016. п. 2: раздел «Реферат». п. 9: раздел «Систематические коды». п. 12: раздел «Регенерация кодов».

[14] «Стирающее кодирование — практика и принципы» . 2016.

[15] Мэтт Саррел. «Стирающее кодирование 101» . 2022.

[bbeach-16] Jump up to: ^а ^б Брайан Бич. «Исходный код стирающего кодирования Рида-Соломона с открытым исходным кодом Backblaze» . 2015.

[17] Ся, Минъюань; Саксена, Мохит; Блаум, Марио; Пиз, Дэвид А. (2015). История о двух стирающих кодах в {HDFS} . стр. 213–226. ISBN 978-1-931971-20-1 .

[18] Адам Левенталь. "" RAID с тройной четностью и не только" . 2009.

[regcodes-19] Димакис, Александрос Г.; Годфри, П. Брайтен; Ву, Юньнань; Уэйнрайт, Мартин Дж.; Рамчандран, Каннан (сентябрь 2010 г.). «Сетевое кодирование для распределенных систем хранения». Транзакции IEEE по теории информации . 56 (9): 4539–4551. arXiv : cs/0702015 . CiteSeerX 10.1.1.117.6892 . дои : 10.1109/TIT.2010.2054295 . S2CID 260559901 .

[20] "home [Erasure Coding for Distributed Storage Wiki]" . 2017-07-31. Архивировано из оригинала 31 июля 2017 г. Проверено 20 августа 2023 г.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]