Треугольник Фюрмана

Треугольник Фюрмана (красный): $\triangle M_{c}^{\prime }M_{b}^{\prime }M_{a}^{\prime }$
средние точки дуги: $M_{a},M_{b},M_{c}$

Треугольник Фюрмана (красный): $\triangle M_{c}^{\prime }M_{b}^{\prime }M_{a}^{\prime }$
$\triangle M_{c}^{\prime }M_{b}^{\prime }M_{a}^{\prime }\sim \triangle M_{a}M_{b}M_{c}$

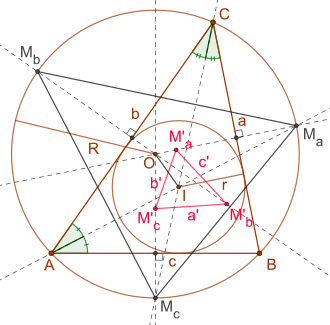
Треугольник Фюрмана , названный в честь Вильгельма Фюрмана (1833–1904), представляет собой особый треугольник, основанный на заданном произвольном треугольнике.

Для данного треугольника $\triangle ABC$ а окружность, описанную вокруг него , середины дуг над сторонами треугольника обозначим через $M_{a},M_{b},M_{c}$. Эти средние точки отражаются на связанных сторонах треугольника, образуя точки. $M_{a}^{\prime },M_{b}^{\prime },M_{c}^{\prime }$, который образует треугольник Фюрмана .

Описанная окружность треугольника Фурмана — это окружность Фурмана . Кроме того, треугольник Фурмана подобен треугольнику, образованному средними точками дуги, то есть $\triangle M_{c}^{\prime }M_{b}^{\prime }M_{a}^{\prime }\sim \triangle M_{a}M_{b}M_{c}$. Для площади треугольника Фюрмана справедлива следующая формула:

$|\triangle M_{c}^{\prime }M_{b}^{\prime }M_{a}^{\prime }|={\frac {(a+b+c)|OI|^{2}}{4R}}={\frac {(a+b+c)(R-2r)}{4}}$

Где $O$ обозначает центр описанной окружности данного треугольника $\triangle ABC$ и $R$ его радиус, а также $I$ обозначающий центр и $r$ его радиус. По теореме Эйлера также имеет место $|OI|^{2}=R(R-2r)$. Для сторон треугольника Фюрмана справедливы следующие уравнения:

$a^{\prime }={\sqrt {\frac {(-a+b+c)(a+b+c)}{bc}}}|OI|$

$b^{\prime }={\sqrt {\frac {(a-b+c)(a+b+c)}{ac}}}|OI|$

$c^{\prime }={\sqrt {\frac {(a+b-c)(a+b+c)}{ab}}}|OI|$

Где $a,b,c$ обозначим стороны данного треугольника $\triangle ABC$ и $a^{\prime },b^{\prime },c^{\prime }$ стороны треугольника Фюрмана (см. рисунок).