Регрессия-кригинг

В прикладной статистике и геостатистике регрессию регрессионный кригинг ( РК ) — это метод пространственного прогнозирования, который сочетает в себе зависимой переменной на вспомогательных переменных (таких как параметры, полученные в результате цифрового моделирования рельефа, дистанционного зондирования/изображений и тематических карт) с интерполяцией ( кригинг ) остатков регрессии. Он математически эквивалентен методу интерполяции, который по-разному называется универсальным кригингом и кригингом с внешним дрейфом , где вспомогательные предикторы используются непосредственно для определения весов кригинга. ^[1]

BLUP для пространственных данных

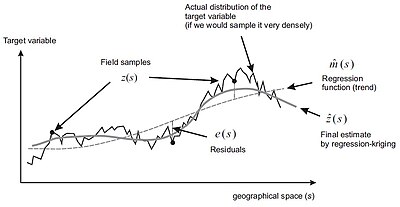
Регрессия-кригинг — это реализация лучшего линейного несмещенного предиктора (BLUP) для пространственных данных, т.е. лучшего линейного интерполятора, предполагающего универсальную модель пространственной вариации . Мэтерон (1969) предположил, что значение целевой переменной в некотором месте можно смоделировать как сумму детерминированного и стохастического компонентов: ^[2]

Z(\mathbf {s} )=m(\mathbf {s} )+\varepsilon '(\mathbf {s} )+\varepsilon ''

которую он назвал универсальной моделью пространственных вариаций . Как детерминированные , так и стохастические компоненты пространственных изменений можно моделировать отдельно. Объединив два подхода, получим:

{\hat {z}}(\mathbf {s} _{0})={\hat {m}}(\mathbf {s} _{0})+{\hat {e}}(\mathbf {s} _{0})=\sum \limits _{k=0}^{p}{{\hat {\beta }}_{k}\cdot q_{k}(\mathbf {s} _{0})}+\sum \limits _{i=1}^{n}\lambda _{i}\cdot e(\mathbf {s} _{i})

где ${\hat {m}}(\mathbf {s} _{0})$ - это подобранная детерминированная часть, ${\hat {e}}(\mathbf {s} _{0})$ интерполированная невязка, ${\hat {\beta }}_{k}$ – оцененные коэффициенты детерминированной модели ( ${\hat {\beta }}_{0}$ предполагаемый перехват), $\lambda _{i}$ – веса кригинга, определяемые структурой пространственной зависимости невязки, где $e(\mathbf {s} _{i})$ остаток в местоположении ${\mathbf {s} }_{i}$ . Коэффициенты регрессии ${\hat {\beta }}_{k}$ может быть оценено по выборке каким-либо методом подгонки, например, обычным методом наименьших квадратов (OLS) или, оптимально, с использованием обобщенного метода наименьших квадратов (GLS): ^[3]

\mathbf {\hat {\beta }} _{\mathtt {GLS}}=\left(\mathbf {q} ^{\mathbf {T} }\cdot \mathbf {C} ^{-\mathbf {1} }\cdot \mathbf {q} \right)^{-\mathbf {1} }\cdot \mathbf {q} ^{\mathbf {T} }\cdot \mathbf {C} ^{-\mathbf {1} }\cdot \mathbf {z}

где $\mathbf {\hat {\beta }} _{\mathtt {GLS}}$ – вектор оцененных коэффициентов регрессии, $\mathbf {C}$ - ковариационная матрица остатков, ${\mathbf {q} }$ представляет собой матрицу предикторов в местах отбора проб и $\mathbf {z}$ – вектор измеренных значений целевой переменной. Оценка коэффициентов регрессии GLS, по сути, является частным случаем географически взвешенной регрессии. В этом случае веса определяются объективно для учета пространственной автокорреляции между остатками.

После оценки детерминированной части вариации (регрессионной части) остаток можно интерполировать с помощью кригинга и добавить к предполагаемому тренду. Оценка остатков представляет собой итерационный процесс: сначала с помощью МНК оценивается детерминированная часть вариации, затем используется ковариационная функция остатков для получения коэффициентов GLS. Затем они используются для повторного расчета остатков, на основе которых вычисляется обновленная ковариационная функция и так далее. Хотя многие специалисты по геостатистике рекомендуют это как правильную процедуру, Китанидис (1994) показал, что использование ковариационной функции, полученной на основе остатков МНК (т.е. одной итерации), часто оказывается удовлетворительным, поскольку она недостаточно отличается от функции, полученной после нескольких итерации; т.е. это не сильно влияет на окончательные прогнозы. Минасни и МакБрэтни (2007) сообщают о схожих результатах: похоже, что использование большего количества данных более высокого качества важнее, чем использование более сложных статистических методов. ^[4]

В матричной записи регрессионный кригинг обычно записывается как: ^[5]

{\hat {z}}_{\mathtt {RK}}(\mathbf {s} _{0})=\mathbf {q} _{\mathbf {0} }^{\mathbf {T} }\cdot \mathbf {\hat {\beta }} _{\mathtt {GLS}}+\mathbf {\lambda } _{\mathbf {0} }^{\mathbf {T} }\cdot (\mathbf {z} -\mathbf {q} \cdot \mathbf {\hat {\beta }} _{\mathtt {GLS}})

где ${\hat {z}}({\mathbf {s} }_{0})$ прогнозируемое значение в местоположении ${\mathbf {s} }_{0}$ , ${\mathbf {q} }_{\mathbf {0} }$ вектор $p+1$ предикторы и $\mathbf {\lambda } _{\mathbf {0} }$ вектор $n$ веса кригинга, используемые для интерполяции остатков. Модель RK считается лучшим линейным предсказателем пространственных данных . ^[5]^[6] Он имеет дисперсию прогноза, которая отражает положение новых мест (экстраполяция) как в географическом, так и в пространстве объектов:

{\hat {\sigma }}_{\mathtt {RK}}^{2}(\mathbf {s} _{0})=(C_{0}+C_{1})-\mathbf {c} _{\mathbf {0} }^{\mathbf {T} }\cdot \mathbf {C} ^{-\mathbf {1} }\cdot \mathbf {c} _{\mathbf {0} }+\left(\mathbf {q} _{\mathbf {0} }-\mathbf {q} ^{\mathbf {T} }\cdot \mathbf {C} ^{-\mathbf {1} }\cdot \mathbf {c} _{\mathbf {0} }\right)^{\mathbf {T} }\cdot \left(\mathbf {q} ^{\mathbf {T} }\cdot \mathbf {C} ^{-\mathbf {1} }\cdot \mathbf {q} \right)^{\mathbf {-1} }\cdot \left(\mathbf {q} _{\mathbf {0} }-\mathbf {q} ^{\mathbf {T} }\cdot \mathbf {C} ^{-\mathbf {1} }\cdot \mathbf {c} _{\mathbf {0} }\right)

где $C_{0}+C_{1}$ - это изменение порога и ${\mathbf {c} }_{0}$ — вектор ковариаций остатков в непосещенном местоположении.

Многие (гео)статистики полагают, что существует только одна модель наилучшего линейного несмещенного прогнозирования для пространственных данных (например, регрессионный кригинг), все остальные методы, такие как обычный кригинг, корреляция с окружающей средой, усреднение значений на полигоны или обратная интерполяция расстояний, можно рассматривать как свои частные случаи. Если остатки не демонстрируют пространственной автокорреляции (чистый эффект самородка), регрессионный кригинг сходится к чистой множественной линейной регрессии, поскольку ковариационная матрица ( $\mathbf {C}$ ) становится единичной матрицей. Аналогично, если целевая переменная не показывает корреляции со вспомогательными предикторами, модель регрессионного кригинга сводится к обычной модели кригинга, поскольку детерминированная часть равна (глобальному) среднему значению. Следовательно, чистый кригинг и чистую регрессию следует рассматривать лишь как частные случаи регрессионного кригинга (см. рисунок).

РК и Великобритания/KED

В геостатистической литературе используется множество различных терминов для обозначения, по сути, одних и тех же или, по крайней мере, очень похожих методов. Это сбивает с толку пользователей и отвлекает их от использования правильной техники для картографических проектов. По сути, и универсальный кригинг, и кригинг с внешним дрейфом, и регрессионный кригинг — это, по сути, одна и та же техника.

Матерон (1969) первоначально назвал этот метод Le krigage Universel , однако этот метод был задуман как обобщенный случай кригинга, где тренд моделируется как функция координат. Таким образом, многие авторы оставляют термин универсальный кригинг (УК) для случая, когда в качестве предикторов используются только координаты. Если детерминированная часть вариации ( дрейф ) определяется извне как линейная функция некоторых вспомогательных переменных, а не координат, то термин кригинг с внешним дрейфом (KED) предпочтителен (согласно Хенглю, 2007, «О регрессионном кригинге: из уравнения для тематических исследований»). В случае UK или KED прогнозы делаются так же, как и при кригинге, с той разницей, что ковариационная матрица остатков расширяется за счет вспомогательных предикторов. Однако дрейф и остатки также можно оценить отдельно, а затем суммировать. Эта процедура была предложена Ахмедом и др. (1987) и Оде и др. (1995) позже назвали это регрессионным кригингом , а Гувертс (1997) использует термин кригинг с моделью тренда для обозначения семейства интерполяторов и называет RK простым кригингом с различными локальными средними значениями . Минасны и МакБрэтни (2007) называют этот метод просто «Эмпирический лучший линейный несмещенный предиктор», т.е. E-BLUP . ^[7]^[8]^[9]^[4]

В случае KED прогнозы в новых местах делаются посредством:

{\hat {z}}_{\mathtt {KED}}(\mathbf {s} _{0})=\sum \limits _{i=1}^{n}w_{i}^{\mathtt {KED}}(\mathbf {s} _{0})\cdot z(\mathbf {s} _{i})

для

\sum \limits _{i=1}^{n}w_{i}^{\mathtt {KED}}(\mathbf {s} _{0})\cdot q_{k}(\mathbf {s} _{i})=q_{k}(\mathbf {s} _{0})

для $k=1,\ldots ,p$ или в матричной записи:

{\hat {z}}_{\mathtt {KED}}(\mathbf {s} _{0})=\mathbf {\delta } _{\mathbf {0} }^{\mathbf {T} }\cdot \mathbf {z}

где $z$ целевая переменная, $q_{k}$ - это переменные-предикторы, т.е. значения в новом месте. $({\mathbf {s} }_{0})$ , ${\mathbf {\delta } }_{\mathbf {0} }$ – вектор весов KED ( $w_{i}^{\mathtt {KED}}$ ), $p$ количество предикторов и $\mathbf {z}$ вектор $n$ наблюдения в основных точках. Веса KED решаются с использованием расширенных матриц:

\mathbf {\lambda } _{\mathbf {0} }^{\mathtt {KED}}=\left\{w_{1}^{\mathtt {KED}}(\mathbf {s} _{0}),\ldots ,w_{n}^{\mathtt {KED}}(\mathbf {s} _{0}),\varphi _{0}(\mathbf {s} _{0}),\ldots ,\varphi _{p}(\mathbf {s} _{0})\right\}^{\mathbf {T} }=\mathbf {C} ^{{\mathtt {KED}}-1}\cdot \mathbf {c} _{\mathbf {0} }^{\mathtt {KED}}

где ${\mathbf {\lambda } }_{\mathbf {0} }^{\mathtt {KED}}$ вектор решаемых весов, $\varphi _{p}$ – множители Лагранжа, ${\mathbf {C} }^{\mathtt {KED}}$ расширенная ковариационная матрица остатков и ${\mathbf {c} }_{\mathbf {0} }^{\mathtt {KED}}$ — расширенный вектор ковариаций в новом месте.

В случае KED расширенная ковариационная матрица остатков выглядит следующим образом (Webster and Oliver, 2007; стр. 183): ^[10]

\mathbf {C} ^{\mathtt {KED}}=\left[{\begin{array}{ccccccc}C(\mathbf {s} _{1},\mathbf {s} _{1})&\cdots &C(\mathbf {s} _{1},\mathbf {s} _{n})&1&q_{1}(\mathbf {s} _{1})&\cdots &q_{p}(\mathbf {s} _{1})\\\vdots &&\vdots &\vdots &\vdots &&\vdots \\C(\mathbf {s} _{n},\mathbf {s} _{1})&\cdots &C(\mathbf {s} _{n},\mathbf {s} _{n})&1&q_{1}(\mathbf {s} _{n})&\cdots &q_{p}(\mathbf {s} _{n})\\1&\cdots &1&0&0&\cdots &0\\q_{1}(\mathbf {s} _{1})&\cdots &q_{1}(\mathbf {s} _{n})&0&0&\cdots &0\\\vdots &&\vdots &\vdots &\vdots &&\vdots \\q_{p}(\mathbf {s} _{1})&\cdots &q_{p}(\mathbf {s} _{n})&0&0&\cdots &0\end{array}}\right]

и $\mathbf {c} _{\mathbf {0} }^{\mathtt {KED}}$ так:

\mathbf {c} _{\mathbf {0} }^{\mathtt {KED}}=\left\{C(\mathbf {s} _{0},\mathbf {s} _{1}),\ldots ,C(\mathbf {s} _{0},\mathbf {s} _{n}),q_{0}(\mathbf {s} _{0}),q_{1}(\mathbf {s} _{0}),\ldots ,q_{p}(\mathbf {s} _{0})\right\}^{\mathbf {T} };q_{0}(\mathbf {s} _{0})=1

Следовательно, KED выглядит точно так же, как обычный кригинг, за исключением того, что ковариационная матрица/вектор расширена значениями вспомогательных предикторов.

Хотя на первый взгляд KED кажется более простым в вычислительном отношении, чем RK, параметры вариограммы KED также необходимо оценивать по остаткам регрессии, что требует отдельного этапа регрессионного моделирования. Эта регрессия должна быть GLS из-за вероятной пространственной корреляции между остатками. Обратите внимание, что многие аналитики вместо этого используют остатки OLS, которые могут не слишком отличаться от остатков GLS. Однако они не являются оптимальными, если существует какая-либо пространственная корреляция, и действительно, они могут сильно отличаться для кластеризованных точек выборки или если количество выборок относительно невелико ( $\ll 200$ ).

Ограничением KED является нестабильность расширенной матрицы в случае, когда ковариата не меняется плавно в пространстве. Преимущество RK заключается в том, что он явно отделяет оценку тренда от пространственного прогнозирования остатков, позволяя использовать произвольно сложные формы регрессии, а не простые линейные методы, которые можно использовать с KED. Кроме того, это позволяет раздельную интерпретацию двух интерполированных компонентов. Акцент на регрессии важен еще и потому, что подгонка детерминированной части вариации (регрессии) часто более полезна для качества окончательных карт, чем подгонка стохастической части (остатков).

Программное обеспечение для запуска регрессионного кригинга

Регрессионный кригинг можно автоматизировать, например, в среде статистических вычислений R , используя пакет gstat и/или geoR. Типичные входы/выходы включают в себя:

ВХОДЫ:

Набор интерполяции (карта точек) — $z(\mathbf {s} _{i})$ $i=1,\ldots ,n$ в основных местах;
Минимальные и максимальные ожидаемые значения и точность измерения ( $\Delta z$ );
Непрерывные предикторы (растровая карта) — $q(\mathbf {s} )$ ; в новых непосещенных локациях
Дискретные предикторы (полигональная карта);
Набор проверки (карта точек) — $z*(\mathbf {s} _{j})$ $j=1,\ldots ,l$ (необязательный);
Расстояние между лагами и предельное расстояние (необходимо для соответствия вариограмме);

ВЫХОДЫ:

Карта прогнозов и относительная ошибка прогноза;
Наилучшее подмножество предикторов и значимость корреляции (скорректированный R-квадрат);
Параметры модели вариограммы (например, $C_{0}$ , $C_{1}$ , $R$ )
коэффициенты модели дрейфа GLS;
Точность прогноза в точках проверки: средняя ошибка прогноза (MPE) и среднеквадратическая ошибка прогноза (RMSPE);

Применение регрессионного кригинга

Регрессионный кригинг используется в различных прикладных областях: от метеорологии, климатологии, почвенного картирования, геологического картирования, моделирования распределения видов и т. д. Единственное требование для использования регрессионного кригинга по сравнению, например, с обычным кригингом, заключается в том, что существует один или несколько слоев ковариат, которые в значительной степени коррелируют с интересующим признаком. Некоторые общие применения регрессионного кригинга:

Геостатистическое картографирование: Регрессионный кригинг позволяет использовать гибридные геостатистические методы для моделирования, например, пространственного распределения свойств почвы.
Уменьшение масштаба карт. Регрессионный кригинг можно использовать в качестве основы для уменьшения масштаба различных существующих карт с координатной сеткой. В этом случае слои ковариат должны быть доступны с лучшим разрешением (что соответствует интенсивности выборки), чем исходные точечные данные. ^[11]
Распространение ошибок : смоделированные карты, созданные с помощью модели регрессионного кригинга, можно использовать для тестирования сценариев и для оценки распространяемой неопределенности.

Алгоритмы, основанные на регрессионном кригинге, играют в геостатистике все более важную роль, поскольку число возможных ковариат увеличивается с каждым днем. ^[1] Например, DEM теперь доступны из ряда источников. Подробные и точные изображения топографии теперь можно заказать с помощью систем дистанционного зондирования, таких как SPOT и ASTER ; SPOT5 предлагает стереоскопический сканер высокого разрешения (HRS), который можно использовать для создания ЦМР с разрешением до 5 м. ^[12] Более мелкие перепады высот также можно получить с помощью бортовых лазерных сканеров. Стоимость данных либо бесплатна, либо снижается по мере развития технологий. НАСА записало большую часть топографии мира в ходе топографической миссии «Шаттл Радар» в 2000 году. ^[13] С лета 2004 года эти данные были доступны (например, через ftp Геологической службы США ) почти по всему земному шару с разрешением около 90 м (для североамериканского континента с разрешением около 30 м). Аналогичным образом, мультиспектральные изображения MODIS доступны для бесплатного скачивания с разрешением 250 м. Большой бесплатный репозиторий изображений Landsat также доступен для загрузки через Global Land Cover Facility (GLCF).

Ссылки

^ Jump up to: ^а ^б Пебесма, Эдзер Дж. (1 июля 2006 г.). «Роль внешних переменных и баз данных ГИС в геостатистическом анализе» (PDF) . Транзакции в ГИС . 10 (4): 615–632. дои : 10.1111/j.1467-9671.2006.01015.x . S2CID 22146107 .
^ Матерон, Жорж (1969). «Часть 1 Тетради Центра математической морфологии Фонтенбло». Универсальный кригинг . Национальная горная школа Парижа.
^ Кресси, Ноэль (2012). Статистика для пространственно-временных данных . Хобокен, Нью-Джерси: Уайли. ISBN 978-0-471-69274-4 .
^ Jump up to: ^а ^б Минасный, Будиман; МакБрэтни, Алекс Б. (31 июля 2007 г.). «Пространственное прогнозирование свойств почвы с использованием EBLUP с ковариационной функцией Матерна». Геодерма . 140 (4): 324–336. Бибкод : 2007Геоде.140..324М . doi : 10.1016/j.geoderma.2007.04.028 .
^ Jump up to: ^а ^б Кристенсен, Рональд (2001). Расширенное линейное моделирование: многомерные, временные ряды и пространственные данные; непараметрическая регрессия и максимизация поверхности отклика (2-е изд.). Нью-Йорк, штат Нью-Йорк [ua]: Springer. ISBN 978-0-387-95296-3 .
^ Гольдбергер, А.С. (1962). «Лучший линейный несмещенный прогноз в модели обобщенной линейной регрессии». Журнал Американской статистической ассоциации . 57 (298): 369–375. дои : 10.1080/01621459.1962.10480665 . JSTOR 2281645 .
^ Ахмед, Шакил; Де Марсили, Гислен (1 января 1987 г.). «Сравнение геостатистических методов оценки пропускаемости с использованием данных о пропускаемости и удельной мощности». Исследования водных ресурсов . 23 (9): 1717. Бибкод : 1987WRR....23.1717A . дои : 10.1029/WR023i009p01717 .
^ Оде, ИОА; МакБрэтни, AB; Читтлборо, ди-джей (31 июля 1995 г.). «Дальнейшие результаты по прогнозированию свойств почвы по признакам местности: гетеротопный кокригинг и регрессионный кригинг». Геодерма . 67 (3–4): 215–226. Бибкод : 1995Geode..67..215O . дои : 10.1016/0016-7061(95)00007-Б .
^ Jump up to: ^а ^б Хенгль, Томислав; Хёвелинк, Жерар Б.М.; Штейн, Альфред (30 апреля 2004 г.). «Общая основа для пространственного прогнозирования переменных почвы на основе регрессионного кригинга» (PDF) . Геодерма . 120 (1–2): 75–93. Бибкод : 2004Geode.120...75H . doi : 10.1016/j.geoderma.2003.08.018 .
^ Вебстер, Ричард; Оливер, Маргарет А. (2007). Геостатистика для ученых-экологов (2-е изд.). Чичестер: Уайли. ISBN 978-0-470-02858-2 .
^ Хенгль, Томислав; Баят, Бранислав; Благоевич, Драган; Рейтер, Ханнес И. (1 декабря 2008 г.). «Геостатистическое моделирование топографии с использованием вспомогательных карт» (PDF) . Компьютеры и геонауки . 34 (12): 1886–1899. Бибкод : 2008CG.....34.1886H . дои : 10.1016/j.cageo.2008.01.005 .
^ Тутен, Тьерри (30 апреля 2006 г.). «Генерация DSM на основе стереоданных HRG внутри трека SPOT-5 и стереоданных HRG поперек трека с использованием пространственной триангуляции и автокалибровки». Журнал фотограмметрии и дистанционного зондирования ISPRS . 60 (3): 170–181. Бибкод : 2006JPRS...60..170T . дои : 10.1016/j.isprsjprs.2006.02.003 .
^ Рабус, Бернхард; Эйнедер, Майкл; Рот, Ахим; Бамлер, Ричард (31 января 2003 г.). «Миссия по радиолокационной топографии шаттла - новый класс цифровых моделей рельефа, полученных с помощью космического радара». Журнал фотограмметрии и дистанционного зондирования ISPRS . 57 (4): 241–262. Бибкод : 2003JPRS...57..241R . дои : 10.1016/S0924-2716(02)00124-7 .

Дальнейшее чтение

Глава 2, Регрессия-кригинг , Томислав Хенгль (2009), Практическое руководство по геостатистическому картированию , 291 стр., ISBN 978-90-9024981-0 . [1]
Хенгль Т.; Хёвелинк ГБМ; Росситер Д.Г. (2007). «О регрессии-кригинге: от уравнений к практическим примерам». Компьютеры и геонауки . 33 (10): 1301–1315. Бибкод : 2007CG.....33.1301H . дои : 10.1016/j.cageo.2007.05.001 .

Внешние ссылки

Пакет Gstat (реализует KED)
Пакет GeoR (реализует KED)

[Pebesma2006IJGIS-1] Jump up to: ^а ^б Пебесма, Эдзер Дж. (1 июля 2006 г.). «Роль внешних переменных и баз данных ГИС в геостатистическом анализе» (PDF) . Транзакции в ГИС . 10 (4): 615–632. дои : 10.1111/j.1467-9671.2006.01015.x . S2CID 22146107 .

[2] Матерон, Жорж (1969). «Часть 1 Тетради Центра математической морфологии Фонтенбло». Универсальный кригинг . Национальная горная школа Парижа.

[Cressie2012Wiley-3] Кресси, Ноэль (2012). Статистика для пространственно-временных данных . Хобокен, Нью-Джерси: Уайли. ISBN 978-0-471-69274-4 .

[MinasnyMcBratney2007Geoderma-4] Jump up to: ^а ^б Минасный, Будиман; МакБрэтни, Алекс Б. (31 июля 2007 г.). «Пространственное прогнозирование свойств почвы с использованием EBLUP с ковариационной функцией Матерна». Геодерма . 140 (4): 324–336. Бибкод : 2007Геоде.140..324М . doi : 10.1016/j.geoderma.2007.04.028 .

[Christensen2001Springer-5] Jump up to: ^а ^б Кристенсен, Рональд (2001). Расширенное линейное моделирование: многомерные, временные ряды и пространственные данные; непараметрическая регрессия и максимизация поверхности отклика (2-е изд.). Нью-Йорк, штат Нью-Йорк [ua]: Springer. ISBN 978-0-387-95296-3 .

[Goldberger1962-6] Гольдбергер, А.С. (1962). «Лучший линейный несмещенный прогноз в модели обобщенной линейной регрессии». Журнал Американской статистической ассоциации . 57 (298): 369–375. дои : 10.1080/01621459.1962.10480665 . JSTOR 2281645 .

[7] Ахмед, Шакил; Де Марсили, Гислен (1 января 1987 г.). «Сравнение геостатистических методов оценки пропускаемости с использованием данных о пропускаемости и удельной мощности». Исследования водных ресурсов . 23 (9): 1717. Бибкод : 1987WRR....23.1717A . дои : 10.1029/WR023i009p01717 .

[Odeh1995-8] Оде, ИОА; МакБрэтни, AB; Читтлборо, ди-джей (31 июля 1995 г.). «Дальнейшие результаты по прогнозированию свойств почвы по признакам местности: гетеротопный кокригинг и регрессионный кригинг». Геодерма . 67 (3–4): 215–226. Бибкод : 1995Geode..67..215O . дои : 10.1016/0016-7061(95)00007-Б .

[Hengl2004Geoderma-9] Jump up to: ^а ^б Хенгль, Томислав; Хёвелинк, Жерар Б.М.; Штейн, Альфред (30 апреля 2004 г.). «Общая основа для пространственного прогнозирования переменных почвы на основе регрессионного кригинга» (PDF) . Геодерма . 120 (1–2): 75–93. Бибкод : 2004Geode.120...75H . doi : 10.1016/j.geoderma.2003.08.018 .

[WebsterOliver2007-10] Вебстер, Ричард; Оливер, Маргарет А. (2007). Геостатистика для ученых-экологов (2-е изд.). Чичестер: Уайли. ISBN 978-0-470-02858-2 .

[Hengl2008CG-11] Хенгль, Томислав; Баят, Бранислав; Благоевич, Драган; Рейтер, Ханнес И. (1 декабря 2008 г.). «Геостатистическое моделирование топографии с использованием вспомогательных карт» (PDF) . Компьютеры и геонауки . 34 (12): 1886–1899. Бибкод : 2008CG.....34.1886H . дои : 10.1016/j.cageo.2008.01.005 .

[12] Тутен, Тьерри (30 апреля 2006 г.). «Генерация DSM на основе стереоданных HRG внутри трека SPOT-5 и стереоданных HRG поперек трека с использованием пространственной триангуляции и автокалибровки». Журнал фотограмметрии и дистанционного зондирования ISPRS . 60 (3): 170–181. Бибкод : 2006JPRS...60..170T . дои : 10.1016/j.isprsjprs.2006.02.003 .

[13] Рабус, Бернхард; Эйнедер, Майкл; Рот, Ахим; Бамлер, Ричард (31 января 2003 г.). «Миссия по радиолокационной топографии шаттла - новый класс цифровых моделей рельефа, полученных с помощью космического радара». Журнал фотограмметрии и дистанционного зондирования ISPRS . 57 (4): 241–262. Бибкод : 2003JPRS...57..241R . дои : 10.1016/S0924-2716(02)00124-7 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]