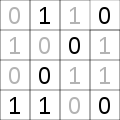
Такузу
Тема этой статьи Википедии может не соответствовать общему правилу по известности . ( июль 2015 г. ) |
Такузу , также известный как Бинаиро , представляет собой логическую головоломку, включающую размещение двух символов, часто 1 и 0, на прямоугольной сетке. Цель состоит в том, чтобы заполнить сетку единицами и нулями, где в каждой строке и столбце имеется одинаковое количество единиц и нулей и не более двух цифр любого числа, смежных друг с другом. Кроме того, не может быть одинаковых строк или столбцов. Как и в судоку , каждая головоломка начинается с уже заполненных нескольких квадратов сетки.
Имена и вариации
[ редактировать ]Игра известна как Бинаиро, Такузу, Бинеро, [1] [2] Тоху-ва-воху (Бесформенный и пустой), Эйнс и Цвай (Один и два), Бинарные головоломки, Бинохо, Зернеро, [3] Крестики-Так-Логика, [4] и двоичные судоку. [5] Названия «Бинаиро» и «Такузу» являются зарегистрированными товарными знаками Европейского Союза. [6] [7] Название «Binero» является зарегистрированной торговой маркой Editions Megastar во Франции. [8]
Определенные названия подразумевают использование определенных символов. Например, в двоичных головоломках используются 1 и 0 (т.е. двоичные числа ), в игре «Крестики-так-логика» используются X и O (например, крестики-нолики ), в Eins und Zwei используются 1 и 2, а в Tohu-Wa-Vohu используются буквы T и Символы В. Однако многие имена используются для любых вариаций символов. Черно-белые круги (или квадраты) — еще одна часто используемая пара символов. Любая вариация двух цифр, букв, цветов или изображений может работать как два символа, хотя обычно символы представляют собой 1, X или фигуры.
Размеры прямоугольной сетки могут сильно различаться. Поскольку цель состоит в том, чтобы иметь одинаковое количество символов в каждой строке и столбце, количество строк и столбцов обычно четное. Хотя это и не обязательно, сетки часто бывают квадратными. Общие размеры варьируются от 4x4 до 20x20. [9] [10] Также изготавливаются головоломки большего размера, в том числе с сеткой 30x40. [11]
Некоторые варианты допускают использование идентичных строк и столбцов. [3] Другой вариант, Odd Binairo, имеет нечетное количество строк и столбцов, каждый из которых содержит на единицу больше нуля, чем 0 (т.е. в сетке 11x11 каждая строка и столбец имеют 5 нулей и 6 единиц). [12]
История
[ редактировать ]У этой головоломки есть два конкурирующих источника, оба созданы примерно в одно и то же время. Тоху ва Воху придумал итальянец Адольфо Дзанеллати. [3] Binairo была создана бельгийцами Питером Де Шеппером и Фрэнком Куссементом в 2009 году. [1] [12]
Tic-Tac-Logic утверждает, что возникла из создания однопользовательской версии крестиков-ноликов. Как и в игре «крестики-нолики», здесь используются X и Os. Цель игры для двух игроков — собрать три подряд, а в игре «Тик-Так-Логика» цель — не допустить появления трех подряд. [4]
Методы решения
[ редактировать ]- Нерешенная сетка Такузу 4 × 4
- Та же сетка, решенная
- Каждая строка и каждый столбец должны содержать равное количество нулей и единиц. Следовательно, если в строке или столбце достигнуто необходимое количество нулей или единиц, оставшиеся ячейки должны содержать другую цифру (1xx101 → 100101).
- Более двух одинаковых цифр не могут находиться рядом. Следовательно, если две соседние ячейки содержат одну и ту же цифру, ячейки рядом с цифрами должны содержать другую цифру (xxx00x → xx1001). Аналогично, если две ячейки содержат одну и ту же цифру с одной пустой ячейкой между ними, эта пустая ячейка должна содержать другую цифру, потому что в противном случае появятся три одинаковые цифры (x1x1xx → x101xx).
- Устраните невозможное. Например, если шестая ячейка в 110xxx равна 1, балансировка количества нулей и единиц приводит к появлению тройки (110xxx → 110xx1 → 11 000 1), поэтому она не может быть 1. Следовательно, шестая ячейка должен содержать 0 (110xxx → 110xx0).
- Каждая строка и столбец уникальны (100101 и 1001xx → 100101 и 100110).
Математика
[ редактировать ]Доказательство с нулевым разглашением было опубликовано в июне 2016 года. головоломки [13] [14]
Головоломка была адаптирована для моделирования квантовых агентов. [15]
Математики голландского университета (П.Х. Утомо и Р.Х. Макарим) предложили три различных подхода к решению бинарных головоломок: использование поиска с обратным поиском, решателей SAT и алгоритмов на основе Грёбнера. [16] Последние два подхода сводят задачу решения бинарной головоломки к задаче булевой выполнимости и решению систем полиномиальных уравнений над бинарным полем.
Ссылки
[ редактировать ]- ^ Перейти обратно: а б Аберкейн, Идрисс Дж. (18 июля 2016 г.). «Комментарий: Бинаиро стимулирует нейроны!» [Как Бинаиро стимулирует нейроны!]. Ле Пуэнт (на французском языке) . Проверено 9 февраля 2019 г.
- ^ Кюссе, Майлис (23 июня 2016 г.). «Бинаиро, игра для любителей цифр» . Биба (на французском языке) . Проверено 9 февраля 2019 г.
- ^ Перейти обратно: а б с «Тоху-Ва-Воху» . janko.at (на немецком языке) . Проверено 9 февраля 2019 г.
- ^ Перейти обратно: а б «История Тик-Так-Логики» . Концептуальные головоломки . Проверено 9 февраля 2019 г.
- ^ «Двоичные судоку — Поиск в Google» . www.google.com .
- ^ «Информация о файле EUTM — Бинаиро» . ВИСПО . Проверено 9 февраля 2019 г.
- ^ «Информация о файле EUTM — Такузу» . ВИСПО . Проверено 9 февраля 2019 г.
- ^ "БИНЕРО РЕЛАКС (Маркес) - Данные ИНПИ" . data.inpi.fr.
- ^ «Бинаиро» . Бинаиро . Команда головоломок . Проверено 9 февраля 2019 г.
- ^ «Бинарная головоломка» . BinaryPuzzle.com . Проверено 9 февраля 2019 г.
- ^ «Специальный ежемесячный журнал Binairo» . Бинаиро . Команда головоломок . Проверено 9 февраля 2019 г.
- ^ Перейти обратно: а б «Четный и нечетный Бинаиро» . ПитерФранк . Проверено 9 февраля 2019 г.
- ^ Бултель, Ксавье; Драйер, Янник; Дюма, Жан-Вильям; Лафуркад, Паскаль (2016). «Физические доказательства нулевого знания для Акари, Такузу, Какуро и КенКена» arXiv : 1606.01045 [ cs.CR ].
- ^ Ксавье Бюльтель, Янник Драйер, Жан-Гийом Дюма и Паскаль Лафуркад4 «Физические доказательства нулевого разглашения для Акари, Такузу, Какуро и КенКена» (PDF )
{{cite web}}: CS1 maint: несколько имен: список авторов ( ссылка ) CS1 maint: числовые имена: список авторов ( ссылка ) - ^ Фужер, Ален-Жером (2017). «Агент, обладающий квантовыми свойствами: состояния суперпозиции и запутанность». Вычислительный коллективный разум . Конспекты лекций по информатике. Том. 10448. стр. 389–398. дои : 10.1007/978-3-319-67074-4_38 . ISBN 978-3-319-67073-7 .
- ^ Утомо, Путранто Х.; Макарим, Русиди Х. (2017). «Решение бинарной головоломки» . Математика в информатике . 11 (3–4): 515–526. дои : 10.1007/s11786-017-0322-4 .