Метод Халлада

Синус, косинус и версинус θ в единицах окружности с центром в точке O.

Метод Халлада , разработанный французом Эмилем Халладом, представляет собой метод, используемый в геометрии пути для съемки , проектирования и разметки кривых на железнодорожном пути. ^[1]

Он включает в себя измерение смещения струнной линии от внешней стороны кривой в центральной точке хорды . На самом деле струна слишком толстая, чтобы обеспечить четкое считывание показаний, и легко рвется при натяжении, необходимом для минимизации движения из-за ветра. Вместо этого можно использовать катушку с проволокой со специальными держателями (вилками Халлада), которые удерживают проволоку на фиксированном расстоянии от рельса. Измерение проводится с помощью правила Халлада, специальной линейки, нулевая точка которой соответствует смещению вилок, тем самым компенсируя его. Целью смещения является обеспечение возможности небольших отрицательных измерений. Без этого геодезистам часто приходилось бы читать с обеих сторон рельса, чтобы определить правильные значения на прямых участках пути, которые обычно имеют смесь небольших положительных и отрицательных значений.

Используется стандартная длина хорды: в Великобритании это обычно 30 метров, а иногда и 20 метров. Полухорды, т.е. интервалы 15 или 10 метров, отмечаются на базовой направляющей мелом. Затем струну длиной в один полный аккорд удерживают одним концом на двух метках на каждом конце аккорда и измеряют смещение на отметке половины аккорда.

Версину : хорды, равную этому измеренному значению смещения, можно рассчитать с использованием приближения

$\operatorname {versin} \theta =1-cos\,\theta$

что такое:

$v\approx {\frac {L^{2}}{8r}}$

где
$v$ = версия (м),
$L$ = длина хорды (м),
$r$ = радиус кривой (м)

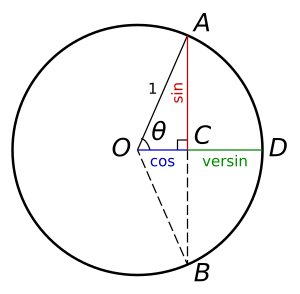
Эта формула верна и для других единиц измерения, например, для футов. Связь версины, хорды и радиуса выведена из теоремы Пифагора . Судя по схеме справа:

OC={\sqrt {OA^{2}-AC^{2}}}

Мы можем заменить OC на r (радиус) минус v, OA на r и AC на L/2 (половина хорды). Затем переформулируйте формулу так:

r-v={\sqrt {r^{2}-({\frac {L}{2}})^{2}}},

r^{2}-2rv+v^{2}=r^{2}-({\frac {L}{2}})^{2},

2r-v={\frac {L^{2}}{4v}},

r={\frac {L^{2}}{8v}}+{\frac {v}{2}}.

Поскольку изогнутые дорожки обычно большие, результат v/2 очень мал. Для упрощения формулы приведем приближение:

r\approx {\frac {L^{2}}{8v}}

Для нахождения версии заданной кривой постоянного радиуса можно использовать следующее: ^[2]

v\approx {\frac {L^{2}}{8r}}

Метод Халлада заключается в использовании аккорда для непрерывного измерения версуса в виде перекрывающегося рисунка вдоль кривой. Значения версуса для идеальной круговой кривой будут иметь одинаковый номер. ^[3] Сравнивая измеренные значения версин с расчетными версинами, это можно затем использовать для определения того, какие шпаклевки следует применить к пути, чтобы правильно выровнять кривую. Это часто делается с помощью колышков, которые вбиваются в землю в углублении рядом с направляющей, которую необходимо выровнять. Процесс установки колышков в правильное положение известен как «выставление».Если кривая должна иметь желаемый постоянный радиус, который обычно определяется физическими препятствиями и допустимой степенью наклона , версинусу можно рассчитать для желаемого радиуса, используя это приближение. На практике многие кривые пути представляют собой переходные кривые и поэтому имеют меняющийся радиус. Чтобы обеспечить плавный переход, различия в стихах между последовательными полуаккордами измеряются и минимизируются.

Исследование Халлада — это метод исследования, который использует тот же принцип для измерения версус вдоль существующей кривой. Основываясь на значениях версинусов, радиус этой круглой изогнутой дорожки можно приблизительно определить следующим образом: ^[4]

r\approx {\frac {L^{2}}{8v}}

Этот метод можно выполнить вручную, и этот метод до сих пор используется в Великобритании. Однако из-за сложности расчетов на больших длинах путей сейчас их часто выполняют с помощью компьютера. ^[5] при этом данные о геометрии пути загружаются прямо в машину для подбивки и облицовки с компьютерным управлением для реализации.

См. также

Ссылки

^ Ивницкий, Саймон (2006). Справочник по динамике железнодорожного транспорта . ЦРК Пресс. п. 448. ИСБН 0-8493-3321-0 .
^ Эллис, Иэн (1998). Учебное пособие Hallade (PDF) .
^ Эллис, составлено Иэном (2006). Британская энциклопедия железнодорожного машиностроения Эллиса: сборник специальных инженерных терминов, широко используемых на железных дорогах Великобритании . Роли, Северная Каролина: Лулу. п. 160. ИСБН 978-1-84728-643-7 . Проверено 22 ноября 2012 г.
^ : Кэмп, Уолтер Мейсон (1904). Примечания к ходу - Строительство и техническое обслуживание (второе издание, переработанное издание). Оберн-Парк, Чикаго: Лагерь Уолтера Мейсона. п. 232 . Проверено 22 ноября 2012 г.
^ «Железнодорожное программное обеспечение» . Проверено 7 июня 2010 г.

Внешние ссылки

Система Халлада
Халлад, Эмиль на Steamindex.com

[Iwnicki-1] Ивницкий, Саймон (2006). Справочник по динамике железнодорожного транспорта . ЦРК Пресс. п. 448. ИСБН 0-8493-3321-0 .

[2] Эллис, Иэн (1998). Учебное пособие Hallade (PDF) .

[3] Эллис, составлено Иэном (2006). Британская энциклопедия железнодорожного машиностроения Эллиса: сборник специальных инженерных терминов, широко используемых на железных дорогах Великобритании . Роли, Северная Каролина: Лулу. п. 160. ИСБН 978-1-84728-643-7 . Проверено 22 ноября 2012 г.

[4] : Кэмп, Уолтер Мейсон (1904). Примечания к ходу - Строительство и техническое обслуживание (второе издание, переработанное издание). Оберн-Парк, Чикаго: Лагерь Уолтера Мейсона. п. 232 . Проверено 22 ноября 2012 г.

[railsoft-5] «Железнодорожное программное обеспечение» . Проверено 7 июня 2010 г.

[1]

[2]

[3]

[4]

[5]