Правило 110

Клеточный автомат Правило 110 (часто называемый просто Правилом 110 ) представляет собой элементарный клеточный автомат с интересным поведением на границе между стабильностью и хаосом. В этом отношении она похожа на «Игру жизни» Конвея . Как и Жизнь, Правило 110 с определенным повторяющимся фоновым узором известно как полное по Тьюрингу . Это означает, что в принципе любой расчет или компьютерная программа могут быть смоделированы с использованием этого автомата.

Пример выполнения клеточного автомата правила 110 за 256 итераций, начиная с одной ячейки.

Определение

В элементарном клеточном автомате одномерный набор нулей и единиц развивается в соответствии с простым набором правил. Будет ли точка в шаблоне иметь значение 0 или 1 в новом поколении, зависит от ее текущего значения, а также от значений двух ее соседей.

Анимация того, как правила одномерного клеточного автомата определяют следующее поколение с использованием правила 110.

Автомат Правило 110 имеет следующий набор правил:

Текущий шаблон	111	110	101	100	011	010	001	000
Новое состояние центральной ячейки	0	1	1	0	1	1	1	0

Название «Правило 110» происходит от того факта, что это правило можно свести к двоичной последовательности 01101110; интерпретируемый как двоичное число , это соответствует десятичному значению 110. Это схема именования кода Wolfram .

История

В 2004 году Мэтью Кук опубликовал доказательство того, что правило 110 с определенным повторяющимся фоновым узором является полным по Тьюрингу , то есть способным к универсальным вычислениям , о чем Стивен Вольфрам предположил в 1985 году. Кук представил свое доказательство на конференции CA98 Института Санта-Фе перед публикацией книги Вольфрама «Новый вид науки» . Это привело к судебному делу, основанному на соглашении о неразглашении информации с Wolfram Research . Wolfram Research заблокировала публикацию доказательства Кука на несколько лет.

Интересные объекты

Среди 88 возможных уникальных элементарных клеточных автоматов правило 110 — единственное, для которого полнота по Тьюрингу была непосредственно доказана, хотя доказательства для нескольких подобных правил следуют как простые следствия (например, правило 124, которое является горизонтальным отражением правила 110). Правило 110, возможно, является простейшей известной полной системой Тьюринга.

Правило 110, как и Игра Жизни , демонстрирует то, что Вольфрам называет « поведением класса 4 », которое не является ни полностью стабильным, ни полностью хаотичным. Локализованные структуры появляются и взаимодействуют сложным образом.

Мэтью Кук доказал, что Правило 110 способно поддерживать универсальные вычисления путем последовательной эмуляции циклических систем тегов , затем системы с двумя тегами , а затем машин Тьюринга . Заключительный этап требует экспоненциальных затрат времени, поскольку лента машины Тьюринга закодирована в унарной системе счисления . Нири и Вудс (2006) представили другую конструкцию, которая заменяет двухтеговые системы машинами Тьюринга по часовой стрелке и имеет полиномиальные накладные расходы.

Доказательство универсальности

Мэтью Кук представил свое доказательство универсальности Правила 110 на конференции Института Санта-Фе, состоявшейся перед публикацией « Нового вида науки» . Компания Wolfram Research заявила, что эта презентация нарушает соглашение Кука о неразглашении информации с его работодателем, и добилась постановления суда об исключении статьи Кука из опубликованных материалов конференции. Тем не менее о существовании доказательства Кука стало известно. Интерес к его доказательству был вызван не столько его результатом, сколько его методами, в частности техническими деталями его построения. Характер доказательства Кука значительно отличается от обсуждения правила 110 в книге «Новый вид науки» . С тех пор Кук написал статью, в которой изложил свое полное доказательство.

Кук доказал, что Правило 110 было универсальным (или полным по Тьюрингу), показав, что можно использовать это правило для эмуляции другой вычислительной модели — системы циклических тегов , которая, как известно, универсальна. Он первым выделил несколько космических кораблей , самовоспроизводящихся локализованных моделей, которые можно было построить по бесконечно повторяющемуся шаблону во вселенной Правила 110. Затем он разработал способ взаимодействия комбинаций этих структур таким образом, чтобы его можно было использовать для вычислений.

Космические корабли в Правиле 110

Функция универсальной машины в Правиле 110 требует, чтобы конечное число локализованных шаблонов было встроено в бесконечно повторяющийся фоновый шаблон. Фоновый узор имеет ширину четырнадцать ячеек и повторяется ровно каждые семь итераций. Шаблон: 00010011011111 .

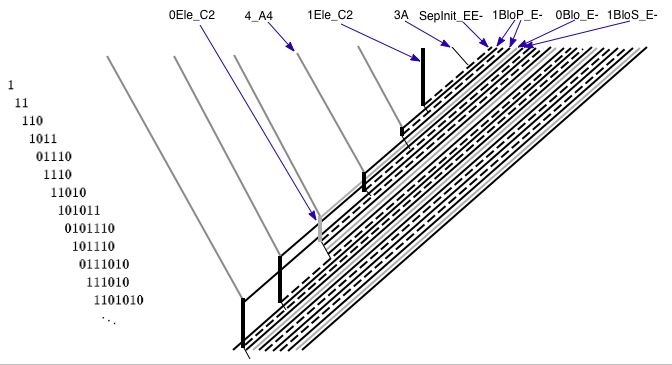
Три локализованных шаблона имеют особое значение в универсальной машине по Правилу 110. Они показаны на изображении ниже и окружены повторяющимся фоновым узором. Крайняя левая структура смещается на две клетки вправо и повторяется каждые три поколения. Он включает в себя последовательность 0001110111, окруженную фоновым узором, приведенным выше, а также две разные эволюции этой последовательности.

На рисунках время течет сверху вниз: верхняя линия представляет исходное состояние, а каждая следующая линия — состояние в следующий момент времени.

Центральная структура смещается на восемь клеток влево и повторяется каждые тридцать поколений. Он включает в себя последовательность 1001111, окруженную фоновым узором, приведенным выше, а также двадцать девять различных вариантов развития этой последовательности.

Самая правая структура остается стационарной и повторяется каждые семь поколений. Он включает в себя последовательность 111, окруженную фоновым узором, приведенным выше, а также пять различных вариантов развития этой последовательности.

Ниже показано изображение, показывающее, как первые две структуры проходят друг через друга, не взаимодействуя, кроме как посредством трансляции (слева), и взаимодействуя, образуя третью структуру (справа).

В Правиле 110 есть множество других космических кораблей, но они не занимают столь заметного места в доказательстве универсальности.

Построение циклической системы тегов

Механизм системы циклических тегов состоит из трех основных компонентов:

• Строка данных , которая является стационарной;
• Бесконечно повторяющаяся серия конечных производственных правил , которые начинаются справа и движутся влево;
• Бесконечно повторяющаяся серия тактовых импульсов , которые начинаются слева и движутся вправо.

Исходное расстояние между этими компонентами имеет первостепенное значение. Чтобы клеточный автомат реализовал систему циклических тегов, начальные условия автомата должны быть тщательно выбраны так, чтобы различные локализованные структуры, содержащиеся в них, взаимодействовали высокоупорядоченным образом.

Строка данных в системе циклических тегов представлена ​​серией стационарных повторяющихся структур показанного выше типа. Различное количество горизонтального пространства между этими структурами позволяет отличить 1 символ от 0 символов. Эти символы представляют собой слово , с которым работает система циклических тегов, и первый такой символ уничтожается при рассмотрении каждого правила производства. Если этот ведущий символ равен 1, в конец строки добавляются новые символы; когда он равен 0, новые символы не добавляются. Механизм достижения этого описан ниже.

Справа входят ряд движущихся влево структур, показанных выше, разделенных разным количеством горизонтального пространства. Большое количество этих структур комбинируется с разными интервалами для обозначения 0 и 1 в правилах производства системы циклических тегов. Поскольку правила производства системы тегов известны во время создания программы и бесконечно повторяются, шаблоны 0 и 1 в начальном состоянии могут быть представлены бесконечно повторяющейся строкой. Каждое производственное правило отделено от следующего другой структурой, известной как разделитель правил (или разделитель блоков ), которая перемещается влево с той же скоростью, что и кодирование продуктивных правил.

Когда разделитель правил с перемещением влево встречает стационарный символ в строке данных системы циклических тегов, это приводит к уничтожению первого встреченного символа. Однако его последующее поведение варьируется в зависимости от того, был ли символ, закодированный строкой, 0 или 1. Если 0, разделитель правил меняется на новую структуру, которая блокирует входящее производственное правило. Эта новая структура уничтожается, когда она встречает следующий разделитель правил.

Если, с другой стороны, символом в строке была 1, разделитель правил изменится на новую структуру, которая допускает входящее производственное правило. Хотя новая структура снова уничтожается при встрече со следующим разделителем правил, она сначала позволяет ряду структур пройти влево. Затем эти структуры добавляются в конец строки данных системы циклических тегов. Это окончательное преобразование осуществляется с помощью серии бесконечно повторяющихся, движущихся вправо тактовых импульсов по схеме, движущейся вправо, показанной выше. Тактовые импульсы преобразуют входящие 1-символы, движущиеся влево, из производственного правила в стационарные 1-символы строки данных, а входящие 0-символы из производственного правила в стационарные 0-символы строки данных.

Циклическая система тегов работает

На рисунке выше показана схема реконструкции циклической системы тегов в Правиле 110.

См. также

• Правило 30
• Правило 90
• Правило 184

Ссылки

Цитируемые работы

• Кук, Мэтью (2004). «Универсальность в элементарных клеточных автоматах» (PDF) . Сложные системы . 15 :1–40.
• Джайлз, Джим (2002). «Что это за наука?» . Природа . 417 (6886): 216–218. Бибкод : 2002Natur.417..216G . дои : 10.1038/417216a . ПМИД   12015565 . S2CID   10636328 .
• Нири, Терлоу; Вудс, Дэмиен (2006). «П-полнота клеточного автомата Правило 110». В Бульези, Микеле; Пренил, Барт; Сассоне, Владимиро; Вегенер, Инго (ред.). Автоматы, языки и программирование: 33-й международный коллоквиум, ICALP 2006, Венеция, Италия, 10–14 июля 2006 г., Материалы, часть I. Конспекты лекций по информатике. Том. 4051. Спрингер. стр. 132–143. дои : 10.1007/11786986_13 .
• Вольфрам, Стивен (2002). Новый вид науки . Вольфрам Медиа. ISBN  1-57955-008-8 .

Дальнейшее чтение

• Кук, Мэтью (2008). «Конкретный взгляд на вычисления по правилу 110». В Нири, Т.; Вудс, Д.; Седа, АК; Мерфи, Н. (ред.). Сложность простых программ . Электронные труды по теоретической информатике. Том. 1. С. 31–55. arXiv : 0906.3248v1 . дои : 10.4204/EPTCS.1.4 . S2CID   10266058 .
• Мартинес, Хенаро Х.; Адамацкий А.; Чен, Фангюэ; Чуа, Леон (2012). «О солитонных столкновениях между локализациями в сложных элементарных клеточных автоматах: правила 54, 110 и далее». Сложные системы . 21 (2): 117–142. arXiv : 1301.6258 . дои : 10.25088/ComplexSystems.21.2.117 . S2CID   10165042 .
• Мартинес, Хенаро Х.; Адамацкий А.; Стивенс, Кристофер Р.; Хёфлих, Алехандро Ф. (2011). «Клеточно-автоматные суперколлайдеры» . Межд. Дж. Мод. Физ. С. ​ 22 (4): 419–439. arXiv : 1105.4332 . Бибкод : 2011IJMPC..22..419M . дои : 10.1142/S0129183111016348 . S2CID   7508070 .
• Мартинес, Хенаро Х.; Макинтош, Гарольд В .; Мора, Хуан КСТ; Вергара, Серджио ВК (2003–2008). «Воспроизведение систем циклических тегов, разработанных Мэтью Куком, с использованием правила 110 с использованием фаз fi_1» (PDF) . Журнал клеточных автоматов . 6 (2–3): 121–161.
• Мартинес, Хенаро Х.; Макинтош, Гарольд В .; Мора, Хуан КСТ; Вергара, Серджио ВК (2008). «Определение регулярного языка с помощью структур на основе планера, называемых фазами fi_1 в Правиле 110». Журнал клеточных автоматов . 3 (3): 231–270. arXiv : 0706.3348v1 . Бибкод : 2007arXiv0706.3348J .
• Мартинес, Хенаро Х.; Макинтош, Гарольд В .; Мора, Хуан КСТ; Вергара, Серджио ВК (2007). «Правило 110, основанное на столкновениях объектов и других конструкций» (PDF) . Журнал клеточных автоматов . 2 (3): 219–242.
• Мартинес, Хенаро Х.; Макинтош, Гарольд В .; Мора, Хуан КСТ (2006). «Планеры в Правиле 110» (PDF) . Межд. Дж. Нетрадиционных вычислений . 2 :1–49.
• Мартинес, Хенаро Х.; Макинтош, Гарольд В .; Мора, Хуан КСТ (2003). «Производство планеров путем столкновений в Правиле 110» (PDF) . Достижения в области искусственной жизни . Конспекты лекций по информатике. Том. 2801. стр. 175–182. дои : 10.1007/978-3-540-39432-7_19 . ISBN  978-3-540-20057-4 .
• Мартинес, Хенаро Х.; Макинтош, Гарольд В. (2001). «АТЛАС: Столкновения планеров как фазы эфира в правиле 110» .
• Макинтош, Гарольд В. (1999). «Правило 110 в отношении наличия планеров» (PDF) .
• Макинтош, Гарольд В. (2002). «Правило 110 универсально!» (PDF) .

Внешние ссылки

• Правило 110 — из Wolfram MathWorld
• Правило 110 в атласе клеточных автоматов Вольфрама.
• Репозиторий правила 110
• Механическая реализация 4-битного компьютера по Правилу 110 на основе мрамора.