Многосортная логика

Многосортная логика может формально отражать наше намерение не рассматривать вселенную как однородную коллекцию объектов, а разделить ее способом, аналогичным типам в типизированном программировании . И функциональные, и утвердительные « части речи » на языке логики отражают это типовое разделение вселенной даже на уровне синтаксиса: замена и передача аргументов могут выполняться только соответствующим образом, соблюдая «сортировки».

Существуют различные способы формализовать упомянутое выше намерение; многосортная логика — это любой пакет информации, который ее выполняет. В большинстве случаев указываются:

какой-то набор, S
соответствующее обобщение понятия подписи , позволяющее обрабатывать дополнительную информацию, поступающую с сортировками.

Область дискурса любой структуры этой сигнатуры затем фрагментируется на непересекающиеся подмножества, по одному для каждого вида.

Пример

Рассуждая о биологических организмах, полезно различать два вида: $\mathrm {plant}$ и $\mathrm {animal}$ . В то время как функция $\mathrm {mother} \colon \mathrm {animal} \to \mathrm {animal}$ имеет смысл, аналогичная функция $\mathrm {mother} \colon \mathrm {plant} \to \mathrm {plant}$ обычно нет. Многосортная логика позволяет использовать такие термины, как $\mathrm {mother} (\mathrm {lassie} )$ , но отбросить такие термины, как $\mathrm {mother} (\mathrm {my\_favorite\_oak} )$ как синтаксически неправильно оформленное.

Алгебраизация

Алгебраизация многосортной логики объясняется в статье Калейру и Гонсалвеша: ^[1] который обобщает абстрактную алгебраическую логику на многосортный случай, но также может использоваться в качестве вводного материала.

Логика сортировки по порядку

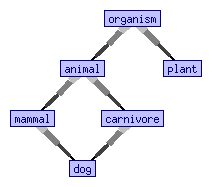
В то время как логика множественной сортировки требует, чтобы два различных сорта имели непересекающиеся наборы юниверсов, упорядоченной сортировки допускает один сорт. логика $s_{1}$ быть объявленным подвидом другого вида $s_{2}$ , обычно путем написания $s_{1}\subseteq s_{2}$ или аналогичный синтаксис. В приведенном выше примере биологии желательно объявить

{\text{dog}}\subseteq {\text{carnivore}}

,

{\text{dog}}\subseteq {\text{mammal}}

,

{\text{carnivore}}\subseteq {\text{animal}}

,

{\text{mammal}}\subseteq {\text{animal}}

,

{\text{animal}}\subseteq {\text{organism}}

,

{\text{plant}}\subseteq {\text{organism}}

,

и так далее; ср. картина.

Везде, где термин какой-то $s$ является обязательным, термин любого подвида $s$ вместо этого можно поставить ( принцип замены Лискова ). Например, если предположить, что объявление функции ${\text{mother}}:{\text{animal}}\longrightarrow {\text{animal}}$ и постоянное объявление ${\text{lassie}}:{\text{dog}}$ , термин ${\text{mother}}({\text{lassie}})$ совершенно действителен и имеет вид ${\text{animal}}$ . Чтобы предоставить информацию о том, что мать собаки, в свою очередь, является собакой, еще одно заявление ${\text{mother}}:{\text{dog}}\longrightarrow {\text{dog}}$ может быть выдан; это называется перегрузкой функций , аналогично перегрузке в языках программирования .

Логику с упорядоченной сортировкой можно преобразовать в несортированную с помощью унарного предиката. $p_{i}(x)$ для каждого сорта $s_{i}$ и аксиома $\forall x(p_{i}(x)\rightarrow p_{j}(x))$ для каждой декларации подсорта $s_{i}\subseteq s_{j}$ . Обратный подход оказался успешным в автоматизированном доказательстве теорем: в 1985 году Кристоф Вальтер смог решить тогдашнюю эталонную задачу, переведя ее в логику упорядоченной сортировки, тем самым уменьшив ее на порядок, поскольку многие унарные предикаты превратились в сортировки. ^[2]

Чтобы включить логику сортировки по порядку в автоматизированное средство доказательства теорем на основе предложений, объединения с сортировкой по порядку , который требует, чтобы любые два объявленных вида необходим соответствующий алгоритм $s_{1},s_{2}$ их пересечение $s_{1}\cap s_{2}$ тоже должно быть объявлено: если $x_{1}$ и $x_{2}$ являются переменными типа $s_{1}$ и $s_{2}$ , соответственно, уравнение $x_{1}{\stackrel {?}{=}}\,x_{2}$ есть решение $\{x_{1}=x,\;x_{2}=x\}$ , где $x:s_{1}\cap s_{2}$ .

Смолка обобщил логику упорядоченной сортировки, допускающую параметрический полиморфизм . ^[3]^[4]В его рамках объявления подсортировки передаются в выражения сложного типа.В качестве примера программирования, параметрическая сортировка ${\text{list}}(X)$ может быть объявлено (с $X$ являющийся параметром типа, как в шаблоне C++ ), и из объявления подсортировки ${\text{int}}\subseteq {\text{float}}$ отношение ${\text{list}}({\text{int}})\subseteq {\text{list}}({\text{float}})$ автоматически выводится, что означает, что каждый список целых чисел также является списком чисел с плавающей запятой.

Шмидт-Шаус обобщил логику упорядоченной сортировки, позволяющую объявлять термины. ^[5]В качестве примера, предполагая объявления подсортировки ${\text{even}}\subseteq {\text{int}}$ и ${\text{odd}}\subseteq {\text{int}}$ , объявление термина, например $\forall i:{\text{int}}.\;(i+i):{\text{even}}$ позволяет объявить свойство сложения целых чисел, которое невозможно выразить обычной перегрузкой.

См. также

Ссылки

^ Карлос Калейро, Рикардо Гонсалвес (2006). «Об алгебраизации многосортных логик». Учеб. 18-й межд. конф. о последних тенденциях в методах алгебраической разработки (WADT) (PDF) . Спрингер. стр. 21–36. ISBN 978-3-540-71997-7 .
^ Вальтер, Кристоф (1985). «Механическое решение парового катка Шуберта с помощью многосортного разрешения» (PDF) . Артиф. Интелл . 26 (2): 217–224. дои : 10.1016/0004-3702(85)90029-3 .
^ Смолка, Герт (ноябрь 1988 г.). «Логическое программирование с полиморфно отсортированными типами». Межд. Практикум по алгебраическому и логическому программированию . ЛНКС. Том. 343. Спрингер. стр. 53–70.
^ Смолка, Герт (май 1989 г.), Логическое программирование для типов с полиморфной упорядоченной сортировкой (докторская диссертация), Университет Кайзерслаутерн-Ландау , Германия
^ Шмидт-Шаус, Манфред (апрель 1988 г.). Вычислительные аспекты логики упорядоченной сортировки с объявлениями термов . ЛНАИ. Том. 395. Спрингер.

Ранние статьи по многосортной логике включают:

Ван, Хао (1952). «Логика многообразных теорий». Журнал символической логики . 17 (2): 105–116. дои : 10.2307/2266241 . JSTOR 2266241 . , собранные в книге автора «Вычисления, логика, философия». Сборник очерков , Пекин: Science Press; Дордрехт: Kluwer Academic, 1990.
Гилмор, ПК (1958). «Дополнение к «Логике многообразных теорий» » (PDF) . Математическая композиция . 13 : 277–281.
А. Обершельп (1962). «Исследования кванторной логики мультисортировки» . Математические летописи . 145 (4): 297–333. дои : 10.1007/bf01396685 . S2CID 123363080 . Архивировано из оригинала 20 февраля 2015 г. Проверено 11 сентября 2013 г.
Ф. Джеффри Пеллетье (1972). «Сортальная количественная оценка и ограниченная количественная оценка» (PDF) . Философские исследования . 23 (6): 400–404. дои : 10.1007/bf00355532 . S2CID 170303654 .

Внешние ссылки

«Множественная логика», первая глава в конспектах лекций по процедурам принятия решений Калоджеро Дж. Зарбы.

[1] Карлос Калейро, Рикардо Гонсалвес (2006). «Об алгебраизации многосортных логик». Учеб. 18-й межд. конф. о последних тенденциях в методах алгебраической разработки (WADT) (PDF) . Спрингер. стр. 21–36. ISBN 978-3-540-71997-7 .

[2] Вальтер, Кристоф (1985). «Механическое решение парового катка Шуберта с помощью многосортного разрешения» (PDF) . Артиф. Интелл . 26 (2): 217–224. дои : 10.1016/0004-3702(85)90029-3 .

[3] Смолка, Герт (ноябрь 1988 г.). «Логическое программирование с полиморфно отсортированными типами». Межд. Практикум по алгебраическому и логическому программированию . ЛНКС. Том. 343. Спрингер. стр. 53–70.

[4] Смолка, Герт (май 1989 г.), Логическое программирование для типов с полиморфной упорядоченной сортировкой (докторская диссертация), Университет Кайзерслаутерн-Ландау , Германия

[5] Шмидт-Шаус, Манфред (апрель 1988 г.). Вычислительные аспекты логики упорядоченной сортировки с объявлениями термов . ЛНАИ. Том. 395. Спрингер.

[1]

[2]

[3]

[4]

[5]