Схема паука

В математике унитарная диаграмма паука добавляет экзистенциальные точки к диаграмме Эйлера или Венна . Точки указывают на существование признака, описываемого пересечением контуров на диаграмме Эйлера. Эти точки можно соединить, образуя форму паука . Соединение точек представляет собой условие «или», также известное как логическая дизъюнкция .

Диаграмма паука — это логическое выражение, включающее унитарные диаграммы паука и логические символы. $\land ,\lor ,\lnot$ . Например, он может состоять из соединения двух диаграмм-пауков, дизъюнкции двух диаграмм-пауков или отрицания диаграммы-паука.

Пример

Логическая дизъюнкция, наложенная на диаграмму Эйлера

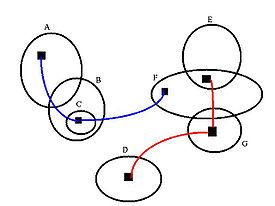
На показанном изображении из диаграммы Эйлера очевидны следующие соединения.

A\land B

B\land C

F\land E

G\land F

Во вселенной дискурса, определяемой этой диаграммой Эйлера , в дополнение к указанным выше союзам все множества от A до G , за исключением C , доступны отдельно. Набор C как подмножество B. доступен только Часто в сложных диаграммах одиночные множества и/или соединения могут быть скрыты другими комбинациями множеств.

Два паука в примере соответствуют следующим логическим выражениям:

Красный паук: $(F\land E)\lor (G)\lor (D)$
Синий паук: $(A)\lor (C\land B)\lor (F)$

Ссылки

Хауз Дж., Стэплтон Г. и Тейлор Х. Диаграммы Паука Лондонского математического общества , (2005) т. 8, стр. 145–194. Журнал вычислений и математики ISSN 1461-1570. По состоянию на 8 января 2012 г. здесь.
Стэплтон Г., Хауз Дж., Тейлор Дж. и Томпсон С. Что могут сказать паутинные диаграммы? Учеб. Диаграммы, (2004), т. 168, стр. 169–219. Доступ осуществлен 4 января 2012 г. здесь.
Стэплтон Г., Джамник М. и Мастхофф Дж. О читабельности диаграммных доказательств, Proc. Семинар по автоматизированному рассуждению, 2009. PDF.

Внешние ссылки

Университет Брайтона и Кента - Диаграммы Эйлера