Калейдоцикл

Правильные пирамиды с регулярным основанием
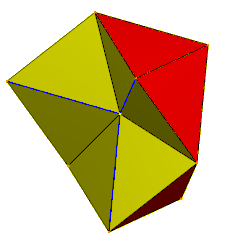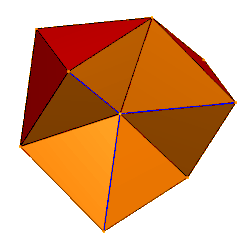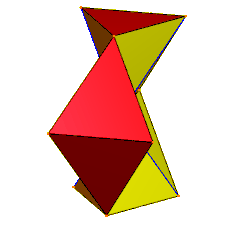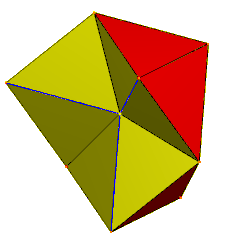Шесть тетраэдров, вершины которых встречаются в центре. Синие края удваиваются, пары граней скрыты.
Лица	24 равнобедренных треугольника
Края	36 (6 как вырожденные пары)
Вершины	12
Группа симметрии	C _{3 v} , [3], (*33), порядок 6
Характеристики	тор
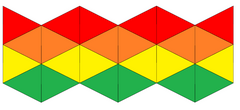Сеть

Калейдоцикл соединяющий или флекстангл — это гибкий многогранник, шесть тетраэдров (или дисфеноидов ) на противоположных рёбрах в цикл. Если грани дисфеноидов представляют собой равносторонние треугольники, их можно построить из натянутой треугольной сети замощений с четырьмя треугольниками в одном направлении и четным числом в другом направлении.

Калейдоцикл имеет вырожденные пары совпадающих при переходе ребер, которые действуют как шарниры. Калейдоцикл обладает дополнительным свойством: его можно непрерывно вращать вокруг оси кольца, показывая 4 набора по 6 треугольных граней. Калейдоцикл инвариантен относительно поворотов вокруг оси кольца на $k\pi /2$ , где $k$ является целым числом и, следовательно, может непрерывно скручиваться.

Калейдоциклы можно построить из одного листа бумаги (размерами $l\times 2l$ ) без разрывов и использования клея. Из-за этого, а также из-за их способности непрерывного скручивания их часто приводят в качестве примеров простых игрушек -оригами . Калейдоцикл иногда называют флексаэдром по аналогии с плоским флексагоном , который имеет аналогичную симметрию при изгибающих преобразованиях.

Примеры

Эта анимация демонстрирует изгиб калейдоцикла вокруг оси кольца. Четыре набора из 6 треугольных граней показаны разными цветами (все остальные грани в каждом наборе из шести показаны серым для контраста).

Вариации

Помимо шести сторон, можно соединить в цепочку большее четное количество тетраэдров: 8, 10, 12 и т. Д. Эти модели оставят центральный зазор в зависимости от пропорций граней треугольника. ^[1]

История

Уоллес Уокер придумал слово «калейдоцикл» в 1950-х годах от греческого «калос» (красивый), «эйдос» (форма) и «киклос» (кольцо).

В 1977 году Дорис Шатшнайдер и Уоллес Уокер опубликовали книгу о них, используя шаблоны MC Escher . ^[2]^[3]

Культурное использование

назвали эту форму гибким клубком Персонажи научно-фантастического приключенческого фильма 2018 года « Морщина во времени» , в котором была изображена бумажная модель с внутренними гранями, раскрашенными сердечками и узорами, которые становятся скрытыми, когда эти грани складываются вместе. Бумажная игрушка подсказала, как можно сложить пространство и время, чтобы объяснить волшебные путешествия из этой истории. Игрушку подарил дочери ее отец в начале фильма, и ее сердечки показывают, как любовь может быть окутана и оставаться там, даже после того, как отец загадочным образом исчезает. ^[4]

См. также

Ссылки

^ решения правильных тетраэдров, 8, 10, 12 с помощью Mathematica
↑ Рецензия на книгу: Искусство встречает математику в «Калейдоциклах» , 27 мая 1988 г.
^ Дорис Шатшнайдер и Уокер, MC Escher Kaleidocycles , 1977. ISBN 0-906212-28-6 . [1]
^ Купер, Меган (8 марта 2018 г.). «Диснеевский фильм «Трещина во времени»: калейдоцикл Flextangle и печатные формы для занятий» . Джамонки . Проверено 15 октября 2018 г.

Внешние ссылки

Эта многогранникам, статья, посвященная незавершена . Вы можете помочь Википедии, расширив ее .

[1] решения правильных тетраэдров, 8, 10, 12 с помощью Mathematica

[2] Рецензия на книгу: Искусство встречает математику в «Калейдоциклах» , 27 мая 1988 г.

[3] Дорис Шатшнайдер и Уокер, MC Escher Kaleidocycles , 1977. ISBN 0-906212-28-6 . [1]

[4] Купер, Меган (8 марта 2018 г.). «Диснеевский фильм «Трещина во времени»: калейдоцикл Flextangle и печатные формы для занятий» . Джамонки . Проверено 15 октября 2018 г.

[1]

[2]

[3]

[4]