Угловое разрешение (график)

Этот рисунок графа гиперкуба имеет угловое разрешение π/4 .

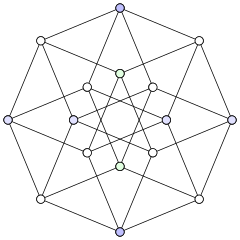
При рисовании графов угловое разрешение рисунка графа — это самый острый угол, образованный любыми двумя ребрами, которые встречаются в общей вершине рисунка.

Характеристики

Связь со степенью вершины

Форман и др. (1993) заметили, что каждый прямолинейный рисунок графа с максимальной степенью d имеет угловое разрешение не более 2π/ d : если v — вершина степени d , то ребра, инцидентные v, делят пространство вокруг v на d клиньев с общий угол 2π , а наименьший из этих клиньев должен иметь угол не более 2π/ d . Более строго: если граф является d - регулярным , он должен иметь угловое разрешение меньше, чем ${\frac {\pi }{d-1}}$, поскольку это наилучшее разрешение, которого можно достичь для вершины выпуклой оболочки рисунка.

Связь с раскраской графа

Как отметил Форман и др. (1993) максимально возможное угловое разрешение графа G тесно связано с хроматическим числом квадрата показали, что G. ² , граф на одном и том же множестве вершин, в котором пары вершин соединены ребром, если их расстояние в G не превышает двух. Если Г ² можно раскрасить в цвета χ , то G можно нарисовать с угловым разрешением π/ χ − ε для любого ε > 0 , назначив разные цвета вершинам правильного χ -угольника и поместив каждую вершину G близко к многоугольнику. вершина одного цвета. Используя эту конструкцию, они показали, что каждый граф максимальной степени d имеет рисунок с угловым разрешением, пропорциональным 1/ d. ² . Эта оценка близка к точной: они использовали вероятностный метод , чтобы доказать существование графов с максимальной степенью d , все рисунки которых имеют угловое разрешение. $O\left({\frac {\log d}{d^{2}}}\right)$.

Наличие оптимальных чертежей

Форман и др. (1993) привели пример, показывающий, что существуют графики, на которых нет рисунка, обеспечивающего максимально возможное угловое разрешение; вместо этого эти графики имеют семейство рисунков, угловое разрешение которых стремится к некоторому предельному значению, но не достигает его. В частности, они продемонстрировали граф с 11 вершинами, который имеет чертежи с угловым разрешением π/3 − ε для любого ε > 0 , но не имеет чертежа с угловым разрешением ровно π/3 .

Специальные классы графов

Деревья

Каждое дерево можно нарисовать таким образом, чтобы края были равномерно распределены вокруг каждой вершины — свойство, известное как идеальное угловое разрешение . Более того, если ребра могут свободно переставляться вокруг каждой вершины, то такое рисование возможно без пересечений, со всеми ребрами единичной или большей длины и с укладкой всего рисунка в ограничивающую рамку полиномиальной площади . Однако если циклический порядок ребер вокруг каждой вершины уже определен как часть входных данных задачи, то для достижения идеального углового разрешения без пересечений иногда может потребоваться экспоненциальная область.

Внепланарные графы

Идеальное угловое разрешение не всегда возможно для внешнепланарных графов , поскольку вершины выпуклой оболочки чертежа со степенью больше единицы не могут располагать инцидентные ребра на равном расстоянии друг от друга. Тем не менее, каждый внешнепланарный граф максимальной степени d имеет внешнепланарный рисунок с угловым разрешением, пропорциональным 1/ d .

Планарные графы

Для плоских графов с максимальной степенью d используется метод раскраски квадратов Формана и др. (1993) представил рисунок с угловым разрешением, пропорциональным 1/ d , поскольку квадрат плоского графа должен иметь хроматическое число, пропорциональное d . Точнее, в 1977 году Вегнер предположил, что хроматическое число квадрата плоского графа не превосходит $\max \left(d+5,{\frac {3d}{2}}+1\right)$, и известно, что хроматическое число не более ${\frac {5d}{3}}+O(1)$. Однако рисунки, полученные с помощью этой техники, обычно не плоские.

Для некоторых плоских графов оптимальное угловое разрешение плоского прямолинейного рисунка составляет O(1/ d ³ ) , где d — степень графа. Кроме того, в таком чертеже могут быть вынуждены использовать очень длинные ребра, экспоненциально длиннее самых коротких ребер на чертеже. Малиц и Папакостас (1994) использовали теорему об упаковке кругов и лемму о кольцах , чтобы показать, что каждый планарный граф с максимальной степенью d имеет планарный рисунок, угловое разрешение которого в худшем случае является экспоненциальной функцией от d , независимо от количества вершин в графе.

Вычислительная сложность

NP-трудно определить, имеет ли данный граф максимальной степени d рисунок с угловым разрешением 2π/ d , даже в частном случае, когда d = 4 . Однако для некоторых ограниченных классов рисунков, включая рисунки деревьев, в которых расширение листьев до бесконечности приводит к выпуклому подразделению плоскости, а также рисунки плоских графов, в которых каждая ограниченная грань представляет собой центрально-симметричный многоугольник, рисунок оптимального Угловое разрешение может быть найдено за полиномиальное время .

История

Угловое разрешение было впервые определено Форманом и др. (1993) .

Хотя первоначально это определение было определено только для прямолинейных рисунков графов, более поздние авторы также исследовали угловое разрешение рисунков, ребра которых представляют собой многоугольные цепочки. круговые дуги, или сплайновые кривые.

Угловое разрешение графика тесно связано с разрешением его пересечений, углом, образованным пересечениями на рисунке графика. В частности, чертеж RAC направлен на то, чтобы все эти углы были прямыми , то есть максимально возможным углом пересечения.

Ссылки

• Брандес, Ульрик ; Шубина, Галина; Тамассиа, Роберто (2000), «Улучшение углового разрешения при визуализации географических сетей», Data Visualization 2000: Proceedings of the Joint Eurographics и IEEE TCVG Symposium on Visualization в Амстердаме, Нидерланды, 29-31 мая 2000 г. , doi : 10.1007/ 978-3-7091-6783-0_3 , ISBN  9783211835159 .
• Карлсон, Джозайя; Эппштейн, Дэвид (2007), «Деревья с выпуклыми гранями и оптимальными углами», Кауфманн, Майкл; Вагнер, Доротея (ред.), Proc. 14-й Международный. Симп. Рисование графика (GD'06) , LNCS, vol. 4372, Springer-Verlag, стр. 77–88, arXiv : cs.CG/0607113 , doi : 10.1007/978-3-540-70904-6_9 , S2CID   12598338 .
• Ченг, CC; Дункан, Калифорния; Гудрич, Монтана ; Кобуров, С.Г. (1999), «Рисование плоских графов с дугами окружностей», Рисование графов, 7-й Международный симпозиум, GD'99, Замок Штирин, Чешская Республика, 15–19 сентября 1999 г., Труды , Конспекты лекций по информатике , том. 1731, Springer-Verlag, стр. 117–126, doi : 10.1007/3-540-46648-7_12 .
• Дидимо, Уолтер; Идс, Питер ; Лиотта, Джузеппе (2009), «Рисование графиков с пересечениями под прямым углом», Алгоритмы и структуры данных : 11-й международный симпозиум, WADS 2009, Банф, Канада, 21–23 августа 2009 г. Труды , конспекты лекций по информатике, том. 5664, стр. 206–217, номер документа : 10.1007/978-3-642-03367-4_19 .
• Дункан, Кристиан А.; Эппштейн, Дэвид ; Гудрич, Майкл Т .; Кобуров, Стивен Г.; Нёлленбург, Мартин (2011), «Рисование деревьев с идеальным угловым разрешением и полиномиальной площадью», Брандес, Ульрик; Корнельсен, Сабина (ред.), Proc. 18-й Международный. Симп. Рисование графиков , Конспекты лекций по информатике, вып. 6502, Springer-Verlag, стр. 183–194, arXiv : 1009.0581 , doi : 10.1007/978-3-642-18469-7_17 .
• Эппштейн, Д .; Вортман, К. (2011), «Оптимальное угловое разрешение для лице-симметричных рисунков», Журнал графовых алгоритмов и приложений , 15 (4): 551–564, arXiv : 0907.5474 , doi : 10.7155/jgaa.00238 , S2CID   10356432 .
• Финкель, Бенджамин; Тамассиа, Роберто (2005), «Рисование криволинейных графиков методом направленной силы», Рисование графиков, 12-й Международный симпозиум, GD 2004, Нью-Йорк, штат Нью-Йорк, США, 29 сентября – 2 октября 2004 г., Пересмотренные избранные статьи , конспекты лекций в области компьютерных наук, вып. 3383, Springer-Verlag, стр. 448–453, номер документа : 10.1007/978-3-540-31843-9_46 .
• Форман, М.; Хагеруп, Т.; Хараламбидес Дж.; Кауфманн, М.; Лейтон, Флорида ; Симвонис, А.; Вельцль, Э .; Воегингер, Г. (1993), «Рисование графиков на плоскости с высоким разрешением», SIAM Journal on Computing , 22 (5): 1035–1052, doi : 10.1137/0222063 , MR   1237161 .
• Гарг, Ашим; Тамассиа, Роберто (1994), «Плоские чертежи и угловое разрешение: алгоритмы и границы», Алгоритмы, Второй ежегодный европейский симпозиум, Утрехт, Нидерланды, 26–28 сентября 1994 г., Труды , Конспекты лекций по информатике, том. 855, Springer-Verlag, стр. 12–23, doi : 10.1007/BFb0049393 .
• Гарг, Ашим; Тамассиа, Роберто (1995), «О вычислительной сложности тестирования восходящей и прямолинейной планарности», в Тамассиа, Роберто; Толлис, Иоаннис (ред.), Рисование графиков , Конспекты лекций по информатике, том. 894, Springer Berlin/Heidelberg, стр. 286–297, doi : 10.1007/3-540-58950-3_384 .
• Гутвенгер, Карстен; Мутцель, Петра (1998), «Плоские полилинейные рисунки с хорошим угловым разрешением», Рисование графиков (Монреаль, Квебек, 1998) , Конспекты лекций по вычислениям. наук, том. 1547, Берлин: Springer, стр. 167–182, doi : 10.1007/3-540-37623-2_13 , MR   1717450 .
• Халупчок, Иммануэль; Шульц, Андре (2011), «Закрепление воздушных шаров с идеальными углами и оптимальной площадью», Материалы 19-го Международного симпозиума по рисованию графиков .
• Кант, Г. (1996), «Рисование плоских графов с использованием канонического порядка», Algorithmica , 16 (1): 4–32, doi : 10.1007/s004539900035 , hdl : 1874/16676 , MR   1394492 .
• Крамер, Флорика; Крамер, Хорст (2008), «Обзор дистанционной раскраски графов», Discrete Mathematics , 308 (2–3): 422–426, doi : 10.1016/j.disc.2006.11.059 , MR   2378044 .
• Малиц, Сет; Папакостас, Ахиллеас (1994), «Об угловом разрешении плоских графов», SIAM Journal on Discrete Mathematics , 7 (2): 172–183, doi : 10.1137/S0895480193242931 , MR   1271989 .
• Моллой, Майкл; Салаватипур, Мохаммад Р. (2005), «Оценка хроматического числа квадрата плоского графа», Журнал комбинаторной теории , серия B, 94 (2): 189–213, doi : 10.1016/j.jctb. 2004.12.005 , ХДЛ : 1807/9473 , МР   2145512 .