Квип

В информатике queap — это приоритетной очереди структура данных . Структура данных позволяет вставлять и удалять произвольные элементы, а также извлекать элемент с наивысшим приоритетом. Каждое удаление занимает амортизированное время , логарифмическое от количества элементов, которые находились в структуре дольше, чем удаленный элемент. Вставки занимают постоянное амортизированное время.

Структура данных состоит из двусвязного списка и 2–4 древовидной структуры данных, каждая из которых модифицирована для отслеживания своего элемента с минимальным приоритетом. Основная операция структуры — сохранять вновь вставленные элементы в двусвязном списке до тех пор, пока удаление не приведет к удалению одного из элементов списка, после чего все они перемещаются в дерево 2–4. Дерево 2–4 хранит свои элементы в порядке вставки, а не в более традиционном порядке с сортировкой по приоритету.

И структура данных, и ее название были придуманы Джоном Яконо и Стефаном Лангерманом . ^[1]

Описание

queap — это приоритетная очередь, которая вставляет элементы за амортизированное время O (1) и удаляет минимальный элемент за O (log( k + 2)), если есть k элементов, которые находились в куче дольше, чем элемент. быть извлеченным. У queap есть свойство, называемое свойством очереди: время поиска элемента x равно O(lg q ( x )), где q ( x ) равно n - 1 - w ( x ), а w ( x ) — число отдельных элементов, к которым осуществлялся доступ с помощью таких операций, как поиск, вставка или удаление. q ( x ) определяется как количество элементов, к которым не было доступа с момента . последнего доступа x Действительно, свойство очереди является дополнением свойства рабочего набора дерева расширения: время поиска элемента x равно O (lg w ( x )).

Queap может быть представлен двумя структурами данных: двусвязным списком и модифицированной версией 2–4-дерева. Двусвязный список L используется для серии операций вставки и поиска. queap сохраняет указатель на минимальный элемент, хранящийся в списке. Чтобы добавить элемент x в список l , элемент x добавляется в конец списка, а битовая переменная в элементе x устанавливается в единицу. Эта операция выполняется для определения того, находится ли элемент в списке или в дереве 2–4.

Дерево 2–4 используется при выполнении операции удаления. Если элемент x уже находится в дереве T , элемент удаляется с помощью операции удаления дерева 2–4. В противном случае элемент x находится в списке L (выполняется путем проверки, установлена ли битовая переменная). Все элементы, хранящиеся в списке L, затем добавляются к дереву 2–4, при этом битовая переменная каждого элемента устанавливается равной нулю. x затем удаляется из T .

Queap использует только 2–4 свойства древовидной структуры, а не дерево поиска. Модифицированная древовидная структура 2–4 выглядит следующим образом. Предположим, список L имеет следующий набор элементов: $x_{1},x_{2},x_{3},\dots ,x_{k}$ . Когда вызывается операция удаления, набор элементов, хранящихся в L , затем добавляется к листьям дерева 2–4 в этом порядке, после чего добавляется фиктивный лист, содержащий бесконечный ключ. Каждый внутренний узел T имеет указатель $h_{v}$ , который указывает на наименьший элемент в поддереве v . Каждый внутренний узел на пути P от корня до $x_{0}$ есть указатель $c_{v}$ , который указывает на наименьший ключ в $T-T_{v}-\{r\}$ . $h_{v}$ указатели каждого внутреннего узла на пути P игнорируются. Quap имеет указатель на $c_{x_{0}}$ , который указывает на наименьший элемент в T .

Приложение quaps включает в себя уникальный набор событий с высоким приоритетом и извлечение события с самым высоким приоритетом для обработки.

Операции

Пусть minL — указатель, указывающий на минимальный элемент в двусвязном списке L , $c_{x_{0}}$ — минимальный элемент, хранящийся в дереве 2–4, T , k — количество элементов, хранящихся в , а n — общее количество элементов, хранящихся в queap Q. T Операции заключаются в следующем:

New(Q): Инициализирует новый пустой квап.

Инициализируйте пустой двусвязный список L и 2–4- T. дерево Установите k и n равными нулю.

Insert(Q, x): добавьте элемент x в queap Q .

элемент x в список L. Вставьте Установите бит в элементе x что элемент находится в списке L. в единицу, чтобы продемонстрировать , Обновите указатель minL , если x — наименьший элемент в списке. Увеличьте n на 1.

Минимум(Q): получить указатель на наименьший элемент из Q. queap

Если ключ (минл) < ключ (

c_{x_{0}}

), верните минЛ . В противном случае верните

c_{x_{0}}

.

Удалить(Q, x): удалить элемент x из queap Q .

Если бит элемента x установлен в единицу, элемент сохраняется в L. списке Добавьте все элементы от L до T , установив бит каждого элемента равным нулю. Каждый элемент добавляется к родительскому элементу самого правого дочернего элемента T с помощью операции вставки дерева 2–4. L становится пустым. Обновлять

h_{v}

указатели для всех узлов v, чьи дочерние элементы являются новыми/измененными, и повторяйте процесс со следующим родителем, пока родительский элемент не станет равным корню. Прогулка от корня к узлу

x_{0}

и обновите

c_{v}

ценности. Установите k равным n .

Если бит элемента x установлен в ноль, x является листом T . Удалите x, используя операцию удаления дерева 2–4. Начиная с узла x , пройдите по T до узла

x_{0}

, обновление

h_{v}

и

c_{v}

указатели. Уменьшите n и k на 1.

DeleteMin(Q): и вернуть наименьший элемент из queap Q. Удалить

Вызовите операцию минимума (Q) . Операция возвращает мин . Вызовите операцию Удалить(Q, min) . Возврат мин .

CleanUp(Q): все элементы в списке L и дереве T. удалить

Начиная с первого элемента в списке L , пройдите по списку, удаляя каждый узел.

Начиная с корня дерева T , пройдите по дереву, используя алгоритм пост-порядкового обхода , удаляя каждый узел в дереве.

Анализ

Время работы анализируется с помощью амортизированного анализа . Потенциальная функция для queap Q будет равна $\phi (Q)=c|L|$ где $Q=(T,L)$ .

Insert(Q, x): Стоимость операции равна O(1) . Размер списка L увеличивается на единицу, потенциал увеличивается на некоторую константу c .

Минимум(Q): операция не меняет структуру данных, поэтому амортизированная стоимость равна фактической стоимости O(1).

Удалить(Q, x): есть два случая.

Случай 1

Если x находится в дереве T , то амортизированная стоимость не изменяется. Операция удаления представляет собой O(1) амортизированное дерево 2–4 . Поскольку x был удален из дерева, $h_{v}$ и $c_{v}$ указатели могут нуждаться в обновлении. В лучшем случае будет $O(lgq(x))$ обновления.

Случай 2

Если x находится в списке L все элементы из L вставляются в T. , то Это имеет стоимость $a|L|$ некоторой константы a , амортизированной по дереву 2–4. После установки и обновления $h_{v}$ и $c_{v}$ указателей, общее затраченное время ограничено $2a|L|$ . Вторая операция — удалить x из T и пройти путь от x до $x_{0}$ , исправляя $h_{v}$ и $c_{v}$ ценности. Время тратится максимум $2a|L|+O(lgq(x))$ . Если $c>2a$ , то амортизированная стоимость составит $O(lgq(x))$ . Удалить(Q, x): сложение амортизированной стоимости минимума(Q) и Удалить(Q, x) , что $O(lgq(x))$ .

Пример кода

Небольшая Java- реализация queap:

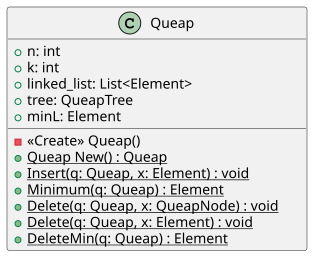
public class Queap
{
    public int n, k;
    public List<Element> l; // Element is a generic data type.
    public QueapTree t;     // a 2-4 tree, modified for Queap purpose
    public Element minL;

    private Queap() {
        n = 0;
        k = 0;
        l = new LinkedList<Element>();
        t = new QueapTree();
    }

    public static Queap New() {
        return new Queap();
    }

    public static void Insert(Queap Q, Element x) {
        if (Q.n == 0)
            Q.minL = x;
        Q.l.add(x);
        x.inList = true;
        if (x.compareTo(Q.minL) < 0)
            Q.minL = x;
    }

    public static Element Minimum(Queap Q) {
        // t is a 2-4 tree and x0, cv are tree nodes.
        if (Q.minL.compareTo(Q.t.x0.cv.key) < 0)
            return Q.minL;

        return Q.t.x0.cv.key;
    }

    public static void Delete(Queap Q, QueapNode x) {
        Q.t.deleteLeaf(x);
        --Q.n;
        --Q.k;
    }

    public static void Delete(Queap Q, Element x) {
        QueapNode n;
        if (x.inList) {
            // set inList of all the elements in the list to false
            n = Q.t.insertList(Q.l, x);
            Q.k = Q.n;
            Delete(Q, n);
        }
        else if ((n = Q.t.x0.cv).key == x)
            Delete(Q, n);
    }

    public static Element DeleteMin(Queap Q) {
        Element min = Minimum(Q);
        Delete(Q, min);
        return min;
    }
}

См. также

Ссылки

^ Яконо, Джон ; Лангерман, Стефан (2005). «Квапс». Алгоритмический . 42 (1). Спрингер: 49–56. дои : 10.1007/s00453-004-1139-5 . S2CID 263883421 .

[1] Яконо, Джон ; Лангерман, Стефан (2005). «Квапс». Алгоритмический . 42 (1). Спрингер: 49–56. дои : 10.1007/s00453-004-1139-5 . S2CID 263883421 .

[1]