Центрированное дерево
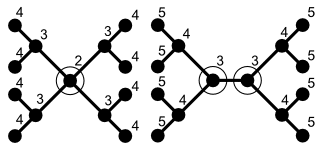
В математическом разделе теории графов центрированное дерево — это дерево только с одним центром , а бицентрированное дерево — это дерево с двумя центрами.
Для графа эксцентриситет вершины v определяется как наибольшее расстояние от v до любой другой вершины. Центром минимальным графа является вершина с эксцентриситетом . Граф может иметь произвольное количество центров. Однако Джордан (1869) доказал, что для деревьев есть только две возможности:
- Дерево имеет ровно один центр (центрированные деревья).
- Дерево имеет ровно два центра (бицентрические деревья). В этом случае два центра соседствуют.
Доказательство этого факта дает, например, Харари. [1]
Примечания
[ редактировать ]- ^ ( Харари, 1969 ), Теорема 4.2.
Ссылки
[ редактировать ]- Джордан, Камилла (1869). «Сюр-ле-сборки линий» . Журнал чистой и прикладной математики (на французском языке). 70 (2): 185–190.
- Харари, Фрэнк (1969). Теория графов . Аддисон-Уэсли Профессионал.
Внешние ссылки
[ редактировать ]- Вайсштейн, Эрик В. «Двуцентровое дерево» . Математический мир .
- Вайсштейн, Эрик В. «Центрированное дерево» . Математический мир .
 | Эта теории графов статья, посвященная , незавершена . Вы можете помочь Википедии, расширив ее . |