Прочность на изгиб

Прочность на изгиб – это напряжение при разрушении при изгибе. Оно равно или немного превышает напряжение разрушения при растяжении.

Прочность на изгиб , также известная как модуль прочности на разрыв , или прочность на изгиб , или прочность на поперечный разрыв , представляет собой свойство материала, определяемое как напряжение в материале непосредственно перед тем, как он поддается испытанию на изгиб. Чаще всего используется испытание на поперечный изгиб, при котором образец, имеющий круглое или прямоугольное поперечное сечение, сгибают до разрушения или текучести с использованием метода испытания на трехточечный изгиб . Прочность на изгиб представляет собой наибольшее напряжение, испытываемое в материале в момент его текучести. Оно измеряется в единицах напряжения, обозначенного здесь символом $\sigma$.

Введение

Рис. 1 – Балка материала при изгибе. Крайние волокна в точках B (сжатие) и A (растяжение).

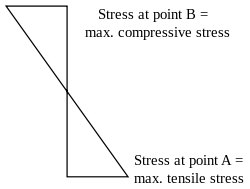
Рис. 2 – Распределение напряжений по толщине балки

Когда объект, изготовленный из одного материала, например деревянная балка или стальной стержень, сгибается (рис. 1), он испытывает ряд напряжений по глубине (рис. 2). На краю объекта на внутренней стороне изгиба (вогнутая грань) напряжение будет иметь максимальное значение сжимающего напряжения. На внешней стороне изгиба (выпуклая поверхность) напряжение будет иметь максимальное значение растяжения. Эти внутренние и внешние края балки или стержня известны как «крайние волокна». Большинство материалов обычно разрушаются при растягивающем напряжении раньше, чем при сжимающем напряжении.

Прочность на изгиб и растяжение

Прочность на изгиб была бы такой же, как прочность на растяжение, если бы материал был однородным . Фактически, большинство материалов имеют небольшие или большие дефекты, которые локально концентрируют напряжения, эффективно вызывая локальную слабость. Когда материал сгибается, только крайние волокна подвергаются наибольшему напряжению, поэтому, если эти волокна не имеют дефектов, прочность на изгиб будет контролироваться прочностью этих неповрежденных «волокон». Однако если один и тот же материал подвергался только растягивающим усилиям, то все волокна в материале находятся под одинаковым напряжением, и разрушение начнется, когда самое слабое волокно достигнет своего предельного растягивающего напряжения. Поэтому прочность на изгиб обычно превышает прочность на растяжение для того же материала. И наоборот, однородный материал с дефектами только на поверхности (например, из-за царапин) может иметь более высокую прочность на растяжение, чем прочность на изгиб.

Если не принимать во внимание какие-либо дефекты, то ясно, что материал разрушится под действием изгибающей силы, меньшей соответствующей растягивающей силы. Обе эти силы будут вызывать одинаковое напряжение разрушения, величина которого зависит от прочности материала.

Для прямоугольного образца результирующее напряжение под действием осевой силы определяется следующей формулой:

$\sigma ={\frac {F}{bd}}$

Это напряжение не является истинным напряжением, поскольку сечение образца считается неизменным ( техническое напряжение ).

• $F$ — осевая нагрузка (сила) в точке разрушения
• $b$ ширина
• $d$ это глубина или толщина материала

Результирующее напряжение для прямоугольного образца под нагрузкой в ​​схеме трехточечного изгиба (рис. 3) определяется формулой, приведенной ниже (см. «Измерение прочности на изгиб»).

Уравнение этих двух напряжений (разрушений) дает:

$\sigma ={\frac {3FL}{2bd^{2}}}$

Обычно L (длина пролета опоры) значительно больше d, поэтому дробь ${\frac {3L}{2d}}$ больше единицы.

Измерение прочности на изгиб

Рис. 3 – Балка при трехточечном изгибе

Для прямоугольного образца под нагрузкой в ​​схеме трехточечного изгиба (рис. 3), начиная с классической формы максимального напряжения изгиба:

$\sigma ={\frac {Mc}{I}}$

• M – момент в луче
• c — максимальное расстояние от нейтральной оси до самого дальнего волокна в плоскости изгиба.
• I — второй момент площади

Для простой опорной балки, показанной на рис. 3, при условии, что нагрузка сосредоточена между опорами, максимальный момент приходится на центр и равен:

$M=P\times r=\left({\frac {F}{2}}\right)\times \left({\frac {L}{2}}\right)={\frac {FL}{4}}$

Для прямоугольного сечения,

$c={\frac {1}{2}}d$ (центральная ось до самого дальнего волокна прямоугольника)

$I={\frac {1}{12}}bd^{3}$ (Второй момент площади прямоугольника)

Объединив эти члены вместе в классическом уравнении напряжения изгиба:

$\sigma =Mc\left({\frac {1}{I}}\right)=\left({\frac {FL}{4}}\right)\left({\frac {d}{2}}\right)\left({\frac {12}{bd^{3}}}\right)$

$\sigma ={\frac {3FL}{2bd^{2}}}$

• F — нагрузка (сила) в точке разрушения (Н)
• L – длина пролета опоры
• б — ширина
• d - толщина

Для прямоугольного образца под нагрузкой при четырехточечном изгибе, при котором пролет нагрузки составляет одну треть пролета опоры:

$\sigma ={\frac {FL}{bd^{2}}}$

• F – нагрузка (сила) в точке разрушения.
• L – длина опорного (наружного) пролета.
• б — ширина
• d - толщина

Для конструкции изгиба 4 точки, если пролет нагрузки составляет 1/2 пролета опоры (т. е. L _i = 1/2 L на рис. 4):

$\sigma ={\frac {3FL}{4bd^{2}}}$

Если пролет нагрузки не составляет ни 1/3, ни 1/2 пролета опоры для установки с изгибом 4 точки (рис. 4):

Рис. 4 – Балка при четырехточечном изгибе

$\sigma ={\frac {3F(L-L_{i})}{2bd^{2}}}$

• L _i – длина погрузочного (внутреннего) пролета

См. также

• Уравнение пучка Эйлера – Бернулли
• Модуль упругости при изгибе
• Испытание на трехточечный изгиб
• Четырехточечное испытание на изгиб

Ссылки

• Дж. М. Ходжкинсон (2000), Механические испытания усовершенствованных волокнистых композитов , Кембридж: Woodhead Publishing, Ltd., стр. 132–133.
• Уильям Д. Каллистер-младший, Материаловедение и инженерия , Хокен: John Wiley & Sons, Inc., 2003.
• ASTM C1161-02c(2008)e1, Стандартный метод испытаний прочности на изгиб усовершенствованной керамики при температуре окружающей среды, ASTM International, Вест-Коншохокен, Пенсильвания.