Склон Один

Slope One — это семейство алгоритмов, используемых для совместной фильтрации , представленное в статье 2005 года Дэниелом Лемиром и Анной Маклахлан. Возможно, это простейшая форма нетривиальной совместной фильтрации по элементам на основе рейтингов. Их простота позволяет особенно легко их эффективно реализовать, а их точность часто находится на одном уровне с более сложными и дорогостоящими алгоритмами. Они также использовались в качестве строительных блоков для улучшения других алгоритмов. Они являются частью основных библиотек с открытым исходным кодом, таких как Apache Mahout и Easyrec .

Совместная фильтрация рейтинговых ресурсов на основе элементов и переоснащение

Когда доступны рейтинги элементов, например, когда людям предоставляется возможность выбора рейтинговых ресурсов (например, от 1 до 5), совместная фильтрация направлена ​​​​на прогнозирование оценок одного человека на основе его прошлых оценок и ( большая) база данных рейтингов, предоставленных другими пользователями.

Пример : Можем ли мы предсказать оценку, которую человек дал бы новому альбому Селин Дион, учитывая, что он поставил «Битлз» 5 из 5?

В этом контексте совместная фильтрация на основе элементов прогнозирует рейтинги одного элемента на основе оценок другого элемента, обычно с использованием линейной регрессии ( $f(x)=ax+b$). Следовательно, если имеется 1000 элементов, можно изучить до 1 000 000 линейных регрессий и, следовательно, до 2 000 000 регрессоров. Этот подход может страдать от серьезной переобучения если только мы не выберем только те пары элементов, по которым несколько пользователей оценили оба элемента.

Лучшей альтернативой может быть изучение более простого предиктора, такого как $f(x)=x+b$: эксперименты показывают, что этот более простой предиктор (называемый Slope One) иногда превосходит линейная регрессия при наличии половины числа регрессоров. Этот упрощенный подход также снижает требования к хранилищу и задержку.

Совместная фильтрация на основе элементов — это лишь одна из форм совместной фильтрации . Другие альтернативы включают совместную фильтрацию на основе пользователей, где вместо этого представляют интерес отношения между пользователями. Однако совместная фильтрация на основе элементов особенно масштабируема в зависимости от количества пользователей.

Совместная фильтрация статистики покупок по позициям

Нам не всегда ставят оценки: когда пользователи предоставляют только бинарные данные (куплен товар или нет), то Slope One и другие алгоритм на основе рейтинга не применяется . Примеры совместной фильтрации на основе двоичных элементов включают Amazon «от элемента к элементу» . запатентованный алгоритм который вычисляет косинус между двоичными векторами, представляющими покупки в матрице пользовательских товаров.

Будучи, возможно, более простым, чем даже Slope One, алгоритм Item-to-Item предлагает интересный ориентир. Рассмотрим пример.

Пример статистики покупок

Клиент	Пункт 1	Пункт 2	Пункт 3
Джон	Купил это	Не купил это	Купил это
Отметка	Не купил это	Купил это	Купил это
Люси	Не купил это	Купил это	Не купил это

В данном случае косинус между пунктами 1 и 2 равен:

${\frac {(1,0,0)\cdot (0,1,1)}{\Vert (1,0,0)\Vert \Vert (0,1,1)\Vert }}=0$,

Косинус между пунктами 1 и 3 равен:

${\frac {(1,0,0)\cdot (1,1,0)}{\Vert (1,0,0)\Vert \Vert (1,1,0)\Vert }}={\frac {1}{\sqrt {2}}}$,

Тогда как косинус между пунктами 2 и 3 равен:

${\frac {(0,1,1)\cdot (1,1,0)}{\Vert (0,1,1)\Vert \Vert (1,1,0)\Vert }}={\frac {1}{2}}$.

Следовательно, пользователь, посещающий элемент 1, получит элемент 3 в качестве рекомендации, пользователь, посещающий элемент 2, получит элемент 3 в качестве рекомендации и, наконец, пользователь, посещающий элемент 3, получит элемент 1 (а затем элемент 2) в качестве рекомендации. Для выдачи рекомендаций модель использует один параметр для каждой пары элементов (косинус). Следовательно, если имеется n до n(n-1)/2 элементов, необходимо вычислить и сохранить косинусов.

Совместная фильтрация по наклону 1 для рейтинговых ресурсов

Чтобы радикально уменьшить переобучение , повысить производительность и упростить реализацию, Slope One на основе рейтингов и элементов совместной фильтрации было предложено семейство легко реализуемых алгоритмов . По сути, вместо использования линейной регрессии оценок одного элемента к рейтингам другого элемента ( $f(x)=ax+b$), он использует более простую форму регрессии с одним свободным параметром ( $f(x)=x+b$). В этом случае бесплатный параметр представляет собой просто среднюю разницу между рейтингами двух элементов. Было показано, что в некоторых случаях он намного точнее, чем линейная регрессия. и это занимает половину памяти или меньше.

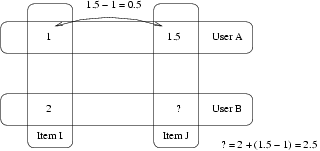
Пример :

1. Пользователь А поставил 1 баллу I и 1,5 балла J.
2. Пользователь Б поставил 2 балла за пункт I.
3. Как вы думаете, как пользователь Б оценил предмет J?
4. Первый вариант ответа — сказать 2,5 = 2+1,5-1.

В качестве более реалистичного примера рассмотрим следующую таблицу.

Пример базы рейтингов

Клиент	Пункт А	Пункт Б	Пункт С
Джон	5	3	2
Отметка	3	4	Не оценил
Люси	Не оценил	2	5

В этом случае средняя разница в рейтингах между пунктом Б и А составляет (-2+1)/2 = -0,5. Следовательно, в среднем предмет А оценивается выше пункта В на 0,5. Аналогично, средняя разница между товарами C и A равна -3. Следовательно, если мы попытаемся предсказать рейтинг Люси по элементу A, используя ее рейтинг по элементу B, мы получим 2+0,5 = 2,5. Аналогично, если мы попытаемся предсказать ее рейтинг по предмету А, используя ее рейтинг по предмету С, мы получим 5+3 = 8.

Если пользователь оценил несколько элементов, прогнозы просто объединяются с использованием средневзвешенного значения, где хорошим выбором веса является количество пользователей, оценивших оба элемента. В приведенном выше примере и Джон, и Марк оценили элементы A и B, следовательно, вес 2, и только Джон оценил оба элемента A и C, следовательно, вес 1, как показано ниже. мы бы прогнозировали следующую оценку Люси по пункту A:

${\frac {2\times 2.5+1\times 8}{2+1}}={\frac {13}{3}}=4.33$

Следовательно, для реализации первого наклона для данных n элементов все, что необходимо, — это вычислить и сохранить средние различия и количество общих оценок для каждого из n элементов. ² пары предметов.

Алгоритмическая сложность Slope One

Предположим, что имеется n элементов, m пользователей и N оценок. Для расчета средних разностей рейтингов для каждой пары предметов требуется до n(n-1)/2 единиц хранения и до mn ² временные шаги. Эта вычислительная оценка может быть пессимистической: если мы предположим, что пользователи оценили до y элементов, то можно вычислить различия не более чем в n ² + мой ² . Если пользователь ввел x оценок, для прогнозирования одного рейтинга требуется x шагов времени, а для прогнозирования всех его недостающих оценок требуется до ( nx ) x шагов времени. Обновление базы данных, когда пользователь уже ввел x оценок и вводит новый, требует x шагов времени.

Можно уменьшить требования к хранению, разделив данные (см. Раздел (база данных) ) или используя разреженное хранилище: пары элементов, не имеющих (или имеющих мало) пользователей, объединяющих пользователей, могут быть опущены.