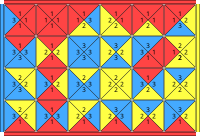
Площади Мак-Магона

Частное решение; это иллюстрирует ограничение B _20,0,0 , которое требует использования одного цвета по периметру, а также максимизирует наибольшую непрерывную одноцветную область внутри периметра.

Квадраты Мак-Магона — это головоломка с сопоставлением ребер, впервые опубликованная Перси Мак-Махоном в 1921 году. использование 24 уникальных квадратов с 3-х цветными узорами; каждому из четырех ребер присвоен один цвет. Полный набор из 24 квадратов расположен рядом друг с другом путем сопоставления цветов краев , образуя сетку 4 на 6 . Такие головоломки с мозаикой имеют несколько вариантов, которые определяются ограничениями на расположение 24 квадратов. Эта игра также коммерциализировалась в различных физических формах различными компаниями.

Игра

Все 24 квадрата Мак-Магона, перерисованные с рис. 26 из книги «Новые математические игры» (Мак-Магон, 1921 г.).

Квадраты Мак-Магона были впервые опубликованы в Перси Александра Мак-Магона трактате «Новые математические игры» в 1921 году . Первоначальная версия состояла из одной копии каждого из 24 различных квадратов, которые можно было сделать, раскрасив края квадрата в один из трех цветов. (Здесь «разные» означает с точностью до вращения.) Цель состоит в том, чтобы расположить квадраты в сетку 4 на 6 так, чтобы, когда два квадрата имеют общий край, общий край в обоих квадратах был одного цвета.

В 1964 году с помощью суперкомпьютера было получено 12 261 решение базовой версии головоломки «Квадраты Мак-Магона», время выполнения которой составило около 40 часов.

Квадраты Мак-Магона (3 цвета)

Один цвет	Два цвета						Три цвета
Четверные квадрицепсы	тройки			Парный разряд			Парный разряд
1111	1112	1113		1122	1133		1123	1132	1213
2222	1222		2223	1212		2233	1223	1322	1232
3333		1333	2333		1313	2323	1233	1332	1323

Теория

Игра «Квадраты Мак-Магона» — пример головоломки с сопоставлением ребер. Семейство таких задач NP-полное . В первой части «Новых математических развлечений» эти игры описаны в общих чертах, начиная с линейных форм ( домино ), а затем подробно развиваясь с помощью аналогичных игр с использованием плиток в форме равносторонних треугольников, квадратов, прямоугольных равнобедренных треугольников, кубов и шестиугольников.

Всего имеется 24 различных квадрата для 3 цветов. Для произвольного количества цветов $n$, количество уникальных квадратов можно найти по выражению ${\frac {n}{4}}\cdot (n+1)\cdot (n^{2}-n+2)$.

Для других форм с $n$ цветов, МакМахон определил количество уникальных узоров:

• Треугольник: ${\frac {n}{3}}\cdot (n^{2}+2)$
• Пентагон: ${\frac {n}{5}}\cdot (n^{4}+4)$
• Шестиугольник: ${\frac {n}{6}}\cdot (n+1)\cdot (n^{4}-n^{3}+n^{2}+2)$
• Семиугольник: ${\frac {n}{7}}\cdot (n^{6}+6)$

Например, для треугольника с тремя сторонами, каждой из которых присвоен один из четырех возможных цветов, существует 56 уникальных шаблонов.

Варианты

• Примеры решений квадратов Мак-Магона
• 
  С _1,1,1 Б _10,10,0 (рис. 27)
• 
  С _1,2 Б _20,0,0 (рис. 28)
• 
  С _1,2 Б _12,4,4 (рис. 28)

Контактная система

В своей книге МакМахон предложил возможность определять, какие границы могут соприкасаться друг с другом, на основе их цветов. Это некоторая перестановка трех цветов, описанная C _a,b,c . Здесь a, b и c обозначают сдвиг цветов, которому могут соответствовать первый, второй и третий цвета. «1» соответствует самому себе, а «2» означает, что ему должен быть сопоставлен другой цвет.

Например, C _1,1,1 представляет собой 1 к 1, 2 к 2 и 3 к 3, поскольку каждое из этих совпадений представлено числом 1. Альтернативно, C _1,2 представляет собой 1 к 1 и 2 к 3 как совпадение 1 к 1 обозначается цифрой 1, а совпадение 2 и 3 обозначается цифрой 2. Аналогичным образом можно описать и другие цвета. Например, раскраска C _1,2,2,2 представляет собой числа от 1 до 1, от 2 до 3, от 4 до 5 и от 6 до 7.

Отсюда мы видим, что единственные возможные числа для описания пар — это 1 и 2, поскольку число 3 или выше просто пропускает цвет, который в противном случае использовался бы так же, поскольку раскраски относительны .

Границы

Другой способ изменить головоломку — ограничить цвета в квадратах, составляющие цвета границ. В классической головоломке с квадратами Мак-Магона на границе всего 20 мест. Количество каждого цвета, которое может присутствовать в этих 20 местах, можно описать как B _a,b,c. где a, b и c — количество элементов границы каждого цвета.

Например, B _20,0,0 представляет 20 единиц первого цвета и ни одного остального, поскольку первый цвет уже занимает все доступные граничные пространства. Альтернативно, B _10,10,0 представляет 10 первого цвета и 10 следующего. Подобным образом можно описать и другие цвета. Например, граница B _22,16,8,2 представляет 22 первых, 16 вторых, 8 следующих и 2 последних цвета для заполнения цветов границы.

Отсюда мы видим, что единственными возможными числами для описания количества каждого цвета, составляющего границу, являются четные числа, поскольку это подразумевало бы нечетное количество другого цвета, что нарушало бы четность общего числа треугольников.

Аналогичные головоломки

MacMahon Squares вместе с вариациями этой идеи были коммерциализированы как Multimatch.

Еще одна головоломка с похожими свойствами — «Кубики Мак-Магона», представляющие собой набор из 30 кубиков со сторонами, окрашенными в один из 6 разных цветов. В отличие от головоломки «Квадраты Мак-Магона», мы не включаем все 2226 возможных кубиков, а только кубики, содержащие ровно 6 различных цветов и по одному каждого из 6 цветов.

Квадраты Мак-Магона послужили основой для множества других головоломок. Некоторые из них включают «Загадку Нельсона», плитка Ванга и ТетраВекс .

В коммерческой настольной игре Trioker , запатентованной в 1969 году Марком Одье, используются треугольные плитки, впервые предложенные МакМахоном в 1921 году.

Внешние ссылки

1. Площади Мак-Магона онлайн