Смешанный график

В теории графов смешанный граф $G = (V, E, A)$ — это граф , состоящий из набора вершин $V$ набора (неориентированных) ребер $E$ и набора направленных ребер (или дуг) $A.$ , ^[1]

Определения и обозначения

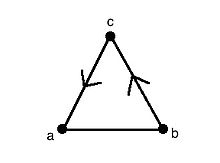
Рассмотрим соседние вершины $u,v\in V$ . , Направленное ребро называемое дугой , представляет собой ребро с ориентацией и может быть обозначено как ${\overrightarrow {uv}}$ или $(u,v)$ (Обратите внимание, что $u$ это хвост и $v$ является главой дуги). ^[2] Кроме того, ненаправленное ребро или ребро — это ребро без ориентации и может быть обозначено как $uv$ или $[u,v]$ . ^[2]

В нашем примере мы не будем рассматривать петли или кратные ребра смешанных графов.

Блуждание по смешанному графу – это последовательность $v_{0},c_{1},v_{1},c_{2},v_{2},\dots ,c_{k},v_{k}$ вершин и ребер/дуг таких, что для каждого индекса $i$ , или $c_{i}=v_{i}v_{i+1}$ является ребром графа или $c_{i}={\overrightarrow {v_{i}v_{i+1}}}$ является дугой графа. Этот обход является путем, если он не повторяет никаких ребер, дуг или вершин, за исключением, возможно, первой и последней вершин. Маршрут называется замкнутым , если его первая и последняя вершины совпадают, а замкнутый путь является циклом . Смешанный граф называется ациклическим, если он не содержит циклов.

Раскраска

Раскраску смешанного графа можно рассматривать как маркировку или присвоение $k$ различных цветов (где $k$ — положительное целое число) вершинам смешанного графа. ^[3] Вершинам, соединенным ребром, необходимо назначить разные цвета. Цвета могут быть представлены числами от $1$ до $k$ , а для направленной дуги хвост дуги должен быть окрашен в меньшее число, чем начало дуги. ^[3]

Пример

Например, рассмотрим рисунок справа. Наши доступные $k$ -цвета для раскраски смешанного графа: ${1, 2, 3}.$ Поскольку $u$ и $v$ соединены ребром, они должны иметь разные цвета или маркировку ( $u$ и $v$ имеют метки 1 и 2 соответственно). У нас также есть дуга от $v$ до $w$ . Поскольку ориентация задает порядок, мы должны пометить хвост ( $v$ ) меньшим цветом (или целым числом из нашего набора), чем начало ( $w$ ) нашей дуги.

Сильная и слабая окраска.

k (Сильная) правильная $-раскраска$ смешанного графа — это функция $c : V \to [k]$ где $[k] := {1, 2, \dots, k}$ такая, что $c (u) \neq c (v),$ если $uv \in E$ и $c (u) < c (v)$ , если ${\overrightarrow {uv}}\in A$ . ^[1]

Можно применить более слабое условие к нашим дугам, и мы можем рассматривать слабую собственную $k$ -раскраску смешанного графа как функцию $c : V \to [k],$ где $[k] := {1, 2, \dots, k},$ такую что $c (ты) \neq c (v),$ если $uv \in E$ и $c (ты) \leq c (v)$ , если ${\overrightarrow {uv}}\in A$ . ^[1] Возвращаясь к нашему примеру, это означает, что мы можем пометить как начало, так и хвост $(v, w)$ положительным целым числом 2.

Подсчет

Раскраска может существовать, а может и не существовать для смешанного графа. Чтобы смешанный граф имел $k$ -раскраску, в нем не должно быть ориентированных циклов. ^[2] Если такая $k$ -раскраска существует, то мы ссылаемся на наименьшее $k,$ необходимое для правильной раскраски нашего графа, как на хроматическое число , обозначаемое $χ (G)$ . ^[2] Число собственных $k$ -раскрасок является полиномиальной функцией от $k,$ называемой хроматическим многочленом нашего графа $G$ (по аналогии с хроматическим многочленом неориентированных графов) и может быть обозначено $χ G (k)$ . ^[1]

Вычисление слабых хроматических полиномов

Метод удаления-сокращения можно использовать для вычисления слабых хроматических полиномов смешанных графов. Этот метод включает в себя удаление (т. е. удаление) ребра или дуги и, возможно, соединение оставшихся вершин, инцидентных этому ребру или дуге, для формирования одной вершины. ^[4] После удаления ребра $e$ из смешанного графа $G = (V, E, A)$ мы получаем смешанный граф $(V, E - e, A)$ . Обозначим это удаление ребра $e$ через $G - e$ . Аналогично, удаляя дугу $a$ из смешанного графа, мы получаем $(V, E, A - a)$ , где мы обозначаем удаление $a$ через $G - a$ . Кроме того, мы обозначаем сжатие $e$ и $a$ через $G / e$ и $G / a$ соответственно. Из предложений, приведенных в Beck et al. ^[4] мы получаем следующие уравнения для вычисления хроматического полинома смешанного графа: ^[5]

$\chi _{G}(k)=\chi _{G-e}(k)-\chi _{G/e}(k)$ ,
$\chi _{G}(k)=\chi _{G-a}(k)+\chi _{G/a}(k)-\chi _{G_{a}}(k)$ .

Приложения

Проблема планирования

Смешанные графы могут использоваться для моделирования задач планирования цеха , в которых необходимо выполнить набор задач с учетом определенных временных ограничений. В задачах такого типа ненаправленные ребра можно использовать для моделирования ограничения, заключающегося в несовместимости двух задач (они не могут выполняться одновременно). Направленные ребра можно использовать для моделирования ограничений приоритета, при которых одна задача должна выполняться раньше другой. Граф, определенный таким образом из задачи планирования, называется дизъюнктивным графом . Задача о раскраске смешанного графа может быть использована для нахождения расписания минимальной длины для выполнения всех задач. ^[2]

Байесовский вывод

Смешанные графы также используются в качестве графических моделей для байесовского вывода . В этом контексте ациклический смешанный граф (без циклов направленных ребер) также называется цепным графом . Направленные ребра этих графов используются для обозначения причинно-следственной связи между двумя событиями, при которой исход первого события влияет на вероятность второго события. Вместо этого ненаправленные края указывают на непричинную корреляцию между двумя событиями. Компонента связности неориентированного подграфа цепного графа называется цепью. Цепной граф можно преобразовать в неориентированный граф, построив его моральный граф , неориентированный граф, сформированный из цепного графа путем добавления неориентированных ребер между парами вершин, имеющих исходящие ребра в одну и ту же цепь, а затем забывания ориентации направленных ребер. . ^[6]

Примечания

^ Jump up to: ^а ^б ^с ^д Бек и др. (2013 , стр. 1)
^ Jump up to: ^а ^б ^с ^д ^и Райс (2007 , стр. 1)
^ Jump up to: ^а ^б Хансен, Куплинский и де Верра (1997 , стр. 1)
^ Jump up to: ^а ^б Бек и др. (2013 , стр. 4)
^ Бек и др. (2013 , стр. 5)
^ Коуэлл и др. (1999) .

Ссылки

Бек, М.; Бладо, Д.; Кроуфорд, Дж.; Жан-Луи, Т.; Янг, М. (2013), «О слабых хроматических полиномах смешанных графов», Графы и комбинаторика , arXiv : 1210.4634 , doi : 10.1007/s00373-013-1381-1 .
Коуэлл, Роберт Г.; Дэвид, А. Филип ; Лауритцен, Штеффен Л .; Шпигельхальтер, Дэвид Дж. (1999), Вероятностные сети и экспертные системы: точные методы вычисления для байесовских сетей , Springer-Verlag, Нью-Йорк, стр. 27, номер домена : 10.1007/0-387-22630-3 , ISBN 0-387-98767-3
Хансен, Пьер; Куплинский, Хулио; де Верра, Доминик (1997), «Смешанные раскраски графов», Математические методы исследования операций , 45 (1): 145–160, doi : 10.1007/BF01194253 , MR 1435900 .
Райс, Б. (2007), «Раскраска некоторых классов смешанных графов», Discrete Applied Mathematics , 155 (1): 1–6, doi : 10.1016/j.dam.2006.05.004 , MR 2281351 .

Внешние ссылки

Вайсштейн, Эрик В. «Смешанный граф» . Математический мир .

[BeckBladoCrawfordJeanLouisYoung-1] Jump up to: ^а ^б ^с ^д Бек и др. (2013 , стр. 1)

[Ries-2] Jump up to: ^а ^б ^с ^д ^и Райс (2007 , стр. 1)

[HansenKuplinskydeWerra-3] Jump up to: ^а ^б Хансен, Куплинский и де Верра (1997 , стр. 1)

[BeckBladoCrawfordJeanLouisYoung_a-4] Jump up to: ^а ^б Бек и др. (2013 , стр. 4)

[BeckBladoCrawfordJeanLouisYoung_b-5] Бек и др. (2013 , стр. 5)

[FOOTNOTECowellDawidLauritzenSpiegelhalter1999-6] Коуэлл и др. (1999) .

[1]

[2]

[3]

[4]

[5]

[6]