Направления действий

Направления действий
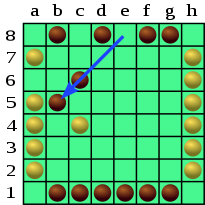
	Начальная позиция линий действия
Дизайнеры	Клод Суси
Жанры	Настольная игра ; Абстрактная стратегическая игра
Игроки	2
Время установки	< 1 минута
Шанс	Никто
Навыки	Стратегия , тактика
Синонимы	ДОСТУПНЫЙ

Lines of Action (или LOA ) — абстрактная стратегическая настольная игра для двух игроков, придуманная Клодом Суси. Цель состоит в том, чтобы соединить все свои фигуры в одну группу. Игра была рекомендована Spiel des Jahres в 1988 году. ^[1]

Правила

Цель

Цель игры — собрать все свои фигуры в единое тело так, чтобы они были соединены по вертикали, горизонтали или диагонали ( 8-связность ). ^{[ нужны разъяснения ]}

Краткое описание движения

Игроки чередуют ходы, первый ход делают черные.
Части перемещаются по горизонтали, вертикали или диагонали.
Фигура перемещается ровно на столько мест, сколько фигур (как дружественных, так и вражеских) находится на линии, по которой она движется. Например, черные могут открыть ход с8-с6. Фигура черных ходит на два хода.

Диаграммы движения

Фигура не может перепрыгивать через фигуру противника. Таким образом, на диаграмме ниже белые не могут сыграть a6-d6, хотя в шестом ряду есть три фигуры. Вместо этого белые могут сыграть a6-c4, перемещаясь на две клетки, потому что на диагонали (a6-f1) есть две фигуры, в которых белые движется.

Фигура может перепрыгивать через свои фигуры. Таким образом, черные могут продолжить ходом e8-b5, перепрыгнув свою фигуру. Он ходит на три клетки, потому что на диагонали (a4-e8), по которой он ходит, есть три фигуры.

Фигура может приземлиться на поле, занятое фигурой противника, в результате чего последняя захватывается и удаляется из игры. Например, белые могут сыграть h3-f1, захватив черные фигуры на f1.

Игрок, который превратился в одну фигуру, выигрывает игру, потому что его фигуры по определению едины. Если ход в результате взятия приводит к тому, что все свои фигуры каждого игрока оказались в непрерывном теле, то либо игрок, сделавший ход, выигрывает, либо игра завершается вничью, в зависимости от правил, действующих на конкретном турнире.

Одновременное подключение

В оригинальном издании «Амбара игр» 1969 года одновременное соединение описывалось как ничья. Во втором издании правила были изменены, чтобы объявить победу передвигающегося игрока. Вот примечание Сида Саксона в предисловии ко второму изданию: «Клод Суси и я — все, что осталось от NYGA. По его просьбе я исправил ошибку в правилах ЛИНИИ ДЕЙСТВИЯ, исключив возможные ничьи». Однако, несмотря на намерение изобретателя LOA, большинство современных турниров, включая чемпионаты мира и олимпиады по интеллектуальным видам спорта, оценивают одновременную связь как ничью.

Стратегия

Игра может стать вполне тактической на открытых позициях, где фигуры с обеих сторон подвижны. Однако стратегическая глубина игры во многом определяется стратегиями блокирования, призванными ограничить мобильность противника. Может быть выгодно прижать одну или несколько фигур противника к краю доски, перемещаясь во втором ряду или столбце.

Наличие большего количества фигур обычно является преимуществом, поскольку они могут ограничить возможности противника, собираясь вместе. С другой стороны, материальные соображения не имеют решающего значения, поскольку меньшее количество частей также означает меньшее количество частей, которые можно объединить.

Пример игры

Вышеупомянутые ходы иллюстрируют правила, но не обязательно хорошую игру. Следующие ходы более типичны для опытной игры.

Черные играют b1-b3. Фигура перемещается на две клетки по вертикали, поскольку в вертикали две фигуры: b1 и b8. Этот ход не дает белым возможности взять взятие и грозит заблокировать фигуры на линии «а».

Белые ходят h4-f2. Фигура перемещается на две клетки, потому что по диагонали находятся две фигуры: h4 и e1. Белые угрожают подвижности черных фигур в нижнем ряду.

Черные играют d1:a4, перепрыгивая через свою фигуру (что разрешено) и захватывая белую фигуру на a4. Обратите внимание, что черные сделали ход на три клетки, так как в диагонали было три фигуры: a4, b3 и d1.

Неясно, выгоден ли захват или нет. У черных теперь есть лишняя фигура, но этот ход не помог белым или создать центральную массу для черных. Обычно ранние захваты на краю не особенно эффективны, тогда как ранние захваты в центре чрезвычайно хороши.

Белые играют h2-e2, продолжая блокаду первой горизонтали. Фигура перемещается на три клетки, перепрыгивая через дружественную фигуру. Белые, несмотря на существенный недостаток хода вторыми, по-видимому, сейчас лидируют из-за пониженной подвижности фигур черных первого ряда. Белые вскоре сыграют a2-d2, продолжая строить свой мост и заставляя черную фигуру на e1 сходить в сторону, если она захочет присоединиться к игре. Черным вряд ли поможет попытка уйти ходом e1-c3, потому что это позволит белым взять взятие ходом a5:c3.

Пример выигрышного хода

На диаграмме ниже белые сделали ход, соединяющий все свои фигуры, в то время как черным еще осталось как минимум два хода до такого состояния. Таким образом, белые выиграли партию.

Чемпионы

Чемпионаты мира проходят ежегодно на Олимпиаде интеллектуальных видов спорта . Чемпионы мира с 1997 года приведены в списке ниже. ^[2]

1997: Фред Кук
1998: Хартмут Тордсен
1999: Фред Кук
2000: Йохен Дрекслер
2001: Коичи Николас
2002: Фред Кук
2003: Коичи Николас
2004: Фред Кук
2005: Коичи Николас
2006: Фред Кук
2007: Тим Хеббес
2008: Джеймс Хеппелл
2009: Тим Хеббес
2010: Андрес Кууск
2011: Тим Хеббес
2012: Питер Хорлок
2013: Анкуш Ханделвал
2014: Ален Декер
2015: Андрес Кууск
2016: Джеймс Хеппелл
2017: Джеймс Хеппелл ^[3]
2018: Андрес Кууск ^[4]
2019: Джеймс Хеппелл ^[5]
2020: Джеймс Хеппелл ^[6]
2021: Андрес Кууск
2022: Коичи Николас
2023: Джеймс Хеппелл

Вариант

Вариант линий действия с другой стартовой позицией также был предложен Суси и известен как Яичница-болтунья . ^[7]

См. также

Список чемпионатов мира по интеллектуальным видам спорта

Ссылки

^ LoA на официальном сайте немецкой игры года.
^ Результаты LOA олимпиады по интеллектуальным видам спорта http://www.boardability.com/result.php?id=lines_of_action, 10 июля 2010 г.
^ Таблица медалей MSO 2017 https://msoworld.com/2017-medal-table/ 18 января 2021 г.
^ Таблица медалей MSO 2018 https://msoworld.com/2018-medal-table/ 18 января 2021 г.
^ Таблица медалей MSO 2019 https://msoworld.com/2019-medal-table/ 18 января 2021 г.
^ Таблица медалей MSO 2020 https://msoworld.com/2020-medal-table/ 18 января 2021 г.
^ http://brainking.com/en/GameRules?tp=86 Веб-страница Brain King: Правила приготовления яичницы-болтуньи

Библиография

Саксон, Сид (1982) [1-й паб. 1969, Рэндом Хаус , Нью-Йорк]. Гамма игр . Книги Пантеона. ISBN 0-394-71115-7 .
Шмиттбергер, Р. Уэйн (1992). Новые правила классических игр . John Wiley & Sons Inc. ISBN 978-0471536215 .

Внешние ссылки

[sdj-1] LoA на официальном сайте немецкой игры года.

[2] Результаты LOA олимпиады по интеллектуальным видам спорта http://www.boardability.com/result.php?id=lines_of_action, 10 июля 2010 г.

[3] Таблица медалей MSO 2017 https://msoworld.com/2017-medal-table/ 18 января 2021 г.

[4] Таблица медалей MSO 2018 https://msoworld.com/2018-medal-table/ 18 января 2021 г.

[5] Таблица медалей MSO 2019 https://msoworld.com/2019-medal-table/ 18 января 2021 г.

[6] Таблица медалей MSO 2020 https://msoworld.com/2020-medal-table/ 18 января 2021 г.

[7] ttp://brainking.com/en/GameRules?tp=86 Веб-страница Brain King: Правила приготовления яичницы-болтуньи

[1]

[2]

[3]

[4]

[5]

[6]

[7]