Древовидный автомат
Древовидный автомат — это тип конечного автомата . Древовидные автоматы имеют дело с древовидными структурами , а не со строками более традиционных конечных автоматов.
В следующей статье рассматриваются автоматы ветвящихся деревьев, соответствующие регулярным языкам деревьев .
Как и классические автоматы, автоматы с конечным деревом (FTA) могут быть как детерминированными автоматами, так и нет. В зависимости от того, как автомат обрабатывает входное дерево, автоматы с конечным деревом могут быть двух типов: (а) снизу вверх, (б) сверху вниз. Это важный вопрос, поскольку, хотя недетерминированные (ND) нисходящие автоматы и ND-автоматы с восходящим движением эквивалентны по выразительной силе, детерминированные нисходящие автоматы строго менее мощны, чем их детерминированные восходящие аналоги, поскольку свойства дерева заданные детерминированными нисходящими древовидными автоматами, могут зависеть только от свойств пути. (Детерминированные автоматы с восходящим деревом столь же мощны, как и автоматы с деревьями ND.)
Определения [ править ]
Конечный древесный автомат снизу вверх над F определяется как набор( Q , F , Q f , Δ),где Q — набор состояний, F — ранжированный алфавит (т. е. алфавит, символы которого имеют ассоциированную арность ), Q f ⊆ Q — набор конечных состояний, а ∆ — набор правил перехода вида f ( q 1 ( x 1 ),..., q n ( x n )) → q ( f ( x 1 ,..., x n )), для n -арного f ∈ F , q , q i ∈ Q и переменные x i , обозначающие поддеревья. То есть члены Δ являются правилами перезаписи узлов, чьи дочерние корни являются состояниями, в узлы, корни которых являются состояниями. Таким образом, состояние узла выводится из состояний его дочерних элементов.
Для n =0, то есть для постоянного символа f , приведенное выше определение правила перехода гласит: f () → q ( f ()); часто для удобства пустые скобки опускаются: f → q ( f ).Поскольку эти правила перехода для постоянных символов (листьев) не требуют состояния, никаких явно определенных начальных состояний не требуется.Древовидный автомат снизу вверх запускается на основном терме над F , начиная со всех его листьев одновременно и двигаясь вверх, связывая состояние выполнения из Q с каждым подтермом.Термин принимается, если его корень связан с принимающим состоянием из Q f . [1]
Конечный древесный автомат сверху вниз над F определяется как набор( Q , F , Q i , Δ),с двумя отличиями от древовидных автоматов снизу вверх. Во-первых, Q i ⊆ Q , множество его начальных состояний, заменяет Q f ; во-вторых, его правила перехода ориентированы обратно: q ( f ( x 1 ,..., x n )) → f ( q 1 ( x 1 ),..., q n ( x n )), для n -арного f ∈ F , q , q i ∈ Q и переменные xi , обозначающие поддеревья.То есть члены Δ здесь переписывают правила с узлов, корни которых являются состояниями, на узлы, чьи дочерние корни являются состояниями.Автомат, работающий сверху вниз, начинается в некоторых из своих начальных состояний в корне и движется вниз по ветвям дерева, индуктивно связывая состояние с каждым подтермом.Дерево считается принятым, если таким образом можно пройти через каждую ветку. [2]
Древовидный автомат называется детерминированным (сокращенно DFTA ), если никакие два правила из Δ не имеют одинаковой левой части; в противном случае его называют недетерминированным ( NFTA ). [3] Недетерминированные нисходящие древовидные автоматы обладают той же выразительной силой, что и недетерминированные восходящие автоматы; [4] правила перехода просто меняются местами, и конечные состояния становятся начальными состояниями.
Напротив, детерминированные нисходящие древовидные автоматы [5] менее эффективны, чем их восходящие аналоги, поскольку в детерминированном древовидном автомате никакие два правила перехода не имеют одинаковой левой части. Для древовидных автоматов правила перехода — это правила перезаписи; а для нисходящих — левая сторона будет родительскими узлами. Следовательно, детерминированный нисходящий древовидный автомат сможет проверять только те свойства дерева, которые истинны во всех ветвях, поскольку выбор состояния для записи в каждую дочернюю ветвь определяется в родительском узле без знания содержимого дочерних ветвей. .
Автоматы с бесконечным деревом расширяют нисходящие автоматы до бесконечных деревьев и могут использоваться для доказательства разрешимости S2S , монадической теории второго порядка с двумя преемниками. Для WS2S достаточно автоматов конечного дерева (недетерминированных, если они работают сверху вниз). [6]
Примеры [ править ]
Автомат снизу вверх, списки логические принимающий
Использование раскраски для различения членов F и Q и использование ранжированного алфавита F ={ ЛОЖЬ , истинный , ноль , минусы (.,.) }, с cons, имеющие арность 2 и все остальные символы, имеющие арность 0, восходящий древовидный автомат, принимающий набор всех конечных списков логических значений, может быть определен как ( Q , F , Q f , Δ) с Q = { Бул , BList }, Q f = { BList } и Δ, состоящий из правил
ЛОЖЬ → Бул ( ЛОЖЬ ) (1), истинный → Бул ( истинный ) (2), ноль → Блист ( ноль ) (3) и минусы ( Бул (x 1 ), BList (x 2 )) → Блист ( минусы (х 1 , х 2 )) (4).
В этом примере правила можно интуитивно понимать как присвоение каждому термину его типа восходящим способом; например, правило (4) можно прочитать как «Термин cons ( x 1 , x 2 ) имеет тип BList при условии, что x 1 и x 2 имеют тип Бул и BList соответственно».Приемлемый пример запуска:
минусы ( ЛОЖЬ , минусы ( истинный , ноль )) ⇒ минусы ( ЛОЖЬ , минусы ( истинный , Блист ( ноль ) )) по (3) ⇒ минусы ( ЛОЖЬ , минусы ( Бул ( истинный ), Блист ( ноль ) )) по (2) ⇒ минусы ( ЛОЖЬ , Блист ( минусы ( истинный , ноль ))) по (4) ⇒ минусы ( Бул ( ЛОЖЬ ), Блист ( минусы ( истинный , ноль ))) по (1) ⇒ Блист ( минусы ( ЛОЖЬ , минусы ( истинный , ноль ))) по (4), принято.
См. вывод того же термина из грамматики регулярного дерева, соответствующей автомату, показанный в Грамматике регулярного дерева#Примеры .
Отклоняющий пример запуска:
минусы ( ЛОЖЬ , истинный ) ⇒ минусы ( ЛОЖЬ , Бул ( истинный ) ) по (1) ⇒ минусы ( Бул ( ЛОЖЬ ), Бул ( истинный ) ) согласно (2), дальнейшее правило не применимо.
Интуитивно это соответствует термину минусы ( ЛОЖЬ , true ) не правильно типизирован.
Нисходящий автомат, принимающий числа, кратные 3, в двоичной записи [ править ]
| (А) | (Б) | (С) | (Д) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Нить грамматика правила | Нить автомат переходы | Дерево автомат переходы | Дерево грамматика правила | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
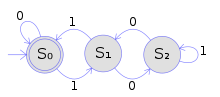 |
Используя ту же раскраску, что и выше, этот пример показывает, как древовидные автоматы обобщают обычные строковые автоматы.Конечный детерминированный строковый автомат, показанный на рисунке, принимает все строки двоичных цифр, которые обозначают кратные 3.Используя понятия из Детерминированного конечного автомата # Формальное определение , он определяется следующим образом:
- множество Q состояний равно { С 0 , С1 , S2 } ,
- входной алфавит равен { 0 , 1 },
- исходное состояние С 0 ,
- набор конечных состояний равен { S 0 } и
- переходы соответствуют значениям, указанным в столбце (B) таблицы.
В настройке древовидного автомата входной алфавит изменяется так, что символы 0 и 1 являются одновременно унарными и нулевыми символами, скажем nil используется для листьев деревьев.Например, двоичная строка " 110 " в настройке струнного автомата соответствует терму " 1 ( 1 ( 0 ( nil )))» в настройке древовидного автомата; таким образом строки можно обобщить до деревьев или термов.Автомат конечного дерева сверху вниз, принимающий набор всех терминов, соответствующих кратным 3 в записи двоичной строки, затем определяется следующим образом:
- множество Q состояний все еще { С 0 , С1 , S2 } ,
- ранжированный входной алфавит равен { 0 , 1 , ноль }, с Арити ( 0 )= Арность ( 1 )=1 и Арность ( ноль )=0, как объяснено,
- набор начальных состояний равен { S 0 } и
- переходы соответствуют значениям, указанным в столбце (C) таблицы.
Например, дерево» 1 ( 1 ( 0 ( nil )))" принимается следующим запуском автомата дерева:
| С 0 ( | 1 ( | 1 ( | 0 ( | ноль | )))) | |||||
| ⇒ | 1 ( | С 1 ( | 1 ( | 0 ( | ноль | )))) | на 2 | |||
| ⇒ | 1 ( | 1 ( | С 0 ( | 0 ( | ноль | )))) | на 4 | |||
| ⇒ | 1 ( | 1 ( | 0 ( | С 0 ( | ноль | )))) | на 1 | |||
| ⇒ | 1 ( | 1 ( | 0 ( | ноль | ))) | на 0 |
Напротив, термин « 1 ( 0 ( nil ))" приводит к следующему непринятому запуску автомата:
| ⇒ С 0 ( | 1 ( | 0 ( | ноль | ))) | |||
| ⇒ | 1 ( | С 1 ( | 0 ( | ноль | )))) | на 2 | |
| ⇒ | 1 ( | 0 ( | С2 ( | ноль | )))) | на 3, дальнейшее правило не применимо |
Поскольку не существует других начальных состояний, кроме S 0, чтобы запустить работу автомата, термин " 1 ( 0 ( nil ))» не принимается древовидным автоматом.
В целях сравнения в столбцах (A) и (D) таблицы приведены (справа) регулярная (строковая) грамматика и регулярная древовидная грамматика соответственно, каждая из которых принимает тот же язык, что и ее автоматный аналог.
Свойства [ править ]
Узнаваемость [ править ]
Для восходящего автомата основной термин t (то есть дерево) принимается, если существует редукция, которая начинается с t и заканчивается q ( t ), где q — конечное состояние. Для нисходящего автомата основной термин t принимается, если существует сокращение, которое начинается с q ( t ) и заканчивается t , где q - начальное состояние.
Древовидный язык L ( A ) , принимаемый или распознаваемый древесным автоматом A, представляет собой набор всех основных термов, A. принимаемых Набор основных термов распознается , если существует древовидный автомат, который его принимает.
Линейный (т. е. сохраняющий арность) древесный гомоморфизм сохраняет распознаваемость. [7]
и сокращение Полнота
Недетерминированный конечный древесный автомат является полным , если существует хотя бы одно правило перехода, доступное для каждой возможной комбинации символа и состояний.Состояние q доступно , если существует основной терм t, такой, что существует редукция от t до q ( t ).Соглашение о свободной торговле сокращается, если все его государства доступны. [8]
Лемма о накачке [ править ]
Каждый достаточно большой [9] Основной термин t в узнаваемом древовидном языке L может быть вертикально трехдольным [10] такой, что произвольное повторение («накачка») средней части сохраняет результирующий член в L . [11] [12]
Для языка всех конечных списков логических значений из приведенного выше примера все термины, выходящие за пределы высоты k = 2, могут быть перекачаны, поскольку они должны содержать вхождение минусы . Например,
минусы ( ЛОЖЬ , минусы ( истинный , ноль ) ) , минусы ( ЛОЖЬ , минусы ( ЛОЖЬ , минусы ( истинный , ноль ) )) , минусы ( ЛОЖЬ , минусы ( ЛОЖЬ , минусы ( ЛОЖЬ , минусы ( истинный , ноль ) ))) , ...
все принадлежат этому языку.
Закрытие [ править ]
Класс узнаваемых древовидных языков замкнут относительно объединения, дополнения и пересечения. [13]
- Теорема Нерода Майхилла
Сравнение на множестве всех деревьев ранжированного алфавита — это отношение эквивалентности такое, что u 1 ≡ v 1 и ... и un ≡ v n F влечет f ( u 1 ,..., ) un ≡ f ( v 1 ,..., v n ) для любого f ∈ F .Он имеет конечный индекс, если число его классов эквивалентности конечно.
Для данного древовидного языка L сравнение может быть определено формулой u ≡ L v, если C [ u ] ∈ L ⇔ C [ v ] ∈ L для каждого контекста C .
Теорема Майхилла-Нерода для древесных автоматов утверждает, что следующие три утверждения эквивалентны: [14]
- L — узнаваемый древовидный язык
- L — объединение некоторых классов эквивалентности сравнения конечного индекса
- отношение ≡ L является конгруэнцией конечного индекса
См. также [ править ]
- Теорема Курселя - применение древесных автоматов для доказательства алгоритмической метатеоремы о графах
- Древовидные преобразователи — расширяют древовидные автоматы так же, как преобразователи слов расширяют словесные автоматы .
- Переменные древовидные автоматы
- Автоматы с бесконечным деревом
Примечания [ править ]
- ^ Коммон и др. 2008 г. , разд. 1.1, с. 20.
- ^ Коммон и др. 2008 г. , разд. 1.6, с. 38.
- ^ Коммон и др. 2008 г. , разд. 1.1, с. 23.
- ^ Комон и др. 2008 г. , разд. 1.6, теорема 1.6.1, с. 38.
- ^ В строгом смысле слова детерминированные нисходящие автоматы не определены Комоном и др. (2008), но там они используются (п. 1.6, предложение 1.6.2, с. 38). Они принимают класс языков деревьев с замкнутыми путями (раздел 1.8, упражнение 1.6, стр. 43-44).
- ^ Моравец, Фрэнк; Корнелл, Том (7 июля 1997 г.). «Представление ограничений с помощью автоматов» . Материалы 35-го ежегодного собрания Ассоциации компьютерной лингвистики и восьмой конференции европейского отделения Ассоциации компьютерной лингвистики . ACL '98/EACL '98. США: Ассоциация компьютерной лингвистики: 468–475. дои : 10.3115/976909.979677 .
- ^ Идея Comon et al. (2008 , разд. 1.4, теорема 1.4.3, стр. 31-32) гомоморфизма деревьев является более общим, чем теория из статьи «гомоморфизм деревьев».
- ^ Коммон и др. 2008 г. , разд. 1.1, с. 23-24.
- ^ Формально: высота ( t ) > k , где k > 0 зависит только от L , а не от t
- ^ Формально: существует контекст C [.], нетривиальный контекст C′ [.] и основной терм u такой, что t = C [ C′ [ u ]] . «Контекст» C [.] — это дерево с одной дыркой (или, соответственно, терм с одним вхождением одной переменной). Контекст называется «тривиальным», если дерево состоит только из дырочного узла (или, соответственно, если терм представляет собой всего лишь переменную). Обозначение C [ t ] означает результат вставки дерева t в дырку C [.] (или, соответственно, создания экземпляра переменной t ). Комон и др. 2008 , с. 17, дает формальное определение.
- ^ Формально: C [ C′ н [ u ]] ∈ L для всех n ≥ 0. Обозначение C н [.] означает результат объединения n копий C [.] одна в другую, ср. Комон и др. 2008 , с. 17.
- ^ Коммон и др. 2008 г. , разд. 1.2, с. 29.
- ^ Комон и др. 2008 г. , разд. 1.3, теорема 1.3.1, с. 30.
- ^ Коммон и др. 2008 г. , разд. 1.5, стр. 36.
Ссылки [ править ]
- Комон, Хьюберт; Доше, Макс; Жилерон, Реми; Жакмар, Флоран; Лужье, Денис; Лёдинг, Кристоф; Тисон, Софи; Томмаси, Марк (ноябрь 2008 г.). Техники и приложения древовидных автоматов . Проверено 11 февраля 2014 г.
- Хосоя, Харуо (4 ноября 2010 г.). Основы обработки XML: подход «дерево-автомат» . Издательство Кембриджского университета. ISBN 978-1-139-49236-2 .
- Гечег, Ференц; Стейнби, Магнус (1984). «Дерево автоматов». arXiv : 1509.06233 [ cs.FL ].
- Энгельфрит, Йост (1975). «Древовидные автоматы и древовидные грамматики». arXiv : 1510.02036 [ cs.FL ].
Внешние ссылки [ править ]
Реализации [ править ]
- Граппа — ранговые и неранжированные библиотеки древовидных автоматов (OCaml)
- Timbuk — инструменты для анализа достижимости и вычислений древовидных автоматов (OCaml)
- LETHAL — библиотека для работы с конечными деревьями и хедж-автоматами (Java)
- Библиотека древовидных автоматов с машинной проверкой (Isabelle [OCaml, SML, Haskell])
- VATA — библиотека для эффективного манипулирования недетерминированными древовидными автоматами (C++).