Логарифмический декремент

Логарифмический декремент можно получить, например, как ln( x ₁ / x ₃ ).

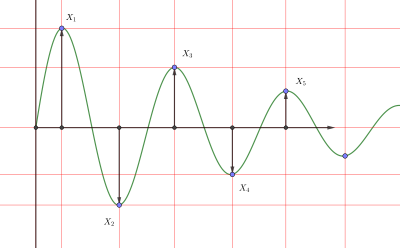
Логарифмический декремент , $\delta$, используется для определения коэффициента демпфирования системы с недостаточным демпфированием во временной области.

Метод логарифмического декремента становится все менее и менее точным по мере того, как коэффициент демпфирования увеличивается примерно до 0,5; это вообще не применимо к коэффициенту демпфирования больше 1,0, поскольку система имеет чрезмерное демпфирование .

Метод

Логарифмический декремент определяется как натуральный логарифм отношения амплитуд любых двух последовательных пиков:

$\delta ={\frac {1}{n}}\ln {\frac {x(t)}{x(t+nT)}}$

где x ( t ) — это выброс (амплитуда — конечное значение) в момент времени t, а x ( t + nT ) — это выброс пика на расстоянии n периодов, где n — любое целое число последовательных положительных пиков.

Затем коэффициент демпфирования находится по логарифмическому декременту по формуле:

$\zeta ={\frac {\delta }{\sqrt {4\pi ^{2}+\delta ^{2}}}}$

Таким образом, логарифмический декремент также позволяет оценить добротность системы :

$Q={\frac {1}{2\zeta }}$

$Q={\frac {1}{2}}{\sqrt {1+\left({\frac {n2\pi }{\ln {\frac {x(t)}{x(t+nT)}}}}\right)^{2}}}$

Затем коэффициент затухания можно использовать для нахождения собственной частоты ω _n вибрации системы по затухающей собственной частоте ω _d :

$\omega _{d}={\frac {2\pi }{T}}$

$\omega _{n}={\frac {\omega _{d}}{\sqrt {1-\zeta ^{2}}}}$

где T , период сигнала, представляет собой время между двумя последовательными пиками амплитуды недостаточно демпфированной системы.

Упрощенный вариант

Коэффициент затухания можно найти для любых двух соседних пиков. Этот метод используется, когда n = 1 , и является производным от общего метода, описанного выше:

$\zeta ={\frac {1}{\sqrt {1+\left({\frac {2\pi }{\ln \left({\frac {x_{0}}{x_{1}}}\right)}}\right)^{2}}}}$

где x ₀ и x ₁ — амплитуды любых двух последовательных пиков.

Для системы, где $\zeta \ll 1$ (не слишком близко к критически затухающему режиму, где $\zeta \approx 1$).

$\zeta \approx {\frac {\ln \left({\frac {x_{0}}{x_{1}}}\right)}{2\pi }}$

Метод дробного перерегулирования

Метод дробного перерегулирования может быть полезен для коэффициентов демпфирования примерно от 0,5 до 0,8. с дробным перерегулированием ОС :

$\mathrm {OS} ={\frac {x_{p}-x_{f}}{x_{f}}}$

где x _p — амплитуда первого пика переходного процесса, а x _f — амплитуда стабилизации. Тогда коэффициент демпфирования равен

$\zeta ={\frac {1}{\sqrt {1+\left({\frac {\pi }{\ln(\mathrm {OS} )}}\right)^{2}}}}$

См. также

• Коэффициент демпфирования

Ссылки

• Инман, Дэниел Дж. (2008). Инженерная вибрация . Аппер-Седл, Нью-Джерси: Pearson Education, Inc., стр. 43–48. ISBN  978-0-13-228173-7 .