Расширяемое хеширование

Расширяемое хеширование — это тип хеш- системы, которая рассматривает хэш как битовую строку и использует дерево для поиска в сегменте. ^[1] Из-за иерархической природы системы повторное хеширование является инкрементной операцией (выполняется по одному сегменту за раз, по мере необходимости). Это означает, что рост таблицы меньше влияет на чувствительные ко времени приложения, чем стандартное полное перехеширование таблицы.

Расширяемое хеширование было описано Рональдом Феджином в 1979 году. Практически все современные файловые системы используют либо расширяемое хеширование, либо B-деревья . В частности, Global File System , ZFS и SpadFS используют расширяемое хеширование. ^[2]

Пример

Предположим, что хеш-функция $h(k)$ возвращает строку битов. Первый $i$ биты каждой строки будут использоваться в качестве индексов, чтобы определить, куда они пойдут в «каталоге» (хеш-таблице), где $i$ — наименьшее число, при котором индекс каждого элемента таблицы уникален.

Ключи, которые будут использоваться:

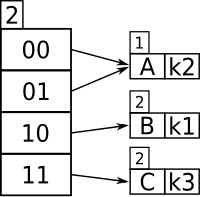
{\begin{aligned}h(k_{1})=100100\\h(k_{2})=010110\\h(k_{3})=110110\end{aligned}}

Предположим, что в этом конкретном примере размер сегмента равен 1. Первые два вставляемых ключа, k ₁ и k ₂ , можно отличить по старшему биту , и они будут вставлены в таблицу следующим образом:

Теперь, если бы k ₃ было хэшировано с таблицей, было бы недостаточно различать все три ключа по одному биту (потому что и k ₃ , и k ₁ имеют 1 в качестве крайнего левого бита). Кроме того, поскольку размер сегмента равен единице, таблица может переполниться. Поскольку сравнение первых двух старших битов дает каждому ключу уникальное местоположение, размер каталога удваивается следующим образом:

Итак, теперь k ₁ и k ₃ имеют уникальное местоположение, отличающееся первыми двумя крайними левыми битами. Поскольку k ₂ находится в верхней половине таблицы, на него указывают как 00, так и 01, поскольку нет другого ключа для сравнения, начинающегося с 0.

Приведенный выше пример взят из Fagin et al. (1979) .

Дополнительная информация

h(k_{4})=011110

Теперь необходимо вставить k ₄ , первые два бита которого равны 01..(1110), и при использовании глубины каталога в 2 бита это сопоставляется с 01 с сегментом A. Блок A заполнен (максимальный размер 1). ), поэтому его необходимо разделить; поскольку на сегмент A имеется более одного указателя, нет необходимости увеличивать размер каталога.

Необходима информация о:

Размер ключа, который отображает каталог (глобальная глубина), и
Размер ключа, который ранее сопоставил сегмент (локальная глубина).

Чтобы различать два случая действия:

Удвоение каталога при заполнении корзины
Создание новой корзины и перераспределение записей между старой и новой корзиной.

Рассматривая начальный случай расширяемой хеш-структуры, если каждая запись каталога указывает на один сегмент, то локальная глубина должна быть равна глобальной глубине.

Количество записей справочника равно 2 ^{глобальная глубина}, и начальное количество сегментов равно 2 ^{локальная глубина}.

Таким образом, если глобальная глубина = локальная глубина = 0, то 2 ⁰ = 1, поэтому начальный каталог содержит один указатель на одну корзину.

Вернёмся к двум случаям действий; если ведро полное:

Если локальная глубина равна глобальной глубине, то существует только один указатель на сегмент, и нет других указателей каталогов, которые могли бы сопоставиться с сегментом, поэтому каталог необходимо удвоить.
Если локальная глубина меньше глобальной глубины, то существует более одного указателя из каталога на сегмент, и сегмент можно разделить.

Ключ 01 указывает на сегмент A, а локальная глубина сегмента A, равная 1, меньше глобальной глубины каталога, равной 2, что означает, что ключи, хешированные для сегмента A, использовали только 1-битный префикс (т. е. 0), и сегмент должен иметь свой содержимое разделяется с помощью ключей длиной 1 + 1 = 2 бита; в общем, для любой локальной глубины d, где d меньше D, глобальная глубина, а затем d должна быть увеличена после разделения сегмента, а новый d используется как количество битов ключа каждой записи для перераспределения записей прежней ведро в новые ведра.

Сейчас,

h(k_{4})=011110

пробуется еще раз, с 2 битами 01.., и теперь ключ 01 указывает на новую корзину, но все еще есть ⁠ $k_{2}$ ⁠ в нем ( $h(k_{2})=010110$ и тоже начинается с 01).

Если ⁠ $k_{2}$ ⁠ был 000110, с ключом 00 проблем не было бы, потому что ⁠ $k_{2}$ ⁠ остался бы в новом ведре A', а ведро D было бы пустым.

(Это был бы наиболее вероятный случай, когда размер сегментов превышает 1, а переполнение вновь разделенных сегментов было бы крайне маловероятно, если только все записи не были снова объединены в один блок. Но просто чтобы подчеркнуть роль информацию о глубине, пример будет логически продолжен до конца.)

Таким образом, сегмент D необходимо разделить, но проверка его локальной глубины, равной 2, аналогична проверке глобальной глубины, равной 2, поэтому каталог необходимо разделить еще раз, чтобы хранить ключи с достаточной детализацией, например 3 бита.

Ведро D необходимо разделить, так как оно заполнено.
Поскольку локальная глубина D = глобальной глубине, каталог должен удвоиться, чтобы увеличить детализацию ключей.
Глобальная глубина увеличилась после разделения каталога на 3.
Новая запись ⁠ $k_{4}$ ⁠ переназначается с глобальной глубиной 3 бита и попадает в D, который имеет локальную глубину 2, которую теперь можно увеличить до 3, а D можно разделить на D' и E.
Содержимое разделенного ведра D, ⁠ $k_{2}$ ⁠ был перекодирован с использованием 3 битов и в итоге оказался в D'.
K4 повторяется и попадает в E, у которого есть свободный слот.

Сейчас, $h(k_{2})=010110$ находится в D и $h(k_{4})=011110$ пробуется еще раз, с 3 битами 011.., и он указывает на сегмент D, который уже содержит ⁠ $k_{2}$ ⁠ так полно; Локальная глубина D равна 2, но теперь глобальная глубина равна 3 после удвоения каталога, поэтому теперь D можно разделить на D' и E корзины, содержимое D, ⁠ $k_{2}$ ⁠ имеет свой $h(k_{2})$ повторная попытка с новой глобальной битовой маской глубины 3 и ⁠ $k_{2}$ ⁠ оказывается в D', затем появляется новая запись ⁠ $k_{4}$ ⁠ повторяется с $h(k_{4})$ побитовая маска с использованием нового количества битов глобальной глубины, равного 3, и это дает 011, что теперь указывает на новую корзину E, которая пуста. Итак ⁠ $k_{4}$ ⁠ попадает в ведро E.

Пример реализации

Ниже приведен расширяемый алгоритм хеширования на Python , в котором удалены проблемы ассоциации блока диска/страницы памяти, кэширования и согласованности. Обратите внимание, что проблема существует, если глубина превышает размер целого числа в битах, поскольку тогда удвоение каталога или разделение сегмента не позволит перехешировать записи в разные сегменты.

В коде используются младшие биты , что позволяет более эффективно расширять таблицу, поскольку весь каталог можно скопировать как один блок ( Ramakrishnan & Gehrke (2003) ).

Пример Python

PAGE_SZ = 10

class Page:
    def __init__(self) -> None:
        self.map = []
        self.local_depth = 0

    def full(self) -> bool:
        return len(self.map) >= PAGE_SZ

    def put(self, k, v) -> None:
        for i, (key, value) in enumerate(self.map):
            if key == k:
                del self.map[i]
                break
        self.map.append((k, v))

    def get(self, k):
        for key, value in self.map:
            if key == k:
                return value

    def get_local_high_bit(self):
      return 1 << self.local_depth

class ExtendibleHashing:
    def __init__(self) -> None:
        self.global_depth = 0
        self.directory = [Page()]

    def get_page(self, k):
        h = hash(k)
        return self.directory[h & ((1 << self.global_depth) - 1)]

    def put(self, k, v) -> None:
        p = self.get_page(k)
        full = p.full()
        p.put(k, v)
        if full:
            if p.local_depth == self.global_depth:
                self.directory *= 2
                self.global_depth += 1

            p0 = Page()
            p1 = Page()
            p0.local_depth = p1.local_depth = p.local_depth + 1
            high_bit = p.get_local_high_bit()
            for k2, v2 in p.map:
                h = hash(k2)
                new_p = p1 if h & high_bit else p0
                new_p.put(k2, v2)

            for i in range(hash(k) & (high_bit - 1), len(self.directory), high_bit):
                self.directory[i] = p1 if i & high_bit else p0
         
  
    def get(self, k):
        return self.get_page(k).get(k)

if __name__ == "__main__":
    eh = ExtendibleHashing()
    N = 10088
    l = list(range(N))

    import random
    random.shuffle(l)
    for x in l:
        eh.put(x, x)
    print(l)

    for i in range(N):
        print(eh.get(i))

Примечания

^ Феджин и др. (1979) .
^ Микулаш Паточка (2006). Проектирование и реализация файловой системы Spad (PDF) (Диссертация). Архивировано из оригинала (PDF) 15 марта 2016 г. Проверено 27 февраля 2016 г. «Раздел 4.1.6 Расширяемое хеширование: ZFS и GFS» и «Таблица 4.1: Организация каталогов в файловых системах»

См. также

Ссылки

Феджин, Р.; Нивергельт, Дж.; Пиппенджер, Н.; Стронг, HR (сентябрь 1979 г.), «Расширяемое хеширование — метод быстрого доступа к динамическим файлам», Транзакции ACM в системах баз данных , 4 (3): 315–344, doi : 10.1145/320083.320092 , S2CID 2723596
Рамакришнан, Р.; Герке, Дж. (2003), Системы управления базами данных, 3-е издание: Глава 11, Индексирование на основе хеша , стр. 373–378.
Зильбершац, Авраам ; Корт, Генри ; Сударшан, С., Концепции системы баз данных, шестое издание: глава 11.7, Динамическое хеширование

Внешние ссылки

В этой статье использованы общедоступные материалы из Пол Э. Блэк. «Расширяемое хеширование» . Словарь алгоритмов и структур данных . НИСТ .
Заметки о расширенном хешировании в Университете штата Арканзас
Расширяемые примечания к хешированию. Архивировано 3 марта 2016 г. на Wayback Machine.
Слайды из книги «Концепции системы базы данных», посвященные расширяемому хешированию для динамических индексов на основе хэша.

[FOOTNOTEFaginNievergeltPippengerStrong1979-1] Феджин и др. (1979) .

[2] Микулаш Паточка (2006). Проектирование и реализация файловой системы Spad (PDF) (Диссертация). Архивировано из оригинала (PDF) 15 марта 2016 г. Проверено 27 февраля 2016 г. «Раздел 4.1.6 Расширяемое хеширование: ZFS и GFS» и «Таблица 4.1: Организация каталогов в файловых системах»

[1]

[2]