Ближайший сосед с большой маржой

Ближайший сосед с большим запасом ( LMNN ) ^[1] Классификация — это статистический машинного обучения алгоритм для метрического обучения . Он изучает псевдометрику, предназначенную для классификации k-ближайших соседей . Алгоритм основан на полуопределенном программировании , подклассе выпуклой оптимизации .

Цель обучения с учителем (точнее, классификации) — изучить правило принятия решения, которое может классифицировать экземпляры данных по заранее определенным классам. Правило k-ближайшего соседа предполагает набор обучающих данных из помеченных экземпляров (т. е. классы известны). Он классифицирует новый экземпляр данных по классу, полученному большинством голосов k ближайших (помеченных) обучающих экземпляров. Близость измеряется с помощью заранее определенной метрики . Ближайшие соседи с большим запасом — это алгоритм, который изучает эту глобальную (псевдо)метрику контролируемым образом, чтобы повысить точность классификации правила k-ближайшего соседа.

Настраивать

Основная идея LMNN заключается в изучении псевдометрики, согласно которой все экземпляры данных в обучающем наборе окружены как минимум k экземплярами, имеющими одну и ту же метку класса. Если это достигнуто, ошибка исключения одного (особый случай перекрестной проверки ) сводится к минимуму. Пусть обучающие данные состоят из набора данных $D=\{({\vec {x}}_{1},y_{1}),\dots ,({\vec {x}}_{n},y_{n})\}\subset R^{d}\times C$ , где набор возможных категорий классов равен $C=\{1,\dots ,c\}$ .

Алгоритм изучает псевдометрику типа

d({\vec {x}}_{i},{\vec {x}}_{j})=({\vec {x}}_{i}-{\vec {x}}_{j})^{\top }\mathbf {M} ({\vec {x}}_{i}-{\vec {x}}_{j})

.

Для $d(\cdot ,\cdot )$ чтобы быть четко определенным, матрица $\mathbf {M}$ должно быть положительно полуопределенным . Евклидова метрика является частным случаем, когда $\mathbf {M}$ является единичной матрицей. Это обобщение часто (ошибочно) ^{[ нужна ссылка ]}), называемую метрикой Махаланобиса .

Рисунок 1 иллюстрирует влияние метрики при изменении $\mathbf {M}$ . Два круга показывают набор точек на равном расстоянии от центра. ${\vec {x}}_{i}$ . В евклидовом случае это множество представляет собой круг, тогда как в модифицированной метрике (Махаланобиса) оно становится эллипсоидом .

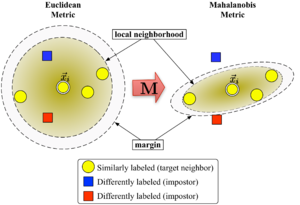
Рисунок 1: Схематическая иллюстрация LMNN.

Алгоритм различает два типа особых точек данных: целевые соседи и самозванцы .

Целевые соседи

Целевые соседи выбираются перед обучением. Каждый экземпляр ${\vec {x}}_{i}$ имеет точно $k$ разные целевые соседи внутри $D$ , которые имеют одну и ту же метку класса $y_{i}$ . Целевые соседи — это точки данных, которые должны стать ближайшими соседями по изученной метрике . Обозначим набор целевых соседей для точки данных ${\vec {x}}_{i}$ как $N_{i}$ .

Самозванцы

Самозванец точки данных ${\vec {x}}_{i}$ это еще одна точка данных ${\vec {x}}_{j}$ с другой меткой класса (т.е. $y_{i}\neq y_{j}$ ), который является одним из ближайших соседей ${\vec {x}}_{i}$ . Во время обучения алгоритм пытается минимизировать количество самозванцев для всех экземпляров данных в обучающем наборе.

Алгоритм

Большой запас ближайших соседей оптимизирует матрицу $\mathbf {M}$ с помощью полуопределенного программирования . Цель двоякая: для каждой точки данных ${\vec {x}}_{i}$ целевые соседи должны быть близко , а самозванцы должны быть далеко . На рисунке 1 показан эффект такой оптимизации на наглядном примере. Изученная метрика приводит к тому, что входной вектор ${\vec {x}}_{i}$ быть окружен обучающими экземплярами одного и того же класса. Если бы это была контрольная точка, она была бы правильно отнесена к категории $k=3$ правило ближайшего соседа.

Первая цель оптимизации достигается за счет минимизации среднего расстояния между экземплярами и их целевыми соседями.

\sum _{i,j\in N_{i}}d({\vec {x}}_{i},{\vec {x}}_{j})

.

Вторая цель достигается за счет штрафных санкций за расстояние до самозванцев. ${\vec {x}}_{l}$ которые находятся менее чем на одну единицу дальше, чем целевые соседи ${\vec {x}}_{j}$ (и, следовательно, выталкивая их из местного района ${\vec {x}}_{i}$ ). Результирующее значение, которое необходимо минимизировать, можно записать как:

\sum _{i,j\in N_{i},l,y_{l}\neq y_{i}}[d({\vec {x}}_{i},{\vec {x}}_{j})+1-d({\vec {x}}_{i},{\vec {x}}_{l})]_{+}

С потери шарнира функцией ${\textstyle [\cdot ]_{+}=\max(\cdot ,0)}$ , что гарантирует, что близость самозванца не будет наказываться за пределами поля. Запас ровно в одну единицу фиксирует масштаб матрицы. $M$ . Любой альтернативный выбор $c>0$ приведет к изменению масштаба $M$ в разы $1/c$ .

Окончательная задача оптимизации выглядит следующим образом:

\min _{\mathbf {M} }\sum _{i,j\in N_{i}}d({\vec {x}}_{i},{\vec {x}}_{j})+\lambda \sum _{i,j,l}\xi _{ijl}

\forall _{i,j\in N_{i},l,y_{l}\neq y_{i}}

d({\vec {x}}_{i},{\vec {x}}_{j})+1-d({\vec {x}}_{i},{\vec {x}}_{l})\leq \xi _{ijl}

\xi _{ijl}\geq 0

\mathbf {M} \succeq 0

Гиперпараметр ${\textstyle \lambda >0}$ — некоторая положительная константа (обычно устанавливается посредством перекрестной проверки). Здесь переменные $\xi _{ijl}$ (вместе с двумя типами ограничений) заменяет член в функции стоимости. Они играют роль, аналогичную резервным переменным, поглощая степень нарушений ограничений самозванца. Последнее ограничение гарантирует, что $\mathbf {M}$ является положительно полуопределенным. Задача оптимизации является примером полуопределенного программирования (SDP). Хотя SDP, как правило, страдают от высокой вычислительной сложности, этот конкретный экземпляр SDP может быть решен очень эффективно благодаря основным геометрическим свойствам проблемы. В частности, большинство ограничений-самозванцев естественным образом удовлетворяются и их не нужно применять во время выполнения (т. е. набор переменных $\xi _{ijl}$ является редким). Особенно хорошо подходящим методом решателя является метод рабочего набора , который сохраняет небольшой набор активно применяемых ограничений и лишь изредка отслеживает оставшиеся (вероятно удовлетворяемые) ограничения, чтобы гарантировать правильность.

Расширения и эффективные решатели

В статье 2008 года LMNN был расширен на несколько локальных показателей. ^[2] Это расширение значительно уменьшает ошибку классификации, но требует более дорогостоящей задачи оптимизации. В своей публикации 2009 года в Журнале исследований машинного обучения ^[3] Вайнбергер и Сол нашли эффективный решатель для полуопределенной программы. Он может изучить метрику для набора рукописных цифр MNIST за несколько часов, включая миллиарды парных ограничений. Реализация с открытым исходным кодом Matlab находится в свободном доступе на веб-странице авторов .

Кумаль и др. ^[4] расширил алгоритм, включив локальные инварианты в многомерные полиномиальные преобразования и улучшенную регуляризацию.

См. также

Ссылки

^ Вайнбергер, КК; Блитцер Дж.К.; Саул Л.К. (2006). «Дистанционное метрическое обучение для классификации ближайших соседей с большим запасом» . Достижения в области нейронных систем обработки информации . 18 : 1473–1480.
^ Вайнбергер, КК; Саул Л.К. (2008). «Быстрые решатели и эффективные реализации дистанционного обучения метрикам» (PDF) . Материалы международной конференции по машинному обучению : 1160–1167. Архивировано из оригинала (PDF) 24 июля 2011 г. Проверено 14 июля 2010 г.
^ Вайнбергер, КК; Саул Л.К. (2009). «Дистанционное метрическое обучение для классификации с большой маржой» (PDF) . Журнал исследований машинного обучения . 10 : 207–244.
^ Кумар, член парламента; Торр PHS; Зиссерман А. (2007). «Инвариантный классификатор ближайших соседей с большим запасом». 2007 г. 11-я Международная конференция IEEE по компьютерному зрению . стр. 1–8. дои : 10.1109/ICCV.2007.4409041 . ISBN 978-1-4244-1630-1 . S2CID 1326101 .

Внешние ссылки

[Weinberger05-1] Вайнбергер, КК; Блитцер Дж.К.; Саул Л.К. (2006). «Дистанционное метрическое обучение для классификации ближайших соседей с большим запасом» . Достижения в области нейронных систем обработки информации . 18 : 1473–1480.

[Weinberger08-2] Вайнбергер, КК; Саул Л.К. (2008). «Быстрые решатели и эффективные реализации дистанционного обучения метрикам» (PDF) . Материалы международной конференции по машинному обучению : 1160–1167. Архивировано из оригинала (PDF) 24 июля 2011 г. Проверено 14 июля 2010 г.

[Weinberger09-3] Вайнбергер, КК; Саул Л.К. (2009). «Дистанционное метрическое обучение для классификации с большой маржой» (PDF) . Журнал исследований машинного обучения . 10 : 207–244.

[kumar07-4] Кумар, член парламента; Торр PHS; Зиссерман А. (2007). «Инвариантный классификатор ближайших соседей с большим запасом». 2007 г. 11-я Международная конференция IEEE по компьютерному зрению . стр. 1–8. дои : 10.1109/ICCV.2007.4409041 . ISBN 978-1-4244-1630-1 . S2CID 1326101 .

[1]

[2]

[3]

[4]