Зенер-пиннинг

Закрепление Зенера – это влияние дисперсии мелких частиц на движение малоугловых и большеугловых границ зерен через поликристаллический материал. Маленькие частицы предотвращают движение таких границ, оказывая закрепляющее давление , которое противодействует движущей силе, толкающей границы. Закрепление Зенера очень важно при обработке материалов, поскольку оно оказывает сильное влияние на восстановление , рекристаллизацию и рост зерна .

Происхождение силы закрепления

Граница представляет собой несовершенство кристаллической структуры и как таковая связана с определенным количеством энергии . Когда граница проходит через некогерентную частицу, часть границы, которая находилась бы внутри частицы, по существу перестает существовать. Чтобы пройти мимо частицы, необходимо создать какую-то новую границу, а это энергетически невыгодно. Пока область границы рядом с частицей закреплена, остальная часть границы продолжает пытаться двигаться вперед под действием собственной движущей силы. Это приводит к тому, что граница между теми точками, где она прикреплена к частицам, искривляется.

Математическое описание

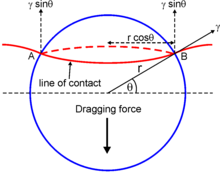
На рисунке изображена граница, пересекающаяся с некогерентной частицей радиуса $r$ . Сила закрепления действует вдоль линии контакта границы с частицей, т. е. по окружности диаметром $AB=2\pi r\cos \theta$ . Сила на единицу длины контактирующей границы равна $\gamma \sin \theta$ , где $\gamma$ это межфазная энергия . Следовательно, полная сила, действующая на границу раздела частица-граница, равна

F=2\pi r\gamma \cos \theta \sin \theta

Максимальная сдерживающая сила возникает, когда $\theta =45^{\circ }$ , так $F_{max}=\pi r\gamma$ .

Чтобы определить силу закрепления, возникающую в результате заданной дисперсии частиц, Кларенс Зинер сделал несколько важных предположений:

Частицы имеют сферическую форму .
Прохождение границы не меняет взаимодействия частицы с границей.
Каждая частица оказывает максимальную силу закрепления на границе независимо от положения контакта.
Контакты между частицами и границами совершенно случайны.
Плотность частиц на границе соответствует ожидаемой при случайном распределении частиц.

Для объемной доли, $F_{v}$ , из случайно распределенных сферических частиц радиуса $r$ , количество частиц в единице объема (плотность числа) определяется выражением

N_{total}={\frac {3F_{v}}{4\pi r^{3}}}.

Только частицы в пределах одного радиуса (сплошные кружки) могут пересекать плоскую границу.

Из этой общей плотности числа только те частицы, которые находятся в пределах одного радиуса частицы, смогут взаимодействовать с границей. Если граница по существу плоская , то эта дробь будет равна

N_{interact}=2rN_{total}={\frac {3F_{v}}{2\pi \ r^{2}}}.

Учитывая предположение, что все частицы прикладывают максимальную силу закрепления, $F_{max}$ , общее давление пиннинга, оказываемое распределением частиц на единицу площади границы, равно

P_{s}=N_{interact}F_{max}={\frac {3F_{v}\gamma \ }{2r}}.\,\!

Это называется давлением закрепления Зенера. Отсюда следует, что большие давления закрепления создаются за счет:

Увеличение объемной доли частиц
Уменьшение размера частиц

Давление закрепления Зинера зависит от ориентации, а это означает, что точное давление закрепления зависит от степени когерентности на границах зерен. ^[1]

Компьютерное моделирование

Закрепление частиц широко изучалось с помощью компьютерного моделирования, такого как методы Монте-Карло и методы фазового поля . Эти методы могут фиксировать интерфейсы сложной формы и обеспечивать лучшее приближение силы закрепления.

Взаимодействие частицы и границы раздела с использованием модели фазового поля.

Примечания

Согласно «Текущие проблемы рекристаллизации: обзор» , RD Doherty et al., Materials Science and Engineering A238 (1997), стр. 219-274.
Для получения информации о моделировании стабилитрона см.:

- «Вклад в изучение динамики пиннинга Зенера: численное моделирование методом конечных элементов», диссертация на французском языке (2003 г.). Г. Кутюрье.
- «3D конечно-элементное моделирование торможения нормального роста зерен частицами». Acta Materialia, 53, стр. 977–989 (2005). Г. Кутюрье, Р. Доэрти, Кл. Морис, Р. Фортунье.
- «3D конечно-элементное моделирование динамики пиннинга Зенера». Философский журнал, том 83, № 30, стр. 3387–3405 (2003). Г. Кутюрье, Кл. Морис, Р. Фортунье.