Двумерный граф
В теории графов двумерный граф — это граф, множество вершин которого можно разделить на две равные части так, что каждая вершина смежна ровно с одной вершиной из другого множества, не содержащего ее. [1] [2] [3] В двумерном графе G с 2 n вершинами существует множество из n независимых ребер, такое что ни одно нечетное число из них не лежит на цикле G .
Примеры
[ редактировать ]Граф Петерсена , показанный ниже, представляет собой двумерный граф: если разбить его на внешний пятиугольник и внутреннюю пятиконечную звезду, каждая вершина на одной стороне разбиения будет иметь ровно одного соседа на другой стороне разбиения. В более общем плане то же самое верно для любого обобщенного графа Петерсена, образованного путем соединения внешнего многоугольника и внутренней звезды с одинаковым количеством точек; например, это относится к графу Мёбиуса-Кантора и графу Дезарга .

Любой граф гиперкуба , такой как четырехмерный гиперкуб, показанный ниже, также является двумерным.

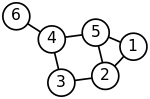
Однако график, показанный ниже, не является двумерным. Какие бы три независимых ребра вы ни выбрали, одно из них является ребром цикла.
Двуцветные деревья
[ редактировать ]Дерево T с 2 n вершинами является двумерным тогда и только тогда, когда число независимости T n равно идеальное или, что то же самое, тогда и только тогда, когда оно имеет паросочетание . [1]
Обобщения
[ редактировать ], k -вариантный граф k ≥ 3, можно определить аналогично. Граф называется k -варигатированным, если его множество вершин можно разбить на k равных частей так, что каждая вершина смежна ровно с одной вершиной из любой другой части, не содержащей ее. [2]
Примечания
[ редактировать ]- Характеристика последовательностей степеней двумерных графов была нерешенной проблемой теории графов.
Ссылки
[ редактировать ]- Беднарек, Арканзас; Сандерс, Э. Л. (1973), «Характеристика двумерных деревьев», Discrete Mathematics , 5 : 1–14, doi : 10.1016/0012-365X(73)90022-8 .
- Бхат-Наяк, Васанти Н .; Чоудум, Южная Каролина ; Наик, Ранджан Н. (1978), «Характеристика 2-мерных графов и 3-мерных графов», Discrete Mathematics , 23 : 17–22, doi : 10.1016/0012-365X(78)90182-6 .
- Бхат-Наяк, Васанти Н .; Кочай, Вашингтон ; Наик, Ранджан Н. (1980), «Принудительно 2-мерные последовательности степеней», Utilitas Math. , 18 : 83–89 .
- Бхат-Наяк Васанти Н. , Ранджан Н. Найк, Дополнительные результаты о 2-мерных графах, Utilitas Math. 12 (1977) 317–325.
- Джавдекар, Медха (1980), «Характеристика принудительно k -переменных последовательностей степеней, k ≥ 3», Discrete Mathematics , 29 (1): 33–38, doi : 10.1016/0012-365X(90)90284-O .
- Джавдекар, Медха (1980), «Характеристика k -разнообразных графов, k ≥ 3», Discrete Mathematics , 32 (3): 263–270, doi : 10.1016/0012-365X(80)90264-2
- Риддл, Фэй А. (1978), Двумерные графы и их изоморфизмы , доктор философии. диссертация, Университет Флориды .