Граф Дезарга
| Граф Дезарга | |
|---|---|
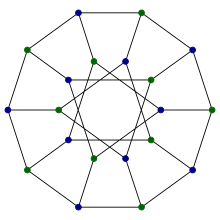 | |
| Назван в честь | Жерар Дезарг |
| Вершины | 20 |
| Края | 30 |
| Радиус | 5 |
| Диаметр | 5 |
| Обхват | 6 |
| Автоморфизмы | 240 ( С 5 × С 2 ) |
| Хроматическое число | 2 |
| Хроматический индекс | 3 |
| Род | 2 |
| Толщина книги | 3 |
| Номер очереди | 2 |
| Характеристики | Кубический Дистанционно-регулярный гамильтониан двусторонний Симметричный |
| Таблица графиков и параметров | |
В математической области теории графов граф Дезарга представляет собой дистанционно-транзитивный кубический граф с 20 вершинами и 30 ребрами. [1] Он назван в честь Жирара Дезарга , возникает из нескольких различных комбинаторных конструкций, имеет высокий уровень симметрии, является единственным известным неплоским кубическим частичным кубом и применялся в химических базах данных.
Название «граф Дезарга» также использовалось для обозначения графа с десятью вершинами, дополнения графа Петерсена , который также может быть сформирован как двудольная половина графа Дезарга с 20 вершинами. [2]
Конструкции
[ редактировать ]Существует несколько различных способов построения графа Дезарга:
- Это обобщенный граф Петерсена G (10,3) . Чтобы таким образом сформировать граф Дезарга, соедините десять вершин в правильный десятиугольник , а остальные десять вершин соедините в десятиконечную звезду, соединяющую пары вершин на расстоянии три во втором десятиугольнике. Граф Дезарга состоит из 20 ребер этих двух многоугольников вместе с дополнительными 10 ребрами, соединяющими точки одного десятиугольника с соответствующими точками другого.
- Это граф Леви конфигурации Дезарга . Эта конфигурация состоит из десяти точек и десяти линий, описывающих два перспективных треугольника , их центр перспективы и ось перспективы. Граф Дезарга имеет одну вершину для каждой точки, одну вершину для каждой прямой и одно ребро для каждой пары инцидентных точек и линий. Теорема Дезарга , названная в честь французского математика 17-го века Жерара Дезарга , описывает набор точек и линий, образующих эту конфигурацию, а конфигурация и график получили свое название от нее.
- Это двудольное двойное покрытие графа Петерсена , образованное заменой каждой вершины графа Петерсена парой вершин и каждого ребра графа Петерсена парой скрещенных ребер.
- Это двудольный граф Кнезера H 5,2 . Его вершины могут быть помечены десятью двухэлементными подмножествами и десятью трехэлементными подмножествами пятиэлементного набора с ребром, соединяющим две вершины, когда одно из соответствующих наборов является подмножеством другого. Эквивалентно, граф Дезарга — это индуцированный подграф 5-мерного гиперкуба, определяемый вершинами веса 2 и веса 3.
- Граф Дезарга является гамильтоновым и может быть построен с использованием обозначений LCF : [5,−5,9,−9] 5 . Поскольку Эрдеш предположил, что при k > 0 подграф (2 k + 1) -мерного гиперкуба, индуцированный вершинами веса k и k + 1, является гамильтоновым, гамильтоновость графа Дезарга не является неожиданностью. (Из более сильной гипотезы Ловаса также следует, что, за исключением нескольких известных контрпримеров, все вершинно-транзитивные графы имеют гамильтоновы циклы.)
Алгебраические свойства
[ редактировать ]Граф Дезарга является симметричным графом : он обладает симметриями, которые переводят любую вершину в любую другую вершину и любое ребро в любое другое ребро. Его группа симметрии имеет порядок 240 и изоморфна произведению симметрической группы в 5 точках с группой порядка 2.
Это произведение представления группы симметрии можно интерпретировать в терминах конструкции графа Дезарга: симметричная группа на пяти точках является группой симметрии конфигурации Дезарга, а подгруппа порядка 2 меняет роли вершин, представляющих точки. конфигурации Дезарга и вершин, представляющих линии. Альтернативно, в терминах двудольного графа Кнезера , симметричная группа на пяти точках действует отдельно на двухэлементное и трехэлементное подмножества пяти точек, а дополнение подмножеств образует группу второго порядка, которая преобразует один тип подмножества в другой. Симметричная группа на пяти точках также является группой симметрии графа Петерсена , а подгруппа порядка 2 меняет местами вершины внутри каждой пары вершин, образованной в конструкции двойного покрытия.
Обобщенный граф Петерсена G ( n , k ) вершинно -транзитивен тогда и только тогда, когда n = 10 и k = 2 или если k 2 ≡ ±1 (mod n ) и является транзитивным по ребру только в следующих семи случаях: ( n , k ) = (4, 1) , (5, 2) , (8, 3) , (10, 2) , ( 10, 3) , (12, 5) , (24, 5) . [3] Таким образом, граф Дезарга — один из семи симметричных обобщенных графов Петерсена. Среди этих семи графов — кубический граф G (4, 1) , граф Петерсена G (5, 2) , граф Мёбиуса–Кантора G (8, 3) , додекаэдрический граф G (10, 2) и граф Науру . Г (12, 5) .
Характеристический полином графа Дезарга есть
Следовательно, граф Дезарга является целым графом : его спектр полностью состоит из целых чисел.
Приложения
[ редактировать ]В химии граф Дезарга известен как граф Дезарга-Леви ; его используют для организации систем стереоизомеров 5- лигандных соединений. В этом приложении тридцать ребер графа соответствуют псевдовращениям лигандов. [4] [5]
Другие объекты недвижимости
[ редактировать ]Граф Дезарга имеет прямолинейный номер пересечения 6 и является наименьшим кубическим графом с этим номером пересечения (последовательность A110507 в OEIS ). Это единственный известный неплоский кубический частичный куб . [6]
Граф Дезарга имеет хроматическое число 2, хроматический индекс 3, радиус 5, диаметр 5 и обхват 6. Это также 3 -связный по вершинам и 3 -связный по ребрам гамильтонов граф . Имеет толщину книги 3 и номер очереди 2. [7]
Все кубически- дистанционно-регулярные графы известны. [8] Граф Дезарга — один из 13 таких графов.
Граф Дезарга можно вложить как самодвойственное Петри регулярное отображение в неориентируемое многообразие рода 6 с десятиугольными гранями. [9]
Галерея
[ редактировать ]- График Дезарга раскрашен для выделения различных циклов.
- Хроматический индекс графа Дезарга равен 3.
- Хроматическое число графа Дезарга равно 2.
Ссылки
[ редактировать ]- ^ Вайсштейн, Эрик В. , «График Дезарга» , MathWorld
- ^ Каньо, И.Н. (1947), «Графы Дезарга и Паппа и их группы», American Journal of Mathematics , 69 (4), The Johns Hopkins University Press: 859–863, doi : 10.2307/2371806 , JSTOR 2371806 .
- ^ Фрухт, Р .; Грейвер, Дж. Э.; Уоткинс, М.Э. (1971), «Группы обобщенных графов Петерсена», Proceedings of the Cambridge Philosophical Society , 70 (2): 211–218, Bibcode : 1971PCPS...70..211F , doi : 10.1017/S0305004100049811 , S2CID 122686848 .
- ^ Балабан, АТ; Фуркашиу, Д.; Буник, Р. (1966), «Графики множественных 1, 2-сдвигов в ионах карбония и родственных системах», преподобный Рум. Хим. , 11 : 1205
- ^ Мислоу, Курт (1970), «Роль псевдовращения в стереохимии реакций нуклеофильного замещения», Acc. хим. Рез. , 3 (10): 321–331, doi : 10.1021/ar50034a001
- ^ Клавжар, Санди; Липовец, Аленка (2003), «Частичные кубы как графы подразделения и как обобщенные графы Петерсена», Discrete Mathematics , 263 (1–3): 157–165, doi : 10.1016/S0012-365X(02)00575-7
- ^ Вольц, Джессика, Разработка линейных макетов с помощью SAT. Магистерская диссертация, Тюбингенский университет, 2018 г.
- ^ Брауэр, AE ; Коэн, AM; и Ноймайер А. Дистанционно-регулярные графы. Нью-Йорк: Springer-Verlag, 1989.
- ^ МакМаллен, Питер (1992), «Правильные многогранники типа { p ,3} с 2 p вершинами», Geometricae Dedicata , 43 (3), doi : 10.1007/BF00151518 , ISSN 0046-5755



