Алгоритм построения фильтра Паркса – Макклеллана

Полосы пропускания и задерживания фильтра, построенного по алгоритму Паркса – Макклеллана.
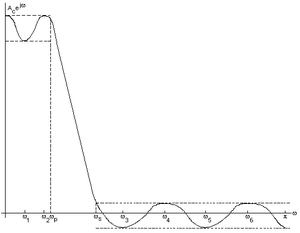
Ось y представляет собой частотную характеристику H (ω), а ось x представляет собой различные частоты в радианах ω _i . Можно отметить, что две частоты отмечены на оси x, ω _p и ω _s . ω _p указывает частоту среза полосы пропускания, а ω _s указывает частоту среза полосы пропускания. График в виде пульсации в левом верхнем углу — это пульсация полосы пропускания, а пульсация в правом нижнем углу — пульсация полосы задерживания. Две пунктирные линии в левом верхнем углу графика обозначают δ _p , а две пунктирные линии в правом нижнем углу обозначают δ _s . Все остальные перечисленные частоты указывают на экстремальные частоты графика частотной характеристики. В результате имеется шесть экстремальных частот, а затем мы добавляем частоты полосы пропускания и полосы задерживания, чтобы получить в общей сложности восемь экстремальных частот на графике.

Алгоритм Паркса-Макклеллана , опубликованный Джеймсом Макклелланом и Томасом Парксом в 1972 году, представляет собой итерационный алгоритм для поиска оптимального с конечной импульсной характеристикой (FIR) фильтра Чебышева . Алгоритм Паркса-Макклеллана используется для разработки и реализации эффективных и оптимальных КИХ-фильтров. Он использует косвенный метод поиска оптимальных коэффициентов фильтра.

Цель алгоритма — минимизировать ошибку в полосах пропускания и заграждения за счет использования аппроксимации Чебышева. Алгоритм Паркса-Макклеллана является разновидностью алгоритма обмена Ремеза с той разницей, что он специально разработан для КИХ-фильтров. Это стало стандартным методом проектирования КИХ-фильтров.

История

История создания оптимального КИХ-фильтра

В 1960-х годах исследователи в области проектирования аналоговых фильтров использовали приближение Чебышева для проектирования фильтров. В то время было хорошо известно, что лучшие фильтры имеют равноравномерную характеристику по величине своей частотной характеристики, а эллиптический фильтр (или фильтр Кауэра) является оптимальным с точки зрения приближения Чебышева. Когда в 1960-х годах началась революция цифровых фильтров, исследователи использовали билинейное преобразование для создания цифровых эллиптических фильтров с бесконечной импульсной характеристикой (БИХ). Они также осознали потенциал разработки КИХ-фильтров для выполнения той же задачи фильтрации, и вскоре начался поиск оптимального КИХ-фильтра с использованием аппроксимации Чебышева.

Как в математике, так и в технике было хорошо известно, что оптимальная реакция будет проявлять равноравномерное поведение и что количество пульсаций можно подсчитать с помощью приближения Чебышева. В период с 1962 по 1971 год было предпринято несколько попыток разработать программу проектирования оптимального КИХ-фильтра Чебышева. Несмотря на многочисленные попытки, большинство из них не увенчались успехом, обычно из-за проблем в алгоритмической реализации или формулировке задачи. Отто Херрманн, например, предложил метод разработки равнополосных фильтров с ограниченными краями полос. Этот метод позволил получить равно пульсирующую частотную характеристику с максимальным количеством пульсаций путем решения набора нелинейных уравнений. Другой метод, представленный в то время, реализовал оптимальное приближение Чебышева, но алгоритм был ограничен разработкой фильтров относительно низкого порядка.

Подобно методу Херрманна, Эд Хофстеттер представил алгоритм, позволяющий создавать КИХ-фильтры с максимально возможным количеством пульсаций. Это стало известно как алгоритм максимальной пульсации. Алгоритм максимальной пульсации вводил условие попеременной ошибки посредством интерполяции, а затем решал набор уравнений, которым должно было удовлетворять попеременное решение. Одним из заметных ограничений алгоритма максимальной пульсации было то, что края полосы не задавались в качестве входных данных для процедуры проектирования. Скорее, исходный набор частот { ω _i } и желаемая функция D ( ω _i ) неявно определяли полосу пропускания и задержки. В отличие от предыдущих попыток разработать оптимальный фильтр, алгоритм максимальной пульсации использовал метод обмена, который пытался найти набор частот { ω _i }, где лучший фильтр имел пульсации. Таким образом, алгоритм максимальной пульсации не был оптимальной конструкцией фильтра, но он оказал весьма существенное влияние на формулировку алгоритма Паркса-Макклеллана.

История парков – Макклеллан

В августе 1970 года Джеймс Макклеллан поступил в аспирантуру Университета Райса по специальности математические модели проектирования аналоговых фильтров и записался на новый курс под названием «Цифровые фильтры» из-за его интереса к проектированию фильтров. Курс вели совместно Томас Паркс и Сид Беррус . В то время DSP была развивающейся областью, и в результате в лекциях часто использовались недавно опубликованные исследовательские работы. В следующем семестре, весной 1971 года, Томас Паркс предложил курс под названием «Теория сигналов», который Макклеллан тоже прослушал. Во время весенних каникул в семестре Паркс поехал из Хьюстона в Принстон, чтобы присутствовать на конференции, где он услышал презентацию Эда Хофстеттера о новом алгоритме разработки КИХ-фильтра (алгоритме максимальной пульсации). Он привез статью Хофстеттера, Оппенгейма и Зигеля обратно в Хьюстон, размышляя о возможности использования теории аппроксимации Чебышева для разработки КИХ-фильтров. Он услышал, что метод, реализованный в алгоритме Хофстеттера, аналогичен алгоритму обмена Ремеза, и решил пойти по пути использования алгоритма обмена Ремеза. Студенты курса «Теория сигналов» должны были выполнить проект, и, поскольку аппроксимация Чебышева была основной темой курса, реализация этого нового алгоритма стала курсовым проектом Джеймса Макклеллана. В конечном итоге это привело к созданию алгоритма Паркса – Макклеллана, который включал теорию оптимального приближения Чебышева и эффективную реализацию. К концу весеннего семестра Макклеллан и Паркс пытались написать вариант алгоритма обмена Ремеза для КИХ-фильтров. Разработка заняла около шести недель, и к концу мая некоторые оптимальные фильтры были успешно разработаны.

Алгоритм

Алгоритм Паркса – Макклеллана реализуется с использованием следующих шагов:

1. Инициализация: выберите экстремальный набор частот {ω _i ⁽⁰⁾ }.
2. Приближение конечного множества: вычислите лучшее приближение Чебышева на текущем экстремальном множестве, дав значение δ. ^(м) для минимальной-максимальной ошибки на данном экстремальном наборе.
3. Интерполяция: вычислите функцию ошибок E(ω) по всему набору частот Ω, используя (2).
4. Ищите локальные максимумы | Э ^(м) (о) | на съемочной площадке Ох.
5. Если макс _(ωεΩ) | Э ^(м) (о) | > д ^(м) , затем обновите экстремальный набор до { ω _i ^(м+1) } выбирая новые частоты, где | Э ^(м) (ω) | имеет свои локальные максимумы. Убедитесь, что ошибка чередуется на упорядоченном наборе частот, как описано в (4) и (5). Вернитесь к шагу 2 и выполните итерацию.
6. Если макс _(ωεΩ) | Э ^(м) (о) | ≤ d ^(м) , то алгоритм завершен. Используйте набор {ω _i ⁽⁰⁾ } и формула интерполяции для вычисления обратного дискретного преобразования Фурье для получения коэффициентов фильтра.

Алгоритм Паркса – Макклеллана можно переформулировать в виде следующих шагов:

1. Сделайте первоначальное предположение об экстремальных частотах L+2.
2. Вычислите δ, используя приведенное уравнение.
3. Используя интерполяцию Лагранжа, мы вычисляем плотный набор выборок A (ω) в полосе пропускания и полосе задерживания.
4. Определите новые самые большие экстремумы L+2.
5. Если теорема об чередовании не выполняется, то мы возвращаемся к (2) и итерируем до тех пор, пока теорема об чередовании не будет удовлетворена.
6. Если теорема об чередовании удовлетворена, мы вычисляем h(n) и все готово.

Чтобы получить общее представление об упомянутом выше алгоритме Паркса – Макклеллана, мы можем переписать приведенный выше алгоритм в более простой форме:

1. Угадайте, что положения экстремумов равномерно распределены в полосе пропускания и задержки.
2. Выполните полиномиальную интерполяцию и переоцените положения локальных экстремумов.
3. Перемещайте экстремумы на новые позиции и повторяйте действия до тех пор, пока экстремумы не перестанут смещаться.

Объяснение

На рисунке выше справа показаны различные экстремальные частоты для показанного графика. Экстремальные частоты — это максимальные и минимальные точки в полосах остановки и пропускания. Неравномерность полосы задерживания — это нижняя часть пульсаций в правом нижнем углу графика, а пульсация полосы пропускания — это верхняя часть пульсаций в левом верхнем углу графика. Пунктирные линии, пересекающие график, обозначают δ или максимальную ошибку. Учитывая положения экстремальных частот, существует формула оптимального δ или оптимальной ошибки. Поскольку мы не знаем оптимума δ или точного положения экстремумов с первой попытки, мы выполняем итерацию. По сути, мы изначально предполагаем положение экстремумов и вычисляем δ. Затем мы переоцениваем и перемещаем экстремумы и пересчитываем δ, или ошибку. Мы повторяем этот процесс до тех пор, пока δ не перестанет меняться. Алгоритм приведет к сходимости ошибки δ, обычно в течение десяти-двенадцати итераций.

Дополнительные примечания

Прежде чем применить приближение Чебышева, необходимо было выполнить ряд шагов:

1. Определите набор базисной функции для аппроксимации и
2. Используйте тот факт, что полосы пропускания и заграждения полосовых фильтров всегда будут разделены переходными областями.

Поскольку КИХ-фильтры можно свести к случаю суммы косинусов, одну и ту же базовую программу можно использовать для выполнения всех возможных КИХ-фильтров с линейной фазой. В отличие от подхода с максимальной пульсацией, края полос теперь можно было указать заранее.

Чтобы добиться эффективной реализации оптимальной конструкции фильтра с использованием алгоритма Паркса-Макклеллана, необходимо преодолеть две трудности:

1. Определение гибкой стратегии обмена и
2. Реализация надежного метода интерполяции.

В некотором смысле программирование включало реализацию и адаптацию известного алгоритма для использования при разработке КИХ-фильтра. Чтобы сделать программу более эффективной, были использованы две стороны стратегии обмена:

1. Распределение экстремальных частот между полосами пропускания и заграждения и
2. Включение перемещения экстремалей между полосами по мере выполнения программы.

При инициализации количество экстремалей в полосах пропускания и заграждения можно было задать, используя соотношение размеров полос. Более того, края полос пропускания и заграждения всегда будут помещены в экстремальный набор, а логика программы удерживает эти граничные частоты в экстремальном наборе. Перемещение между полосами контролировалось путем сравнения размера ошибок на всех кандидатных экстремальных частотах и ​​выбора наибольшей. Вторым элементом алгоритма был шаг интерполяции, необходимый для оценки функции ошибок. Они использовали метод, называемый барицентрической формой интерполяции Лагранжа, который оказался очень надежным.

Все условия алгоритма Паркса – Макклеллана основаны на теореме Чебышева об альтернировании. Теорема об альтернировании утверждает, что полином степени L, минимизирующий максимальную ошибку, будет иметь не менее L+2 экстремумов. Оптимальная частотная характеристика едва достигает пределов максимальной пульсации. Экстремумы должны возникать на краях полос пропускания и заграждения и либо при ω=0, либо при ω=π, либо при обоих. Производная многочлена степени L — это многочлен степени L−1, который может быть равен нулю не более чем в L−1 местах. Таким образом, максимальное количество локальных экстремумов — это L−1 локальных экстремумов плюс 4 края полосы, что в сумме дает L+3 экстремума.

Дополнительные ссылки

Следующие дополнительные ссылки предоставляют информацию об алгоритме Паркса-Макклеллана, а также о других исследованиях и статьях, написанных Джеймсом Макклелланом и Томасом Парксом:

1. Приближение Чебышева для нерекурсивных цифровых фильтров с линейной фазой
2. Краткая справка по проектированию КИХ-фильтров нижних частот Паркса – Макклеллана с использованием MATLAB
3. Введение в ЦСП
4. Документация MathWorks MATLAB
5. Конспекты лекций ELEC4600 ( исходная ссылка , архивировано 15 апреля 2012 г.)
6. Реализация кода C (лицензия LGPL) – Джейк Яновец
7. Программное обеспечение Айова-Хиллз. «Пример кода C» . Проверено 3 мая 2014 г.
8. Пересмотренный и расширенный алгоритм Макклеллан, Паркс и Рабинер, 1975; Код Фортрана.