декодер Витерби

Декодер Витерби использует алгоритм Витерби для декодирования битового потока, который былкодируется с помощью сверточного кода или решетчатого кода .

Существуют и другие алгоритмы декодирования сверточно-кодированного потока (например, алгоритм Фано ). Алгоритм Витерби является самым ресурсоемким, но он выполняет декодирование максимального правдоподобия . Чаще всего он используется для декодирования сверточных кодов с длиной ограничения k≤3, но на практике используются значения до k=15.

Декодирование Витерби было разработано Эндрю Дж. Витерби и опубликовано в статье. Витерби, А. (апрель 1967 г.). «Границы ошибок для сверточных кодов и асимптотически оптимальный алгоритм декодирования». Транзакции IEEE по теории информации . 13 (2): 260–269. дои : 10.1109/тит.1967.1054010 .

Существуют как аппаратные (в модемах), так и программные реализации декодера Витерби.

Декодирование Витерби используется в итеративном алгоритме декодирования Витерби .

Аппаратная реализация

Аппаратный декодер Витерби базового (неперкированного) кода обычно состоит из следующих основных блоков:

Отраслевая метрическая единица (БМУ)
Единица измерения пути (PMU)
Блок обратной связи (TBU)

Отраслевая метрическая единица (БМУ)

Функция единицы метрики ветвления заключается в вычислении метрики ветвления , которая представляет собой нормированные расстояния между всеми возможными символами в кодовом алфавите и полученным символом.

Существуют декодеры Витерби с жестким и мягким решением. Декодер Витерби с жестким решением получает на вход простой битовый поток, а расстояние Хэмминга в качестве метрики используется . Декодер Витерби с мягким решением получает битовый поток, содержащий информацию о достоверности каждого полученного символа. Например, в 3-битном кодировании эта информация о надежности может быть закодирована следующим образом:

ценить	значение
000	сильнейший	0
001	относительно сильный	0
010	относительно слабый	0
011	самый слабый	0
100	самый слабый	1
101	относительно слабый	1
110	относительно сильный	1
111	сильнейший	1

Конечно, это не единственный способ кодирования данных о надежности.

Квадрат . евклидова расстояния используется в качестве метрики для декодеров мягкого решения

Единица измерения пути (PMU)

Блок метрики пути суммирует метрики ветвей, чтобы получить метрики для $2^{K-1}$ путей, где K — длина ограничения кода, один из которых в конечном итоге может быть выбран как оптимальный . Каждые часы, которые он делает $2^{K-1}$ решения, отбрасывая заведомо неоптимальные пути. Результаты этих решений записываются в память блока трассировки.

Основными элементами PMU являются блоки ACS (Add-Compare-Select) . Способ их связи между собой определяется решетчатой диаграммой конкретного кода .

Поскольку метрики ветвей всегда $\geq 0$ , должна быть дополнительная схема (не показана на изображении), предотвращающая переполнение счетчиков метрик. Альтернативный метод, который устраняет необходимость отслеживать рост метрик пути, состоит в том, чтобы позволить метрикам пути «переворачиваться»; Чтобы использовать этот метод, необходимо убедиться, что аккумуляторы метрик пути содержат достаточно бит, чтобы предотвратить попадание «лучших» и «худших» значений в пределах 2. ^(n-1) друг друга. Схема сравнения практически не изменилась.

Можно отслеживать уровень шума во входящем потоке битов, отслеживая скорость роста метрики «лучшего» пути. Более простой способ сделать это — отслеживать одно местоположение или «состояние» и наблюдать, как оно проходит «вверх», скажем, через четыре дискретных уровня в пределах диапазона аккумулятора. По мере прохождения вверх через каждый из этих порогов счетчик увеличивается, что отражает «шум», присутствующий во входящем сигнале.

Блок обратной связи (TBU)

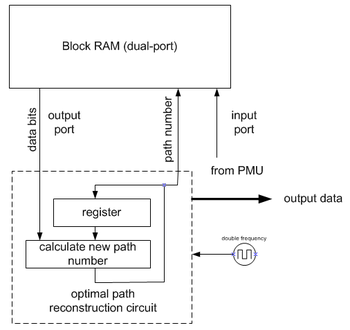
Модуль обратной трассировки восстанавливает путь (почти) максимального правдоподобия на основе решений, принятых PMU. Поскольку он делает это в обратном направлении, декодер Витерби содержит буфер FILO (первый пришел последним) для восстановления правильного порядка.

Обратите внимание, что реализация, показанная на изображении, требует двойной частоты. Есть несколько хитростей, которые устраняют это требование.

Проблемы реализации

Квантование для декодирования мягкого решения

Чтобы в полной мере воспользоваться преимуществами декодирования с мягким решением, необходимо правильно квантовать входной сигнал. Оптимальная ширина зоны квантования определяется по следующей формуле:

\,\!T={\sqrt {\frac {N_{0}}{2^{k}}}},

где $N_{0}$ — спектральная плотность мощности шума, а k — количество бит для мягкого решения.

Вычисление евклидовой метрики

Квадрат нормы ( $\ell _{2}$ ) расстояние между полученными и фактическими символами в кодовом алфавите может быть дополнительно упрощено до линейной формы суммы/разности, что делает его менее трудоемким в вычислениях.

1/2 Рассмотрим сверточный код , который генерирует 2 бита ( 00 , 01 , 10 или 11 ) для каждого входного бита ( 1 или 0 ). Эти сигналы возврата к нулю переводятся в форму без возврата к нулю, показанную рядом.

кодовый алфавит	векторное картографирование
00	+1, +1
01	+1, −1
10	−1, +1
11	−1, −1

Каждый принятый символ может быть представлен в векторной форме как v _r = {r ₀ , r ₁ }, где r ₀ и r ₁ - значения мягкого решения, величины которых означают совместную надежность принятого вектора v _r .

Аналогичным образом каждый символ кодового алфавита может быть представлен вектором v _i = {±1, ±1}.

Фактическое вычисление метрики евклидова расстояния выглядит следующим образом:

\,\!D=({\overrightarrow {v_{r}}}-{\overrightarrow {v_{i}}})^{2}={\overrightarrow {v_{r}}}^{2}-2{\overrightarrow {v_{r}}}{\overrightarrow {v_{i}}}+{\overrightarrow {v_{i}}}^{2}

Каждый квадратный термин представляет собой нормированное расстояние, отражающее энергию символа. Например, энергия символа v _i = {±1, ±1} может быть вычислена как

\,\!{\overrightarrow {v_{i}}}^{2}=(\pm 1)^{2}+(\pm 1)^{2}=2

Таким образом, энергетический терм всех символов в кодовом алфавите постоянен (при ( нормированном ) значении 2).

Операция Add-Compare-Select ( ACS ) сравнивает метрическое расстояние между принятыми символами ||v _r || и любые два символа кодового алфавита, пути которых сливаются в узле соответствующей решетки, ||v _i⁽⁰⁾|| и ||v _я⁽¹⁾|| . Это эквивалентно сравнению

\,\!D_{0}={\overrightarrow {v_{r}}}^{2}-2{\overrightarrow {v_{r}}}{\overrightarrow {v_{i}^{0}}}+{\overrightarrow {v_{i}^{0}}}^{2}

и

\,\!D_{1}={\overrightarrow {v_{r}}}^{2}-2{\overrightarrow {v_{r}}}{\overrightarrow {v_{i}^{1}}}+{\overrightarrow {v_{i}^{1}}}^{2}

Но из вышесказанного мы знаем, что энергия v i _. нормированному) значению 2), а энергия v постоянна (равна ( _r одинакова в обоих случаях Это сводит сравнение к функции минимума между двумя (средними) членами скалярного произведения :

\,\!\min(-2{\overrightarrow {v_{r}}}{\overrightarrow {v_{i}^{0}}},-2{\overrightarrow {v_{r}}}{\overrightarrow {v_{i}^{1}}})=\max({\overrightarrow {v_{r}}}{\overrightarrow {v_{i}^{0}}},{\overrightarrow {v_{r}}}{\overrightarrow {v_{i}^{1}}})

поскольку $операция min$ над отрицательными числами может интерпретироваться как эквивалентная $операция max$ над положительными величинами.

Каждый термин скалярного произведения может быть расширен как

\,\!\max(\pm r_{0}\pm r_{1},\pm r_{0}\pm r_{1})

где знаки каждого слагаемого зависят от символов, v _i⁽⁰⁾ и ви _я⁽¹⁾, сравнивается. Таким образом, вычисление квадрата расстояния евклидовой метрики для вычисления метрики ветвления может быть выполнено с помощью простой операции сложения/вычитания.

обратная трассировка

Общий подход к обратной трассировке состоит в том, чтобы накопить метрики пути до пятикратной длины ограничения (5 ( K - 1)), найти узел с наибольшей накопленной стоимостью и начать обратную трассировку с этого узла.

Обычно используемое практическое правило, согласно которому глубина усечения в пять раз превышает объем памяти (длина ограничения K -1) сверточного кода, является точным только для кодов со скоростью 1/2. Для произвольной скорости точным эмпирическим правилом является 2,5( K - 1)/(1− r ), где r — скорость кода. ^[1]

Однако вычисление узла, накопившего наибольшую стоимость (наибольшую или наименьшую целочисленную метрику пути), включает в себя нахождение максимумов или минимумов нескольких (обычно 2 ^{К -1}) числа, что может занять много времени при реализации во встроенных аппаратных системах.

Большинство систем связи используют декодирование Витерби, включающее пакеты данных фиксированных размеров с фиксированным шаблоном битов / байтов либо в начале, либо в конце пакета данных. Используя известный бит / байтовый шаблон в качестве ссылки, начальному узлу можно установить фиксированное значение, тем самым получая идеальный путь максимального правдоподобия во время обратной трассировки.

Ограничения

Физическая реализация декодера Витерби не даст точного потока максимального правдоподобия из-за квантования входного сигнала, метрик ветвей и путей, а также конечной длины обратной трассировки . Практические реализации приближаются к идеалу в пределах 1 дБ.

На выходе декодера Витерби при декодировании сообщения, поврежденного аддитивным гауссовским каналом, имеются ошибки, сгруппированные в пакеты ошибок. ^[2]^[3]Коды, исправляющие одиночные ошибки, сами по себе не могут исправить такие пакеты, поэтому либо сверточный код и декодер Витерби должны быть разработаны достаточно мощными, чтобы снизить количество ошибок до приемлемого уровня, либо коды, исправляющие пакетные ошибки необходимо использовать .

Проколотые коды

Аппаратный декодер Витерби выколотых кодов обычно реализуется следующим образом:

Депунктурер, который преобразует входной поток в поток, который выглядит как исходный (непроколотый) поток с метками ERASE в местах, где биты были стерты.
Базовый декодер Витерби, понимающий эти метки ERASE (то есть не использующий их для расчета метрики ветвей).

Программная реализация

Одной из наиболее трудоемких операций является ACS-бабочка, которая обычно реализуется с использованием языка ассемблера и соответствующих расширений набора команд (таких как SSE2 ) для ускорения времени декодирования.

Приложения

Алгоритм декодирования Витерби широко используется в следующих областях:

Радиосвязь: цифровое телевидение ( ATSC , QAM , DVB-T и др.), радиореле , спутниковая связь , цифровой режим PSK31 для радиолюбительства .
Декодирование решетчато-кодированной модуляции (TCM) - метода, используемого в модемах телефонных линий для достижения высокой спектральной эффективности аналоговых телефонных линий с полосой пропускания 3 кГц.
Компьютерные устройства хранения данных, такие как жесткие диски .
Автоматическое распознавание речи

Ссылки

^ Б. Мойсион, «Практическое правило глубины усечения для сверточных кодов», Семинар по теории информации и приложениям, 2008 г., Сан-Диего, Калифорния, 2008 г., стр. 555-557, два : 10.1109/ITA.2008.4601052 .
^ Стефан Хост, Рольф Йоханнессон, Дмитрий К. Зигангирод, Камил Ш. Зигангирод и Виктор Васильевич Зяблод. «О распределении длин выходных пакетов ошибок при декодировании Витерби сверточных кодов» .
^ Карри, С.Дж.; Хармон, Вашингтон «Ограничение длины пакета ошибок декодера Витерби» .

Внешние ссылки

Форни, Дж. Дэвид-младший (29 апреля 2005 г.). «Алгоритм Витерби: личная история». arXiv : cs/0504020 .
Подробности о расшифровке Витерби, а также библиография .
Объяснение алгоритма Витерби с акцентом на вопросы аппаратной реализации .
r =1/6 k =15 кодирование миссии Кассини на Сатурн .
Онлайн-генератор оптимизированного программного обеспечения декодеров Витерби (GPL) .
Программное обеспечение декодера GPL Viterbi для четырех стандартных кодов .
Описание декодера Витерби с k =24, который считается самым крупным из когда-либо применявшихся на практике .
Общее аппаратное обеспечение декодера Витерби (GPL) .

[1] Б. Мойсион, «Практическое правило глубины усечения для сверточных кодов», Семинар по теории информации и приложениям, 2008 г., Сан-Диего, Калифорния, 2008 г., стр. 555-557, два : 10.1109/ITA.2008.4601052 .

[2] Стефан Хост, Рольф Йоханнессон, Дмитрий К. Зигангирод, Камил Ш. Зигангирод и Виктор Васильевич Зяблод. «О распределении длин выходных пакетов ошибок при декодировании Витерби сверточных кодов» .

[3] Карри, С.Дж.; Хармон, Вашингтон «Ограничение длины пакета ошибок декодера Витерби» .

[1]

[2]

[3]