Звездная раскраска

Звездчатое хроматическое число графа Дейка равно 4, а хроматическое число — 2.

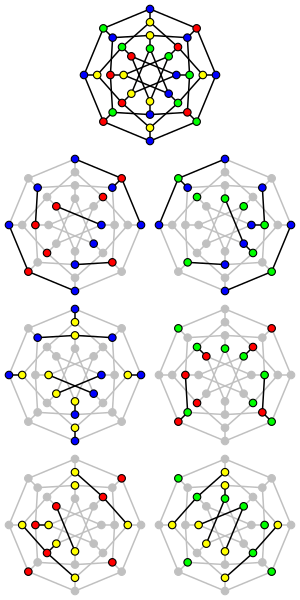
В математической области теории графов звездная раскраска графа G . — это (правильная) раскраска вершин , в которой каждый путь на четырех вершинах использует как минимум три различных цвета Аналогично, в звездной раскраске индуцированные подграфы, образованные вершинами любых двух цветов, имеют связные компоненты , которые являются звездными графами . Раскраска звезд была введена Грюнбаумом (1973) .Звездное хроматическое число ⁠ $\chi _{s}(G)$⁠ из G — это наименьшее количество цветов, необходимых для звездного G. цвета

Одним из обобщений звездной раскраски является тесно связанная концепция ациклической раскраски , где требуется, чтобы в каждом цикле использовалось как минимум три цвета, поэтому двухцветные индуцированные подграфы представляют собой леса . Если мы обозначим ациклическое хроматическое число графа G через ⁠ $\chi _{a}(G)$⁠ , у нас есть это ⁠ $\chi _{a}(G)\leq \chi _{s}(G)$⁠ , и на самом деле каждая звездная раскраска G является ациклической раскраской.

доказали, что звездное хроматическое число ограничено в каждом собственном минорном закрытом классе Нешетржил и Оссона де Мендес (2003) . Эти результаты были дополнительно обобщены Нешетрилом и Оссона де Мендес (2006) на все раскраски с малой глубиной дерева (стандартная раскраска и раскраска звезды представляют собой раскраски с малой глубиной дерева с соответствующими параметрами 1 и 2).

Сложность

Это было продемонстрировано Альбертсоном и др. (2004) что NP-полно определить, является ли $\chi _{s}(G)\leq 3$, даже если G графом является одновременно плоским и двудольным . Коулман и Море (1984) показали, что найти оптимальную раскраску звезды NP-трудно, даже если G — двудольный граф.

Ссылки

• Альбертсон, Майкл О.; Чаппелл, Гленн Г.; Кирстед, Хэл А.; Кюндген, Андре; Рамамурти, Радхика (2004), «Раскраска без двухцветных P ₄ » , Электронный журнал комбинаторики , 11 (1), doi : 10.37236/1779 , MR   2056078 .
• Коулман, Томас Ф .; Море, Хорхе (1984), «Оценка разреженных матриц Гессе и задачи раскраски графов» (PDF) , Mathematical Programming , 28 (3): 243–270, doi : 10.1007/BF02612334 , hdl : 1813/6374 , MR   0736293 .
• Фертен, Гийом; Распо, Андре; Рид, Брюс (2004), «Звездная раскраска графов» , Журнал теории графов , 47 (3): 163–182, doi : 10.1002/jgt.20029 , MR   2089462 .
• Грюнбаум, Бранко (1973), «Ациклические раскраски плоских графов», Израильский математический журнал , 14 (4): 390–408, doi : 10.1007/BF02764716 , MR   0317982 .
• Нешетржил, Ярослав ; Оссона де Мендес, Патрис (2003), «Раскраски и гомоморфизмы второстепенных замкнутых классов», Дискретная и вычислительная геометрия: Фестиваль Гудмана-Поллака , Алгоритмы и комбинаторика, том. 25, Springer-Verlag, стр. 651–664, MR   2038495 .
• Нешетржил, Ярослав ; Оссона де Мендес, Патрис (2006), «Глубина дерева, раскраска подграфов и границы гомоморфизма», European Journal of Combinatorics , 27 (6): 1022–1041, doi : 10.1016/j.ejc.2005.01.010 , MR   2226435 .

Внешние ссылки

• Раскраски звезд и ациклические раскраски (1973) , представленные на семинаре «Исследовательский опыт для аспирантов» (REGS) в Университете Иллинойса, 2008.