Граф Дика

Граф Дика
Граф Дика
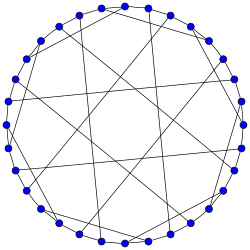	Граф Дейка
Назван в честь	В. Дайк
Вершины	32
Края	48
Радиус	5
Диаметр	5
Обхват	6
Автоморфизмы	192
Хроматическое число	2
Хроматический индекс	3
Толщина книги	3
Номер очереди	2
Характеристики	Симметричный ; Кубический ; гамильтониан ; двусторонний ; Граф Кэли
	Таблица графиков и параметров

В математической области теории графов граф Дейка — это 3- регулярный граф с 32 вершинами и 48 ребрами, названный в честь Вальтера фон Дейка . ^[1]^[2]

Это гамильтониан со 120 различными гамильтоновыми циклами. Он имеет хроматическое число 2, хроматический индекс 3, радиус 5, диаметр 5 и обхват 6. Это также 3- вершинно-связный и 3- реберно-связный граф. Имеет толщину книги 3 и номер очереди 2. ^[3]

Граф Дика является тороидальным графом ; двойственным к его симметричному тороидальному вложению является граф Шрикханде .

Алгебраические свойства

Группа автоморфизмов графа Дика — это группа порядка 192. ^[4] Он действует транзитивно на вершинах, ребрах и дугах графа. Следовательно, граф Дика является симметричным графом . Он имеет автоморфизмы, которые переводят любую вершину в любую другую вершину и любое ребро в любое другое ребро. Согласно переписи Фостера , граф Дайка, обозначаемый как F32A, является единственным кубически-симметричным графом с 32 вершинами. ^[5]

Характеристический полином графа Дика равен $(x-3)(x-1)^{9}(x+1)^{9}(x+3)(x^{2}-5)^{6}$ .

Карта Дейка

Граф Дайка представляет собой скелет симметричной мозаики поверхности рода три на двенадцать восьмиугольников, известной как карта Дика или мозаика Дика . Двойственный граф для этого разбиения представляет собой полный трехдольный граф K _4,4,4 . ^[6]^[7]

Галерея

Альтернативный рисунок графа Дика.
Хроматическое число графа Дика равно 2.
графа Хроматический индекс Дика равен 3.

Ссылки

^ Дайк, В. (1881), «Об установлении и исследовании группы и иррациональности регулярных римановых поверхностей» , Ann. , 17 (4): 473, doi : 10.1007/bf01446929 , S2CID 122956853 .
^ Вайсштейн, Эрик В. «График Дайка» . Математический мир .
^ Вольц, Джессика; Проектирование линейных макетов с помощью SAT. Магистерская диссертация, Тюбингенский университет, 2018 г.
^ «GG» , Энциклопедия графиков , получено 26 февраля 2024 г.
^ Кондер, М .; Добчаньи, П. (2002), «Трехвалентные симметричные графы до 768 вершин», Дж. Комбин. Математика. Комбинировать. Вычислить. , 40 : 41–63 .
^ Дайк, В. (1880), «Замечание о регулярной римановой поверхности пола 3 и связанной с ней нормальной кривой 4-го порядка» , Ann. , 17 : 510–516, doi : 10.1007/bf01446930 , S2CID 121904710 .
^ Сеулеманс, А. (2004), «Тетракисоктаэдрическая группа графа Дайка и ее молекулярная реализация», Molecular Physics , 102 (11): 1149–1163, doi : 10.1080/00268970410001728780 , S2CID 97973403 .

[1] Дайк, В. (1881), «Об установлении и исследовании группы и иррациональности регулярных римановых поверхностей» , Ann. , 17 (4): 473, doi : 10.1007/bf01446929 , S2CID 122956853 .

[2] Вайсштейн, Эрик В. «График Дайка» . Математический мир .

[3] Вольц, Джессика; Проектирование линейных макетов с помощью SAT. Магистерская диссертация, Тюбингенский университет, 2018 г.

[4] «GG» , Энциклопедия графиков , получено 26 февраля 2024 г.

[5] Кондер, М .; Добчаньи, П. (2002), «Трехвалентные симметричные графы до 768 вершин», Дж. Комбин. Математика. Комбинировать. Вычислить. , 40 : 41–63 .

[6] Дайк, В. (1880), «Замечание о регулярной римановой поверхности пола 3 и связанной с ней нормальной кривой 4-го порядка» , Ann. , 17 : 510–516, doi : 10.1007/bf01446930 , S2CID 121904710 .

[7] Сеулеманс, А. (2004), «Тетракисоктаэдрическая группа графа Дайка и ее молекулярная реализация», Molecular Physics , 102 (11): 1149–1163, doi : 10.1080/00268970410001728780 , S2CID 97973403 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]